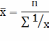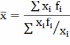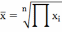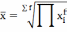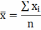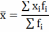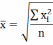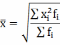- •1. Предмет статистической науки и задачи статистики на современном этапе.
- •2. Статистическая совокупность, ее виды. Единицы совокупности и классификация их признаков.
- •3. Метод статистики и основные этапы статистического исследования.
- •4. Организация статистики в рб. Источники и способы получения статистической информации.
- •6. Программно-методологические вопросы плана статистического наблюдения.
- •10. Погрешности (ошибки) стат.Наблюдения. Методы проверки дорстоверности статистических данных
- •11. Сводка – вторая стадия статистического исследования. Её задачи, программа, план и техника.
- •12. Понятие о группировке, её задачи и виды
- •13.Методологические вопросы построения группировки
- •14. Важнейшие группировки и классификации применяемые в статистике.
- •15. Ряды распределения, их виды и графическое изображение.
- •16.Статистические таблицы, их виды и осн правила построения.
- •17.Статистические показатели и их классификация.
- •18.Абсолютные статистические величины, их виды, значение и единицы измерения.
- •19. Относительные величины и область их применения. Способы их расчета и формы выражения.
- •20. Виды относительных величин.
- •21. Понятие о статистическом графике, его основные элементы и правила построения.
- •22. Виды статистических графиков и область их применения.
- •23. Сущность и значение средних величин. Основные научные положения теории средних. Определяющее свойство средней.
- •24. Средняя арифметическая, ее основные математические свойства и методы расчета.
- •25. Средняя гармоническая и другие виды средних. Обусловленность выбора средней характером исходной информации.
- •26. Мода и медиана, их смысл и значение в социально-экономических исследованиях, способы вычисления.
- •27. Статистическое изучение вариации. Показатели вариации и методы их расчета.
- •28. Дисперсия, ее математические свойства и методы расчета.
- •29. Дисперсия альтернативного признака.
- •30. Виды дисперсий и правило сложения дисперсий.
- •31. Коэффициент детерминации и эмпирическое корреляционное отношение как показатели тесноты связи между факторами по аналитической группировке.
- •32. Сущность выборочного наблюдения и его теоретические основы.
- •33. Виды и способы отбора единиц в выборочную совокупность.
- •34. Ошибки выборки и методы их расчета по среднему значению выборочного показателя и по доле признака выборочной совокупности.
- •35. Определение необходимой численности (объема) выборки.
- •36. Способы распространения результатов выборочного наблюдения на генеральную совокупность. Практика применения выборочных исследований в статистике.
- •37. Понятие о рядах динамики, их виды и правила построения.
- •38. Аналитические показатели динамического ряда, способы их расчета и взаимосвязь.
- •39. Средние показатели динамического ряда и методы их расчета.
- •40. Понятие тенденции ряда динамики и основные методы ее выявления (укрупнение интервалов, способ скользящей средней).
- •42. Сезонные колебания и методы их изучения.
- •43. Сущность индексов, задачи, решаемые индексным методом и классификация индексов.
- •44. Индивидуальные и общие (сводные) индексы. Принципы построения систем взаимосвязанных агрегатных индексов.
- •45. Средние индексы и их виды
- •46. Индексный метод анализа динамики среднего уровня (индексы переменного, постоянного состава и структурных сдвигов).
- •47. Ряды индексов с постоянной и переменной базами сравнения, с постоянными и переменными весами, их взаимосвязь.
- •48. Взаимосвязи индексов.
- •49. Принципы постр.Многофакт.Индексов
- •50. Территор.Индексы
- •52. Статистические методы изучения связей: метод сравнения параллельных рядов, метод аналитических группировок, графический метод, балансовый метод.
- •55. Понятие о множественной корреляции.
- •54. Понятие криволинейной зависимости, оценка тесноты связи при криволинейной зависимости.
24. Средняя арифметическая, ее основные математические свойства и методы расчета.
С редняя
арифмет-я бывает простой
и взвешенной.
Если данные осредняемого признака
представлены в несгруппир-м
виде
(как индив-ые значения первичного
признака у отд-х единиц совок-ти), то в
этом случае средняя рассчит-ся по
формуле средней
арифмет-й простой х=∑х/n,
где х-среднее значение признака; х-
индив-е значения признака у каждой
единицы совок-ти; n-число
единиц совок-ти. Если исходные данные
пред-ны в сгруппир-м
виде,
т.е. в виде рядов распр-ния (дискретных
и интервальных), то средняя величина в
таких случаях рассчит-ся по формуле
средней
ариф-кой взвешенной х=∑хf/∑f,
где х-варианты значений осредняемого
признака; f-
частоты (веса) для каждого из вариантов
признака, показывающие их повторяемость.
редняя
арифмет-я бывает простой
и взвешенной.
Если данные осредняемого признака
представлены в несгруппир-м
виде
(как индив-ые значения первичного
признака у отд-х единиц совок-ти), то в
этом случае средняя рассчит-ся по
формуле средней
арифмет-й простой х=∑х/n,
где х-среднее значение признака; х-
индив-е значения признака у каждой
единицы совок-ти; n-число
единиц совок-ти. Если исходные данные
пред-ны в сгруппир-м
виде,
т.е. в виде рядов распр-ния (дискретных
и интервальных), то средняя величина в
таких случаях рассчит-ся по формуле
средней
ариф-кой взвешенной х=∑хf/∑f,
где х-варианты значений осредняемого
признака; f-
частоты (веса) для каждого из вариантов
признака, показывающие их повторяемость.
Р ассмотрим свойства средней арифм-кой. Для уяснения сущности и упрощения расчетов средней арифм-кой величины используются след. основные свойства.
1. Среднее от постоянной равно ей самой; 2. Увеличение или уменьшение одной и той же величины приводит к изменению средней на ту же величину.3. Умножение/деление каждого варианта в А раз изменяет среднюю во столько же раз.4. Изменение каждого из весов в одно и тоже количество раз не изменяет величины среднего показателя. 5. Алгебраическая сумма отклонений всех вариантов от средней арифметической равно 0; 6. Среднее от суммы или разности нескольких величин равно сумме средних значений этих величин. 7. Сумма квадратов отклонений от средней арифметической меньше, чем от любой другой величины. При наличии всех индивидуальных или сгруппированных значений признака X, полученных в результате стат. наблюдения применяют формулу простой средней или взвешенной средней. При определении средней арифм-кой в интервальном ряду распределения осущ-тся в 2 этапа: 1. Рассч-ся середина каждого интервала, которая принимается за новое значение х, при этом для открытых интервалов их ширина условно принимается равной ширине соседних или смежных интервалов; 2. Далее рассчитывается средняя арифм-кая величина по формуле взвешенной средней.
25. Средняя гармоническая и другие виды средних. Обусловленность выбора средней характером исходной информации.
Средняя вел-на – показатель, выр-щий хар-ные свойственные большенству признаков, размеры и соотношения. Она бывает простая и взвешанная. Осн. виды вел-н: 1)ср. арифметическая;2) ср. гармоническая;3)ср. геометрическая;4)ср. квадратическая и др. Ср. арифметическая самая распространенная. Простая применяется, когда варианта встречается 1 раз или одинаковое число раз, а если не одинаковое число раз, то взвешанная.Скорость течения любого процесса находится в обратном отношении к общему времени этого процесса. Т.о. ср. гармоническая – средняя из обратных значений осредняемого признака или обратная вел-на ср. арифметической. Она применяется, когда статистическая инф-ция не содержит значений частот по отдельным вариантам совокупности, а представлена как их произведение. В обычном случае рассчитывают простую ср. гармоническую – среднюю из обратных значений признака и исп-ся, когда значение частоты неизвестно, но если известен ряд вариант (Х) и ряд произведений в ряд на частоту (х*f), а сама частота не известна, то средняя рассчитывается по формуле ср. гармонич. взвешенной. При решении ряда задач иногда возникает необходимость вычисления и др. ср. вел-н.
Наименование средней |
Формулы расчета |
|
простая |
взвешенная |
|
Ср. гармоническая |
|
|
Средняя геометрическая |
|
|
Средняя арифметическая |
|
|
Средняя квадратическая |
|
|
Где n-кол-во ед-ц совокупности, f-частота повторяемости индивид.значений признака, х-индивид.значение признака у каждой ед-цы совокупности, П-произведение.