
4. Кинематикалық талдау
Манипулятор кинематикалық талдау - серпiннiң зерттеуiне содан соң өтуге рұқсат беретiн техникалық жүйелердi робот бастапқы жобалау кезең және манипуляторлардың жүрiстi басқарудың синтезiне. Осы мақсатта нысананы көздейтiн қозғалысты механика түзу шешiмдi жорию және кинематика керi есеп, жағдайын анықтамасында қосылады және манипулятор жалпыланған координата бұл берiлген мән оның жағдай бiрмәндi анықтайтын механикалық жүйеде бойымен координаттар жүйе таңдалған бағыт схватасы. Тура есеп шешiм әрқашан бiрмәндi және манипулятор құрайтын буындарды кез-келген сан үшiн мүмкiн алыну. Қармау берiлген күй бойымен мағыналарын анықтамасында жалпыланған координата тұрады.
Жалпы бұл мiндетті жағдай бiрмәндi болып көрiнбейдi. Мысалы, осылай, жазық екi звенолы тетiгi үшiн манипуляторға тән нүкте қармау берiлген жағдайда iске асыратын екi кескiндi анықтауға болады, осы уақытта қимылдық дәреже саны артық алты бар көп түйiндi манипулятор үшiн жалпыланған координата таңдалған мағыналарына артық сәйкес келген шешiмдердi көптi аламыз.
4.1. Негiзгi өзгертулер
Манипулятор көпбуынды механизм қозғалыс тiзбек ажыратылған құрастыратын абсолюттi қатты денелдердi жүйенi сияқты қаралады. Әр мұндай жеке буын таныстырылатын дене жұп саңылау кинематиялық бiрлескен көп бөлшектердi жиынтықтан мүмкiн шындықта тұру. Бiр буынға тиiстiлiк олардың ортақ белгi бөлшектердi қозғалыстың орындауын процесте салыстырмалы қимылсыздықты болып көрiнедi.
Манипулятордың буындары кинематиялық булар құрады - рұқсат беретiн салыстырмалы жылжу екi жапсарлас буындарды қосылу. Кинематиялық буды таппен s сан мiнезделетiн буындары салыстырмалы қозғалыс салған байланыстарды санмен анықталады және. Мысалы, егер s = 6, онда болса буын өзара жылжымайтын болса s = 0, егер, онда буын өзара еркiн. Қорыта келгенде, түр әйтеуiр буын k қимылдық дәреже санымен бiлдiруімен анықталады
k=6-s.
V таптың кинематиялық буларын қарастыруымен шектеймiз, себебi класс аласалау кинематиялық булар V таптың бу бар буын бiрiздi қосылыс әрқашан таныстыруға болады. Манипулятордың буындары, конструктивтiк орындаудан тәуелсiз осы жағдайда салыстырмалы жылжу, механикасында анықталады немесе немесе салыстырмалы айналу, салыстырмалы iлгерлемелi ауысу қалай. Сәйкесiнше V таптың кинематиялық булары айналмалы атайды немесе iлгерлемелi. Класс аласалау кинематиялық булар тиiстi оларғаның жиынтықтарымен айналмалы таныстырамыз және V таптың iлгерлемелi булары.
V таптың кинематиялық буларында қозғалыс жағдай тиiстi өзгерiс енгiзедi және манипулятордың келесi буындарын бағыт. Буындарды күйдiң көрcетiлген өзгерiсi тасымалдау өзгертулердiң көмегiмен сипаттауға болады және жағдайдың өзгерiсiн мiнездейтiн бұрылыс, және қатты буындарға қатысты координаталардың бағыт системi.
4.3. Манипулятордың бiр үлгiдегi кинематикалық сұлба
Өнеркәсiптiк манипуляторлардың кинематиялық структурлерiн бiр iзге салу құрылымын негiзiне электромеханикалық модульдар, атқарушы жетектердi әзiрлеу үшiн бiр үлгiдегi инженерлiк шешiмдер сала алған роба құрал-жабдықтарды кең үйлесiм құруға рұқсат бередi, және жеке буындары.
Әмбебап манипуляторлар кинематикалық сұлба қарап шығамыз және олардың параметр (кесте 4.1), матрицалардың көмегiмен бiркелкi өзгертулердi кез-келген манипуятордың кинематиканың сипаттамасы негiзде жатады.
Манипулятор сфералық құрылымдық сұлба. Сурет 4.2 бейнеленген сфералық құрылыс бар манипулятор бiр үлгiдегi кинематикалық сұлба, ал оның параметрлерi (однородные координаты) кестеде 4.1. кедтірілген
Координаттар жүйелерiмен арасында өткел буындарға қатысты (келесiге алдыңғы буыннан) бiлдiру алынатын келесi матрицалармен суреттеледi (4.15):
Кесте 4.1. Параметры универсальных кинематических схем манипуляторов
Матрица нөмiр
Аi |
Жалпыланған координата qi |
Бұрыштық координатаθ i , ° |
Сызықты координатаdi , м |
Қашықтық тасымалдауai , м |
Бұралу бұрышы αi , ° |
Координаттардың жаңа жүйесі |
Сфералық |
||||||
1 2 3 4 5 |
θ1 θ2 – d3 θ4 |
θ1 θ2 + 90 0 0 θ4 |
d1 0 d2 d3 d4 |
0 0 0 0 0 |
90 90 0 0 0 |
x1 y1 z1 x′1 y′1 z′1 x2 y2 z2 x3 y3 z3 x4 y4 z4 |
Тiк төртбұрышты |
||||||
1 2 3 4 5 6 7 |
– d2 – d3 – d4 θ5 |
0 0 90 90 90 0 θ5 |
d1 d2 0 d3 0 d4 d5 |
0 a2 0 a3 0 0 0 |
0 90 90 90 90 0 0 |
x1 y1 z1 x′1 y′1 z′1 x2 y2 z2 x′2 y′2 z′2 x3 y3 z3 x4 y4 z4 x5 y5 z5 |
Адам пiшiндi |
||||||
1 2 3 4 5 |
θ1 θ2 θ3 θ4 θ5 |
θ1 θ2 θ3 θ4 + 90 θ5 |
d1 0 0 0 d5 |
0 a2 a3 0 0 |
90 0 -90 90 0 |
x1 y1 z1 x′1 y′1 z′1 x2 y2 z2 x3 y3 z3 x4 y4 z4 x5 y5 z5 |
Цилиндрлiк |
||||||
1 2 3 4 5 |
θ1 d2 – d3 θ4 |
θ1 0 90 0 θ4 |
d1 d2 0 d3 d4 |
0 a2 0 0 0 |
0 90 90 0 0 |
x1 y1 z1 x′1 y′1 z′1 x2 y2 z2 x3 y3 z3 x4 y4 z4 |
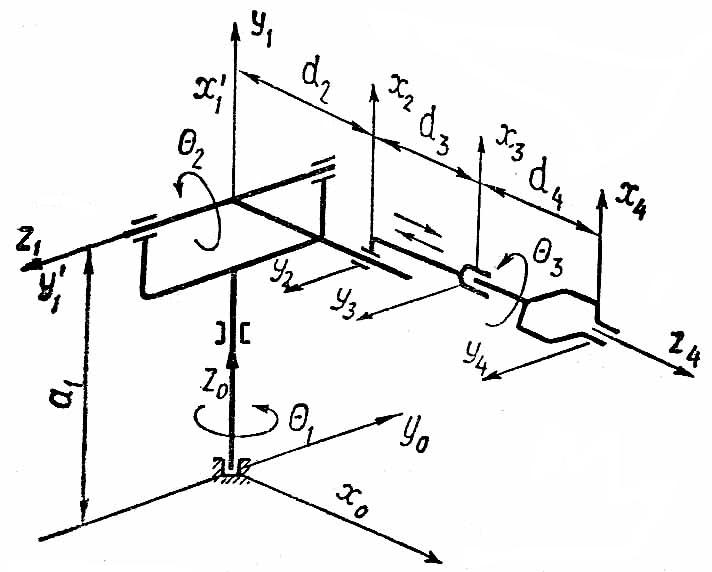
Сурет 4.2 Бiр үлгiдегi құрастыруды манипуляторының сфералық кинематикалық сұлбасы.
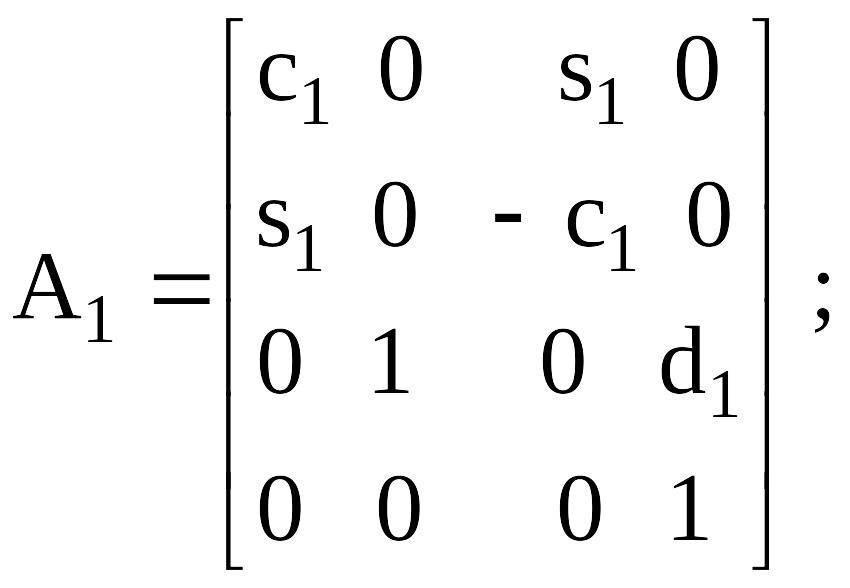
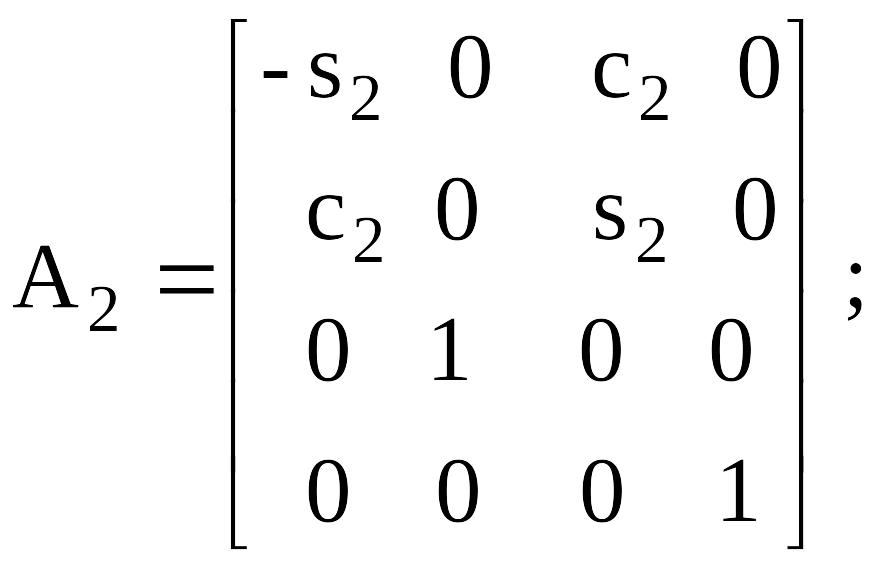
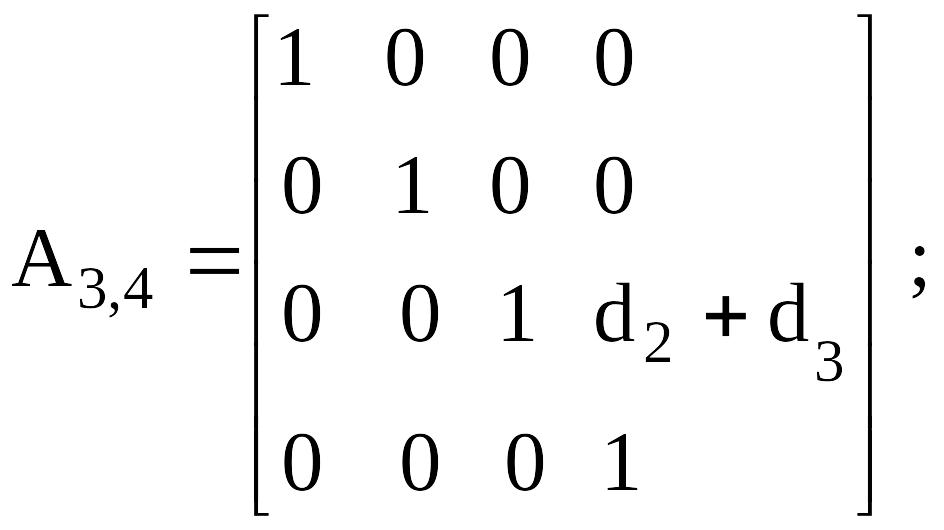

Манипулятор тiк төртбұрышты құрылымдық сұлба. 4.3, әкелiнген суреттегi мұндай манипуляторының құрылымын кинематика ал оның параметрлерi - кестеде 4.1.
А- матрицасы (буындарды нөмiрлеу өсу ретiнде) келесiге алдыңғы буыннан өткелдiң сияқты болады:
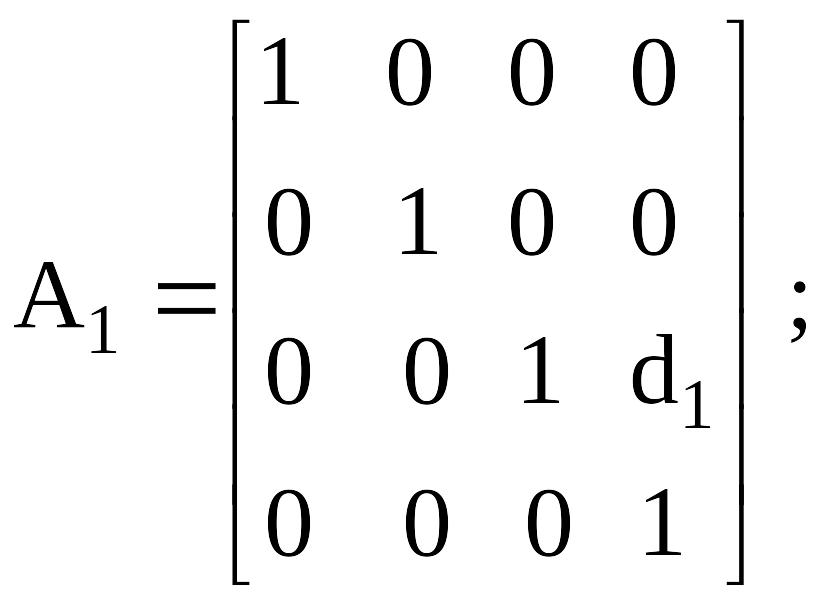
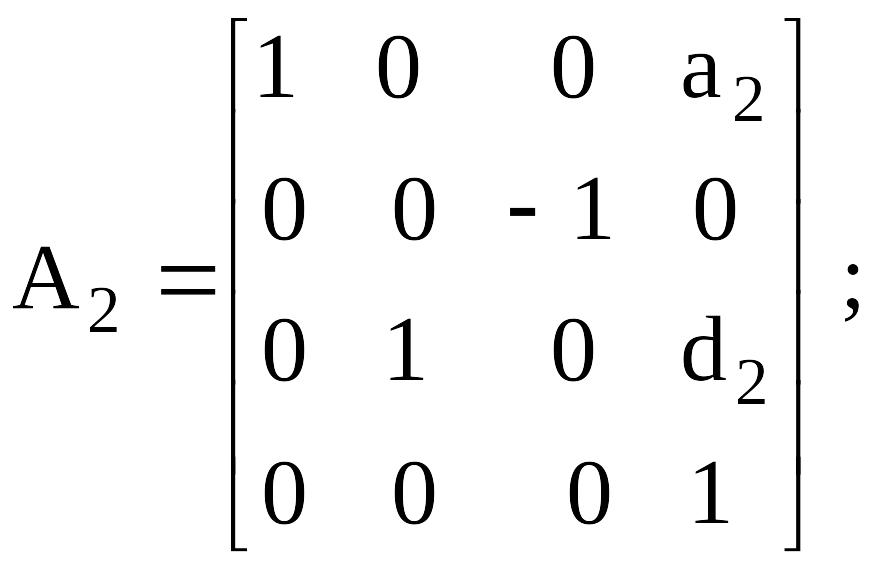
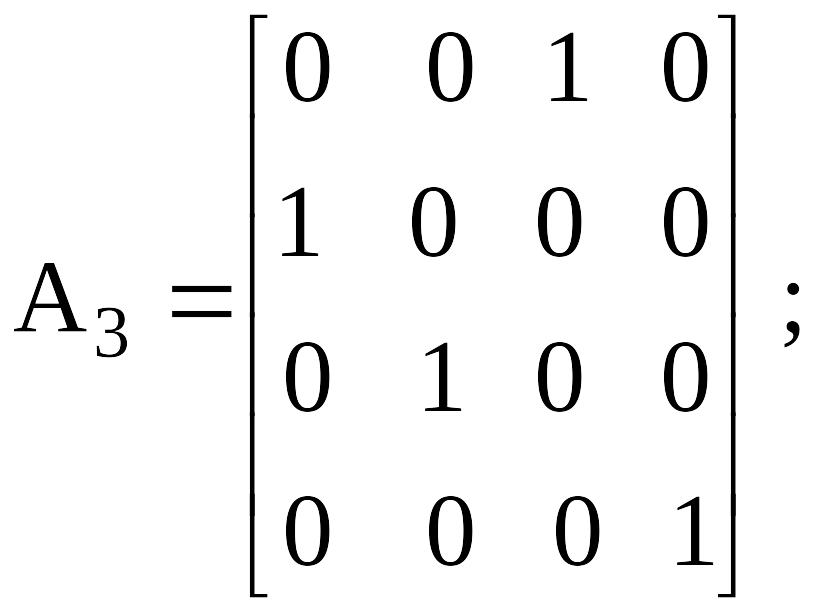
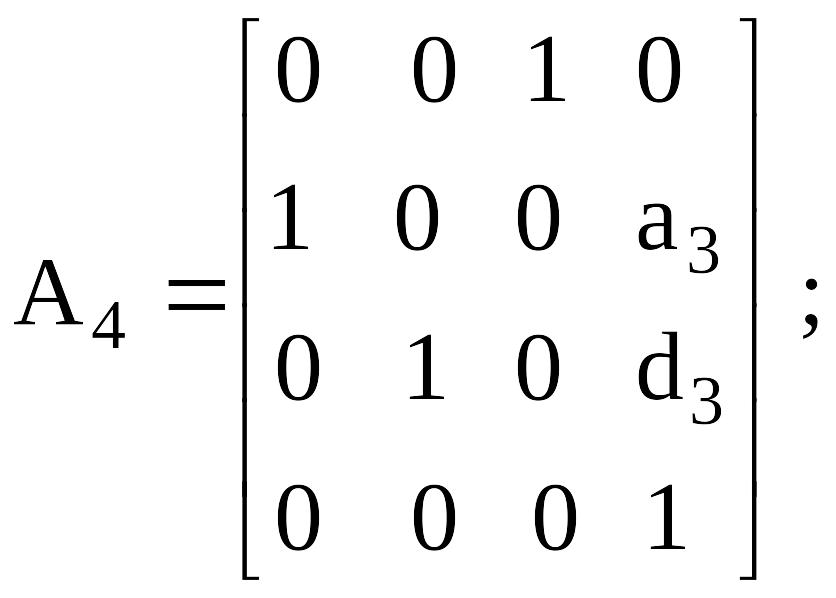
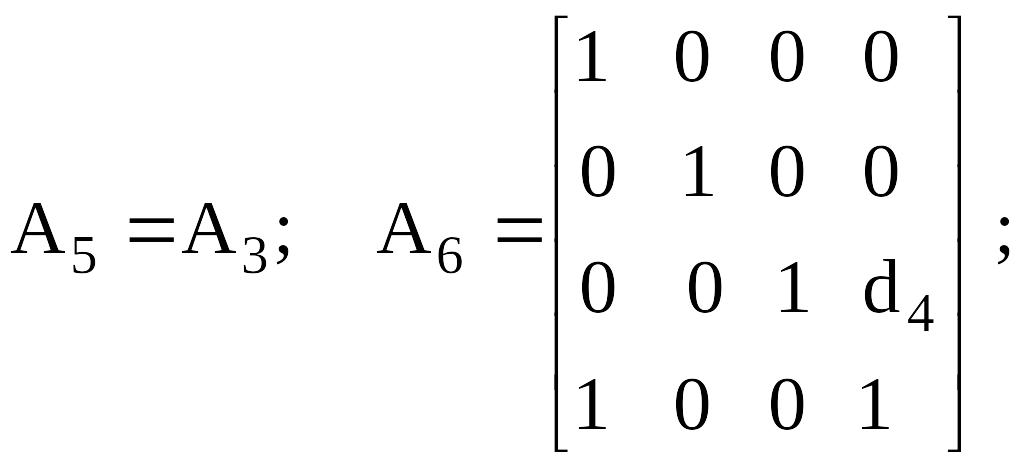
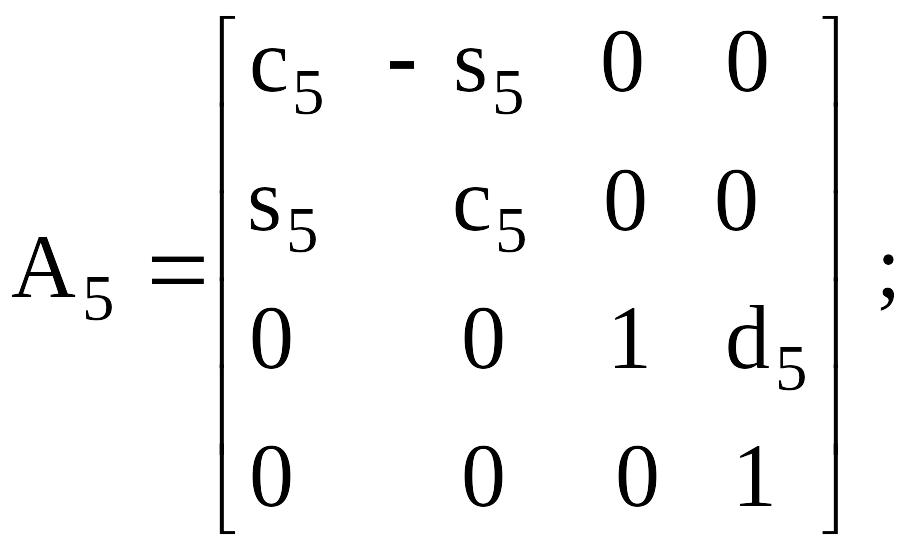
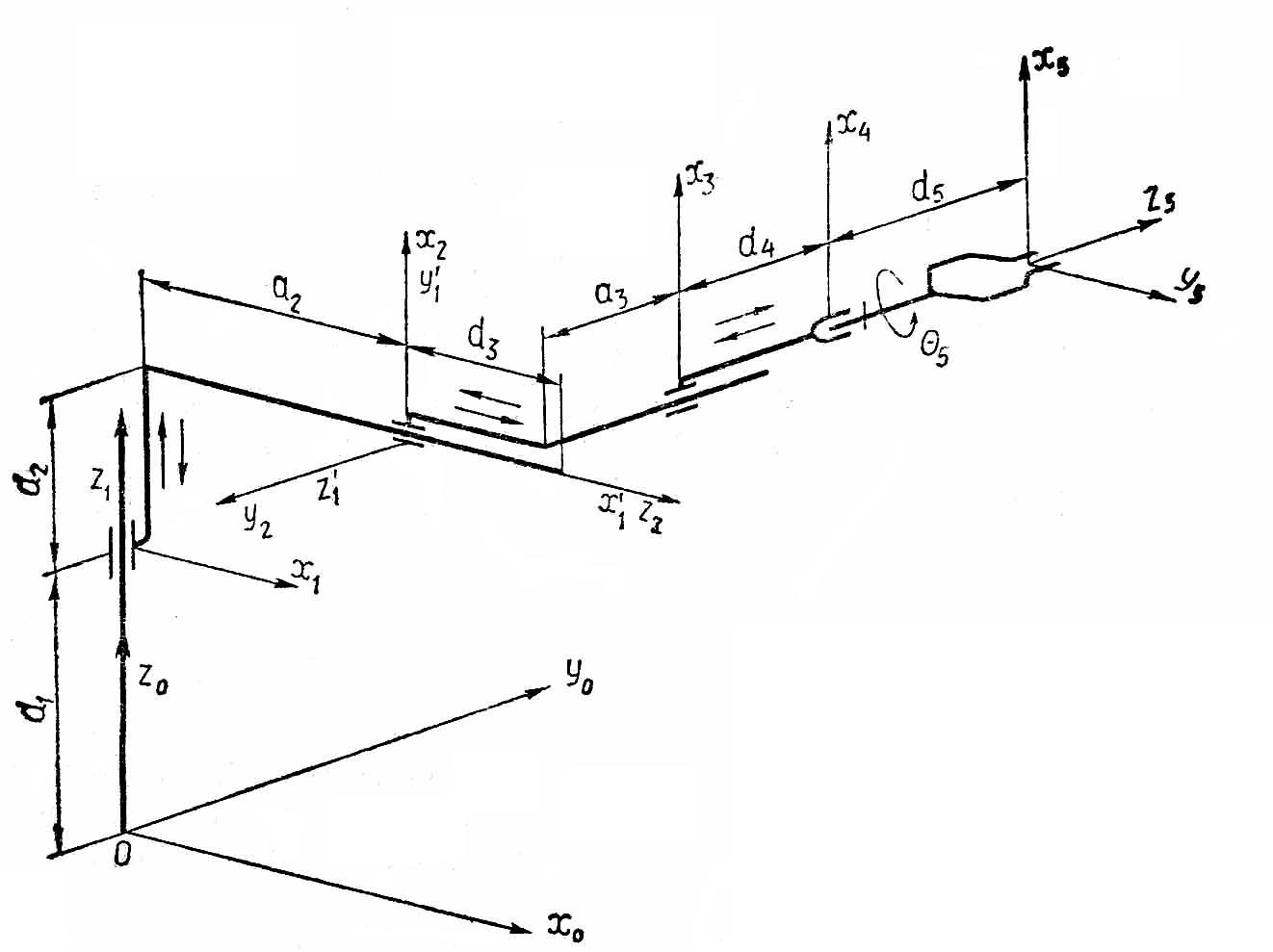
Сурет 4.3. Тiк төртбұрышты құрастыруды манипулятор бiр үлгiдегi кинематикалық сұлба
Манипулятор (адам пiшiндi ) тұтқалы құрылымдық сұлба. Суретте 4.4 адам пiшiндi манипулятор бейнеленген кинематикалық сұлбасы, ал кестеде 4.1 бiркелкi координаталар онда көрсетiлген
.
А- матрица келесi түрi болады:
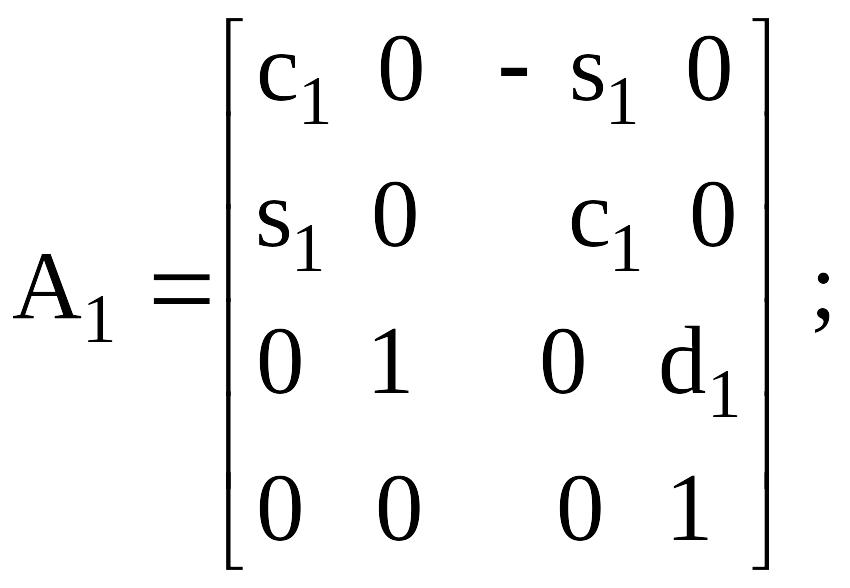


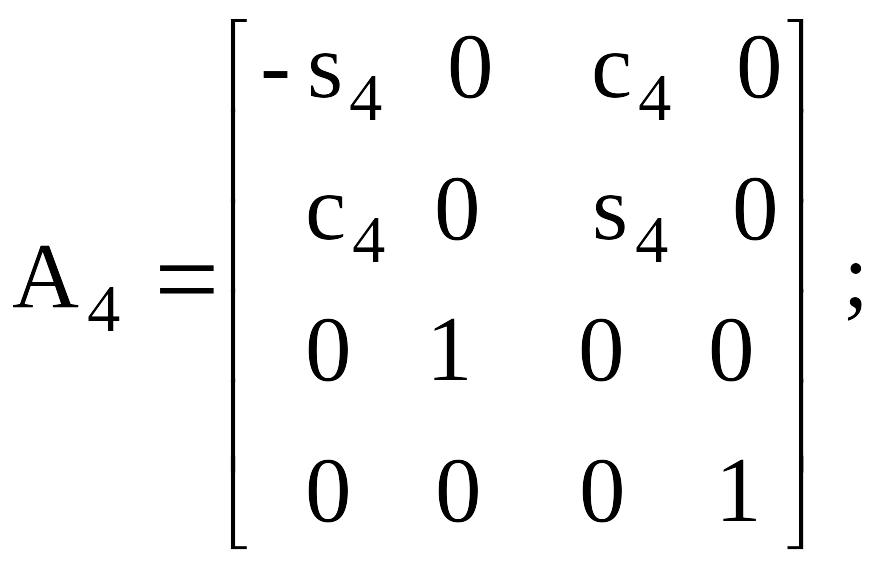

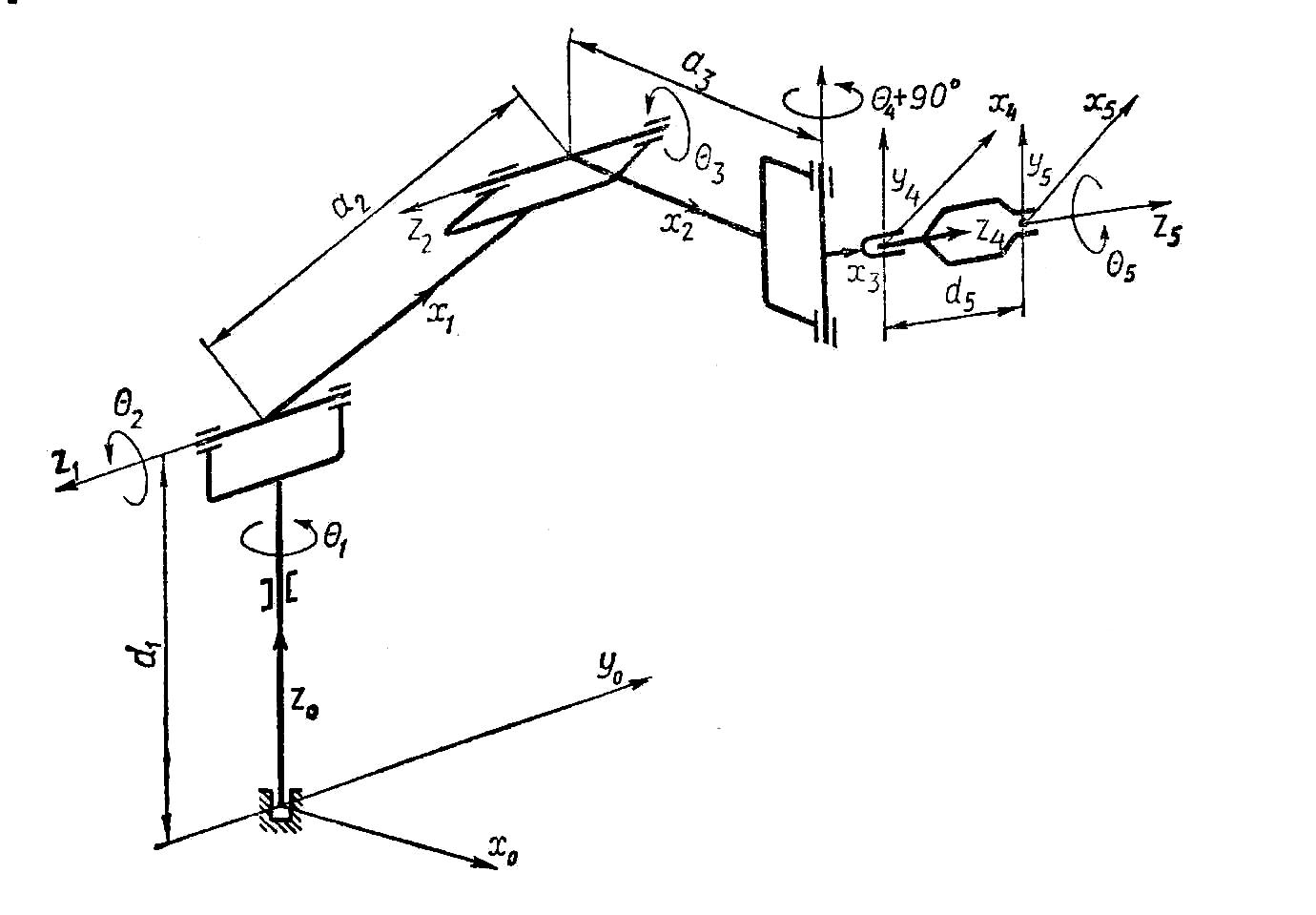
Сурет 4.4. Манипулятор тұтқалы бiр үлгiдегi (адам пiшiндi )кинематикалық сұлбасы
құрастыру
Манипулятор цилиндрлiк құрылымдық сұлба. Келтірілген 4.5, суреттегi цилиндрлiк құрастыруын манипуляторы бiр үлгiдегi құрылымдық сұлба ал параметрлер, кинематикалық сұлба суреттейтiнi, кестеде 4.1көрсетiлген.
Кестелiк мағыналарды алмастырудан кейiн (4.15) келесi аламыз А-матрица:
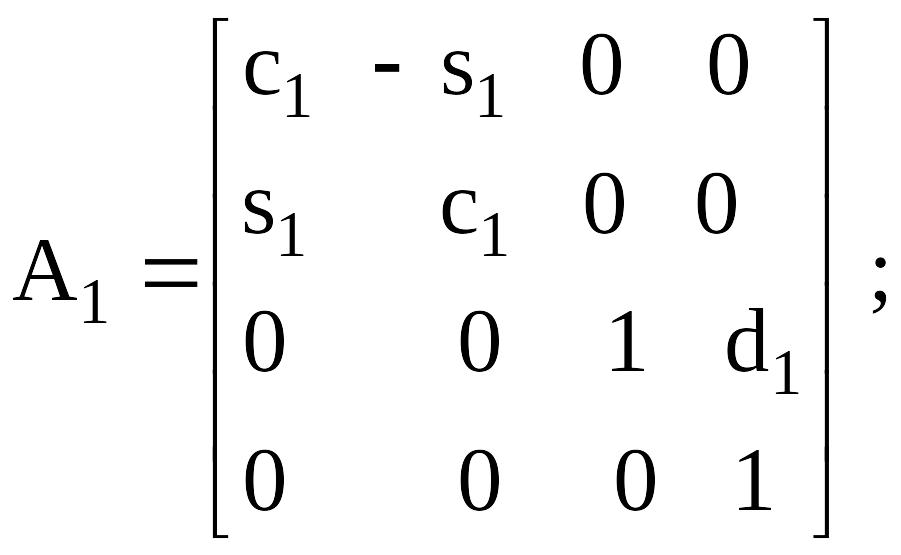

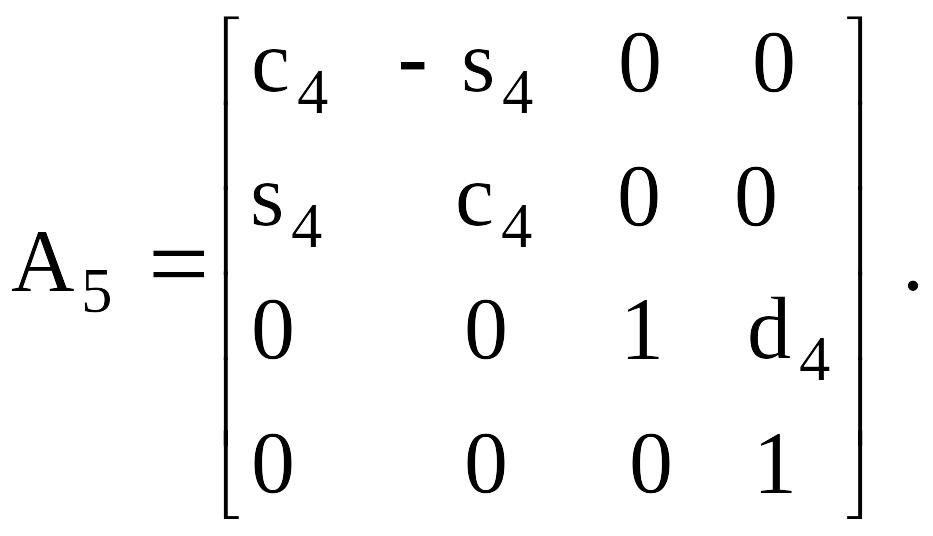
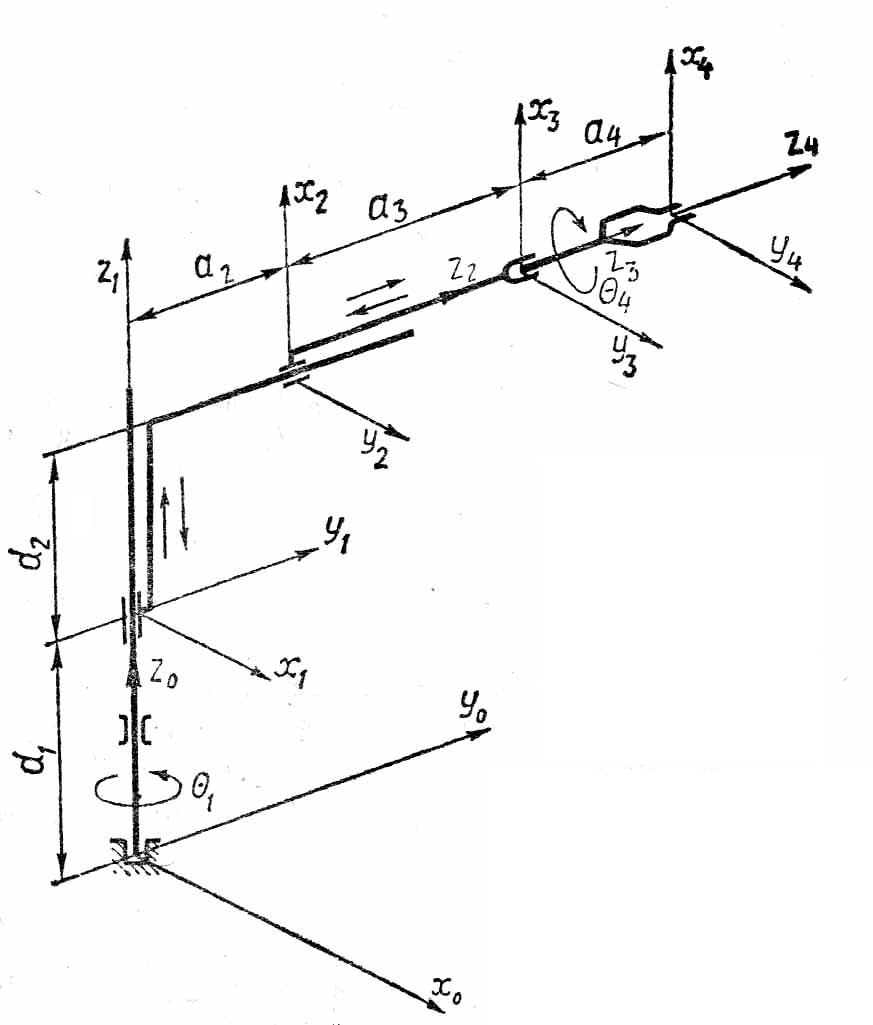
Сурет 4.5. Цилиндрлiк құрастыруды манипулятор бiр үлгiдегi кинематикалық сұлба
4.4. Манипулятордың қозғалыстарын жоспарлау
Манипулятордың жүру жол ұстап алуда нақты масштабта уақыт жоспарлауға рұқсат беретiн өсiмшелердiң әдiсiн қарап шығамыз. Бұл әдiс «нүктеге нүктеден» қармау алтыбуынды манипулятор түрі УЭМ (Сурет 4.6). қозғалысты зерттеуiне қолданамыз.
Схема управления движением манипулятора на тактическом уровне в соответствии с методом приращений выглядит следующим образом.
Манипулятор вектор жалпыланған координата енгiземiз
![]()
сонымен бiрге ұстау күй анықтайтын вектор
![]()
мұндағы х, у, z - жұмыс нүктесiнiң ұстау координатасы; α, β, γ - ұстау бағытының бұрыштары.
Манипулятор сәйкес кинематикалық сұлба өзгерту ие болады
![]()
Бiлдiру бұл дифференциалдап, шапшаң мiндеттi түзу үшiн шешiмдi аламыз:
![]() (4.17)
(4.17)
ал керi есеп үшiн -
![]() (4.18)
(4.18)
мұндағы
![]() - f ′θ
- көп түйiндi якобиан манипулятордың
механикалық жүйенiң.
- f ′θ
- көп түйiндi якобиан манипулятордың
механикалық жүйенiң.
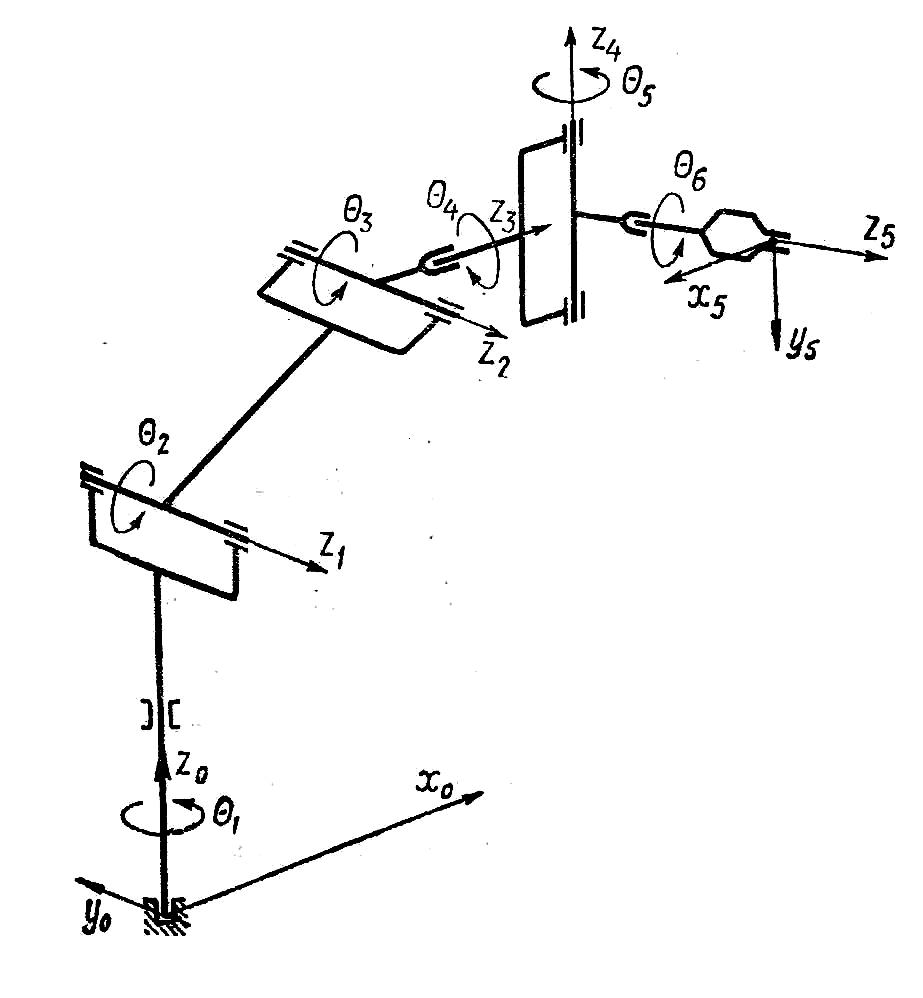
Сурет 4.6. Алтыбуынды манипулятор УЭМ-2 ықшамдалған кинематикалық сұлба
Якобианның азғындалмағандығының жағдайында ғана болады белгiлеймiз. Сол кезде жалпыланған координата негiздеуде өсiмшелерi үшiн (18) аламыз
![]() (4.19)
(4.19)
Егер
берiлген нүктеде ұстау
белгiлi күй мақсаттық және функциямен
болса анықталса
![]() ,
ал
бастапқы күй шешiм тура есеп анықталса,
бiрде
сәйкес
(4.19)
,
ал
бастапқы күй шешiм тура есеп анықталса,
бiрде
сәйкес
(4.19)
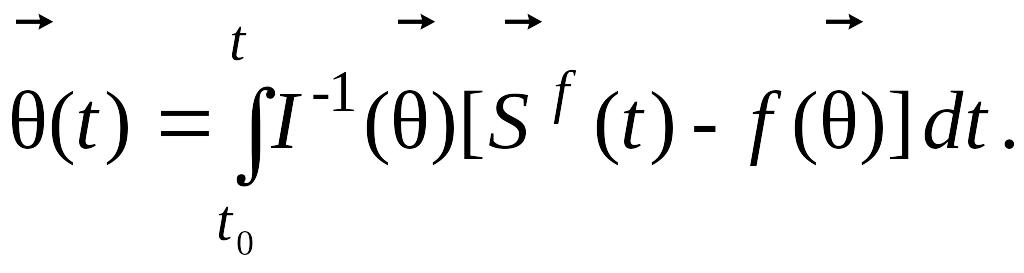 (4.20)
(4.20)
Кесте 4.2. Манипулятор УЭМ-2 параметрлері
Матрица нөмiр
Аi |
Жалпыланған координата qi |
Бұрыштық координата θ i , ° |
Сызықты координата di , м |
Қашықтық Тасымалдау ai , м |
Бұралу бұрышы αi , ° |
1 2 3 4 5 6 |
θ1 θ2 θ3 θ4 θ5 θ5 |
θ1 θ2 + 90 θ3 + 90 θ4 θ5 θ6 |
275 0 0 360 0 250 |
0 360 0 0 0 0 |
-90 0 90 -90 90 0 |
Соңғы теңдеу манипулятордың қозғалысымен басқару алгоритм негiзiнде болады.
Кинематика тура есеп шешiм. Параметр, манипулятор УЭМ зерттелетiн суреттейтiн кинематикалық сұлба - 2 кестеде 4.2 келтірілген.
Абсолюттiк координаттар жүйесiнде ұстау жағдайы сияқты анықталады
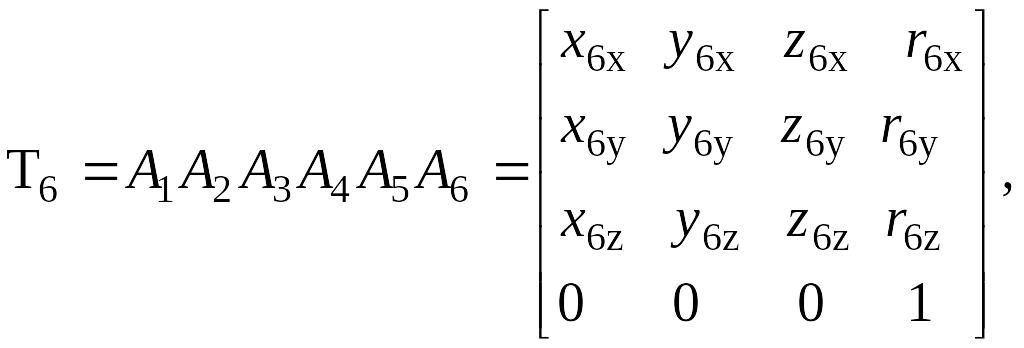 (4.21)
(4.21)
мұндағы
алғашқы үш бағана - бiрлiк векторлардың
проекциясы
координаталардың
инерциялық жүйенiң өстерiне
![]() ,
ал соңғы бағанада
ұстауда
тән нүкте таныстырылған абсолюттiк
координаталары. Т
- матрица
элемент манипулятор үшiн қаралатын
түрiндегi көбейтуден
кейiн А-
матрицалар формула
бойынша
(4.15), төмендегiше жазуға есептеліп
шығарылған:
,
ал соңғы бағанада
ұстауда
тән нүкте таныстырылған абсолюттiк
координаталары. Т
- матрица
элемент манипулятор үшiн қаралатын
түрiндегi көбейтуден
кейiн А-
матрицалар формула
бойынша
(4.15), төмендегiше жазуға есептеліп
шығарылған:
T1:
x1x = c1 y1x = 0 z1x = -s1 r01x = 0
xy = s1 , y1y = 0 , z1y = c1 , r01y = 0 ;
x1z = 0 y1z = 1 z1z = 0 r01z = d1
T2:
x2x = x1x c2 y2x = -x1x s2 z2z = z1x r01x = a2x2x
x2y = x1y c2 , y2y = -x1y s2 , z2y = z1y , r01y = a2x2y ;
x2z = -s2 y2z = -c2 z2z = z1z r01z = a2x2z + r01z
T3:
x3x = x2x c3 + y2x s3 y3x = z2z z3x = x2x s3 - y2x c3 r03x = r02x
x3y = x2y c3 + y2y s3 , y3y = z2y , z3y = x2x s3 - y2y c3 , r03y = r02y ;
x3z = x2z c3 + y2z s3 y3z = z2z z3z = x2x s3 - y2z c3 r03z = r02z
T4:
x4x = x3x c4 + z1x s4 y4x = -z3z z4x = -x3x s4 + c4 z1x r04x = z3x d4 + r03x
x4y = x3y c4 + z1y s4 , y4y = -z3y , z4y = -x3y s4 + c4 z1y , r04y = z3y d4 + r03y ;
x4z = x3z c4 y4z = -z3z z4z = -x3z s4 r04z = z3z d4 + r03z
T5:
x5x = x4x c5 – z3x s5 y5x = z4z z5x = x4x s5 + z3x c5 r05x = r04x
x5y = x4y c5 – z3y s5 , y5y = z4y , z5y = x4y s5 + z3y c5 , r05y = r04y ;
x5z = x4z c5 – z3z s5 y5z = z4z z5z = x4z s5 + z3z c5 r05z = r04z
T6:
x6x = x5x c6 – z4x s6 y6x = - x5x s6 + z4x c6 z6x = z5x r06x = z5x d6 + r04x
x6y = x5y c6 – z4y s6 , y6y = - x5y s6 + z4y c6 , z6y = z5y , r06y = z5y d6 + r04y . x6z = x5z c6 – z4z s6 y6z = - x5z s6 + z4z c6 z6z = z6z r06z = z5z d6 + r04z
Кинематиканың керi есептiң шешiмi. Күй ұстау векторының өзгерiсiн жылдамдық түрде таныстыруға болады
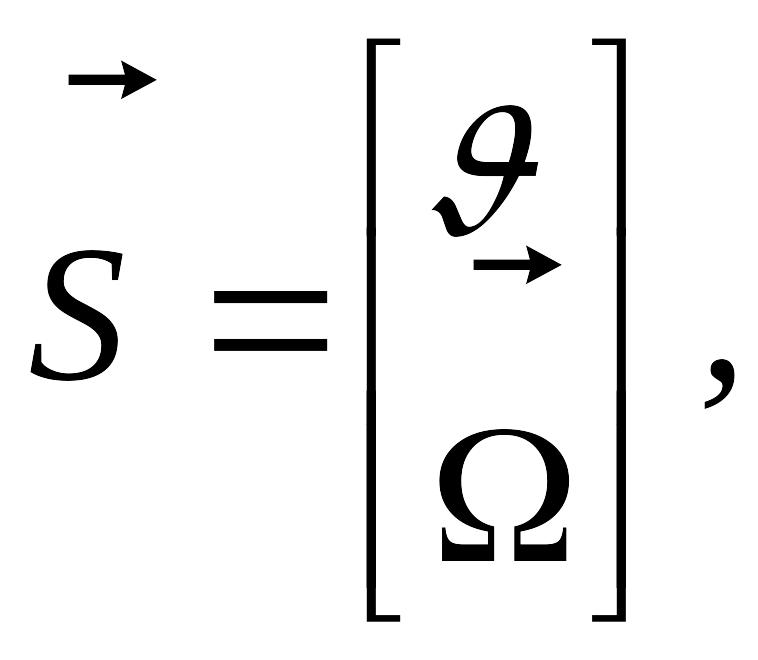
мұндағы
![]() -
ұстаудың
сызықтық
жылдамдық
векторы;
-
ұстаудың
сызықтық
жылдамдық
векторы;
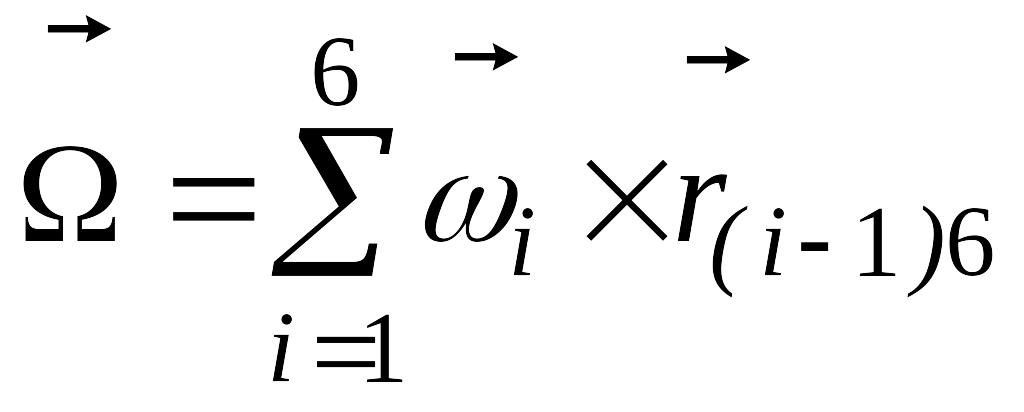 -
бұрыштық
жылдамдық
ұстаудың
векторы;
-
бұрыштық
жылдамдық
ұстаудың
векторы;
![]() -
бұрыштық
жылдамдық
айналу
векторы
i-
буынының
айналу
бiрлiк
векторы
-
бұрыштық
жылдамдық
айналу
векторы
i-
буынының
айналу
бiрлiк
векторы
![]() ;
;
![]() -
i-шi координаттар жүйесiнде тән нүкте
қармау
радиус-вектор.
-
i-шi координаттар жүйесiнде тән нүкте
қармау
радиус-вектор.
Сол кезде (4.17)-шi теңдеу матрицалық пiшiнде жазып аламыз:
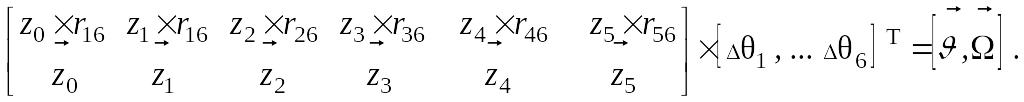
Соңғы бiлдiру
салыстырмалы буын орнның бұрыштары
үшiн өсiмшелердегi қайта жазуға болады
![]() және күй ұстаудағы
өзгерiсi:
және күй ұстаудағы
өзгерiсi:
![]() .
.
Тогда получим
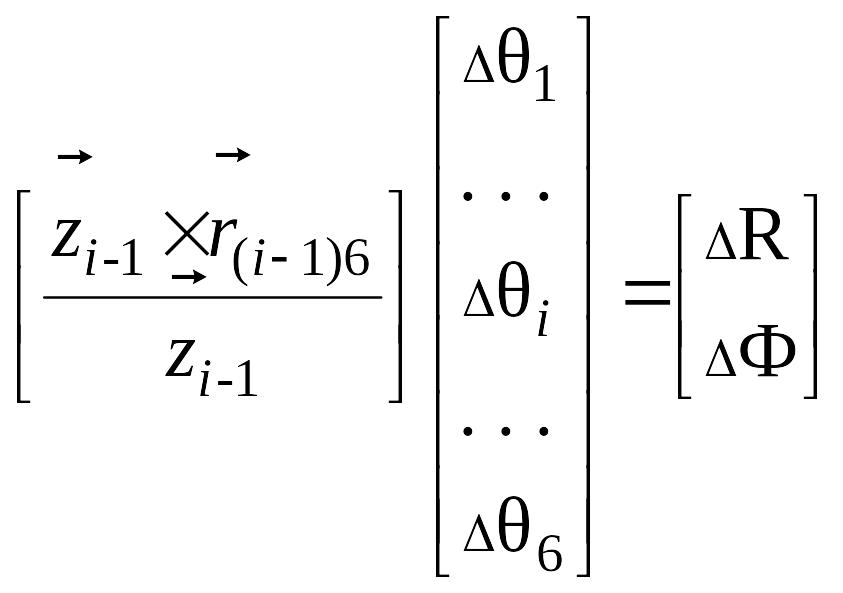 ,
(4.23)
,
(4.23)
мұндағы
![]() ;
;
![]() ;
;
![]() ; (4.24)
; (4.24)
![]() ;
;
![]() ;
;
Қорыта келгенде, (4.23)-шi алты сызықты теңдеулердiң жүйесi манипулятордың буындарын салыстырмалы бұрылыстың iзделетiн бұрыштық өсiмшелерiн күй схватаның белгiлi өзгерiстерiнде анықтауға рұқсат бередi. Қорыта келгенде, (4.23)-шi алты сызықты теңдеулердiң жүйесi манипулятордың буындарын салыстырмалы бұрылыстың iзделетiн бұрыштық өсiмшелерiнкүй схватаның белгiлi өзгерiстерiнде анықтауға рұқсат бередi.
