1.Линейные электрические цепи синусоидального тока
1.1.Установившийся режим линейной электрической цепи, питаемой от источников синусоидальных эдс и токов
Электрической
цепью переменного тока принято называть
совокупность устройств и объектов,
образующих путь для электрического
тока, электромагнитные процессы в
которых могут быть описаны с помощью
понятий ЭДС, тока и напряжения, последние
являются функциями
времени:
;
;
- созданы переменным во времени
электрическим полем, его векторы
и
.
Для ЭДС е,
тока i
и напряжения u
заданы их мгновенные значения, т.е.
значения в дискретный момент времени.
Вектор плотности тока состоит из двух
составляющих
- плотности тока проводимости и плотности
тока смещения (последняя составляющая
в цепях постоянного тока отсутствует).
Дальнейшее рассмотрение проведем на примере синусоидального тока. Его аналитическое выражение
.
(3.1)
График синусоидальной функции времени для этого тока приведен на рис. 3.1.
Гармоническое
колебание i(t)
характеризуется следующими основными
параметрами: амплитудой
,
угловой (круговой)
частотой w,
начальной фазой
.
Наименьший промежуток времени, по истечении которого значения функции i(t) повторяются, называется периодом Т. Между периодом Т и круговой частотой w существует простая связь:
. (3.2)
Величину, обратную
периоду, называют
циклической частотой:
.
Из выше изложенного следует, что
.
Единицей измерения частоты f
является Герц (Гц), угловой частоты w
- радиан в секунду (
).
Для питания различных электроэнергетических
установок в России принята промышленная
частота f=50
Гц, значит угловая частота
.
В (3.1) выражение в
скобках
- фаза синусоидального электрического
тока (фаза тока) - аргумент синусоидального
тока, отсчитываемый от точки перехода
тока через нуль к положительному
значению. В этой формулировке заключен
смысл начала отсчета времени. При
- начальная фаза синусоидального
электрического тока - значение фазы
синусоидального тока в начальный момент
времени.
На оси времени t
удобнее откладывать время в специальных
единицах
.
Аналогичный вид имеют выражения для синусоидального напряжения u, ЭДС е, тока источника J:
.
(3.3)
Важными параметрами гармонических колебаний являются их действующие и средние значения. Действующее значение тока i равно среднеквадратичному за период значению:
. (3.4)
Аналогично вводят действующие значения напряжения и ЭДС:
. (3.5)
Важно знать, что в паспорте электротехнических устройств синусоидального тока указаны действующие значения напряжений U и токов I; большинство измерительных приборов проградуированы так, что они показывают действующие значения синусоидальных токов и напряжений.
Среднее
значение
тока i
определяется за пол периода
:
. (3.6)
Аналогично определяем, что
.
(3.7)
Отношение
действующего значения к среднему
значению называется коэффициентом
формы кривой
для синусоиды:
.
При включении идеального источника синусоидальной ЭДС е на нагрузку в виде линейного пассивного двухполюсника ЛПД, схема которого содержит линейные элементы R, L, C в различной комбинации, в цепи протекает синусоидальный ток i (рис. 3.2, а).
Напряжение на зажимах двухполюсника u=e так же синусоидально.
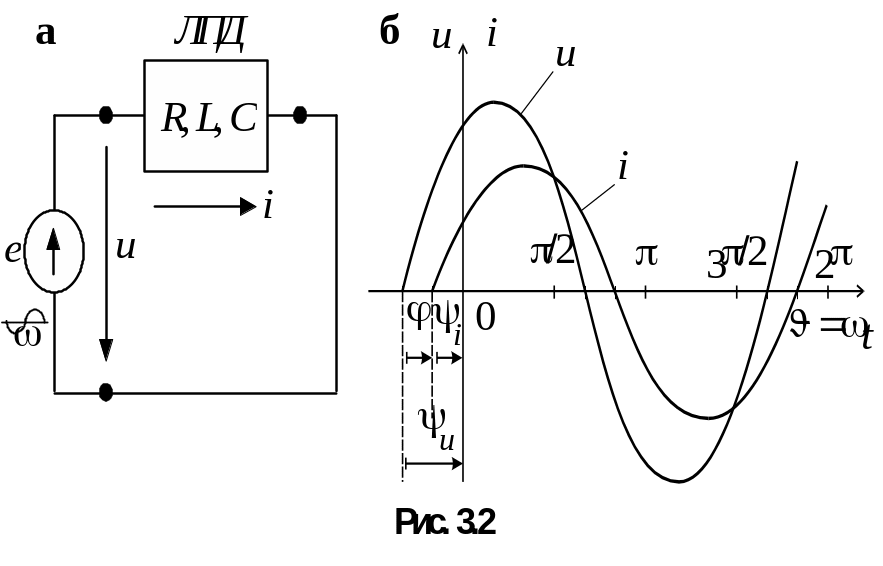
графически изображены на рис. 3.2, б. Синусоиды сдвинуты друг относительно друга на фазовый угол j.
Угол сдвига фаз между напряжением и током j - алгебраическая величина, определяемая путем вычитания начальной фазы тока из начальной фазы напряжения:
. (3.8)
Возможные значения угла по знаку:
j>0 - напряжение опережает ток;
j<0 - напряжение отстает от тока;
j=0 - напряжение и ток совпадают по фазе.
Определим начальную
фазу
через начальную фазу напряжения
и фазовый угол сдвига j:
.
Тогда выражение для тока примет вид:
. (3.9)
Анализируя выражения (3.8) и (3.9) в зависимости от значения угла j, говорят, что при j=0 напряжение и ток совпадают по фазе; при j = ±p они противоположны по фазе и при j=±p/2 - находятся в квадратуре.