Электроемкость

Если проводнику сообщить некоторый заряд, то на нем установится некоторый потенциал. Причем, если проводник уединенный, то есть находится вдали от других зарядов, то потенциал проводника прямо пропорционален величине его заряда. Пусть заряд уединенного проводника равен q а его потенциал равен φ. Величина

называется электроемкостью или просто емкостью проводника. Единицей измерения емкости в системе СИ является Фарада [Ф].

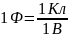
Емкость проводника является характеристикой проводника. Она определяется формой и геометрическими размерами проводника, а также диэлектрическими характеристиками среды.

Потенциал проводящего шара радиусом r, имеющего заряд q, равен

Значит, емкость проводящего шара равна .

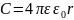Одна фарада – это очень большая емкость. Для того чтобы емкость шара была равна 1 Ф, его радиус должен быть равен 9·10⁹ м – это примерно в 1500 раз больше радиуса Земли.

Энергия электрического поля уединенного проводника может быть выражена через его емкость:

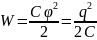
Конденсаторы

Уединенные проводники имеют очень маленькую емкость. Следовательно, они не могут нести на себе значительные заряды. Однако имеется необходимость в устройствах, которые могут накапливать большие заряды и, соответственно, иметь большую энергию электрического поля. Такие устройства называются конденсаторами. Конденсаторы делают в виде двух проводников, расположенных близко друг к другу. Простейший и самый распространенный конденсатор представляет собой две параллельные проводящие пластины, расположенные друг от друга на расстоянии значительно меньшим, чем размеры пластин. Пластины заряжают одинаковым по модулю и противоположным по знаку зарядом. При этом все силовые линии, выходящие из положительно заряженной пластины, заканчиваются на отрицательно заряженной пластине. Снаружи электрического поля практически нет и внешние поля не оказывают на конденсатор никакого влияния.

О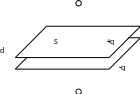 сновной характеристикой конденсатора является емкость. Емкостью конденсатора называется отношение модуля заряда на его пластинах к разности потенциалов между ними:

Разность потенциалов очень часто называют напряжением и обозначают U.

Мы, в основном, будем использовать модельное понятие – идеальный конденсатор. Идеальным называется конденсатор, расстояние между пластинами которого пренебрежимо мало по сравнению с размерами пластин. Электрическое поле идеального конденсатора однородное и полностью сосредоточено между пластинами. Снаружи электрическое поле идеального конденсатора везде равно нулю.

Пусть имеется плоский конденсатор, состоящий из двух пластин площадью S каждая, находящихся на расстоянии d малом по сравнению с размерами пластин. Если пластины зарядить равными по модулю и противоположными по знаку зарядами q, то напряженность поля между пластинами будет равна

Для увеличения емкости конденсатора между его пластинами обычно помещают диэлектрик. Если диэлектрическая проницаемость диэлектрика равна ε, то напряженность поля между пластинами конденсатора равна:

Так как электрическое поле между пластинами однородно, то разность потенциалов (напряжение) равна:

Значит, емкость плоского конденсатора равна:

Энергия электрического поля конденсатора складывается из энергий электрического поля его пластин. Пусть потенциал положительно заряженной пластины равен φ₁, а отрицательной – φ₂. Если модуль заряда пластин равен q то

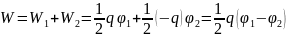
Учитывая определение емкости можно написать следующие формулы для энергии электрического поля конденсатора:

Подставив в эту формулу выражение для емкости конденсатора, получаем:

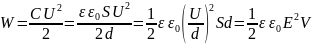
Здесь 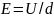- напряженность поля между пластинами, а 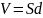- объем между пластинами. Так как электрическое поле конденсатора полностью сосредоточено между пластинами, то энергия, приходящаяся на единицу объема, равна

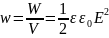
Эта величина называется плотностью энергии электрического поля. Эта формула была получена нами для однородного электрического поля конденсатора. Однако, она справедлива для произвольного электрического поля.

Соединение конденсаторов

Р ассмотрим некоторые положения, касающиеся соединения конденсаторов. В первую очередь следует иметь в виду, что схемы, содержащие конденсаторы, собирают из незаряженных конденсаторов (если специально не оговорено). Поэтому изначально заряды на всех конденсаторах в цепи были равны нулю. Только после подключения цепи к источнику напряжения конденсаторы заряжаются.

Пусть имеется некоторая цепь, содержащая конденсаторы. Рассмотрим некоторый узел цепи, в котором сходятся несколько конденсаторов. Рассмотрим систему, состоящую из пластин, сходящихся в узел. На рисунке эта система выделена пунктирным контуром. Так как изначально конденсаторы были не заряжены, то заряд всех пластин был равен нулю. Значит суммарный начальный заряд рассматриваемой системы был равен нулю. Но выделенная система пластин является электрически изолированной (заряд не может переходить с одной пластины конденсатора на другую). Значит, после зарядки конденсаторов суммарный заряд этой системы должен также быть равен нулю. Отсюда получаем правило: алгебраическая сумма зарядов пластин всех конденсаторов, сходящихся в один узел, равна нулю.

Теперь рассмотрим простейшие схемы соединения конденсаторов: последовательное и параллельное соединение.

1 ) Последовательное соединение.

Пусть конденсаторы емкостью С₁, С₂, С₃,… соединены последовательно. Любая точка между соседними конденсаторами (например, точка О) может рассматриваться как узел, в который сходятся два конденсатора (С₁ и С₂). Это означает, что суммарный заряд соединенных друг с другом пластин соседних конденсаторов должен быть равен нулю, то есть эти пластины должны быть заряжены одинаковым по модулю и противоположным по знаку зарядом. Получается, что при последовательном соединении заряды на всех конденсаторах одинаковые:

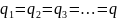
Напряжение на каждом конденсаторе численно равно работе, совершаемой силами электрического поля при переносе единичного положительного заряда с положительно заряженной пластины на отрицательно заряженную. А общее напряжение численно равно работе, совершаемой силами поля при переносе единичного положительного заряда с положительной клеммы схемы на отрицательную клемму. Но эта общая работа будет равна сумме работ, совершаемых при последовательном переходе через каждый конденсатор. Значит, при последовательном соединении конденсаторов общее напряжение равно сумме напряжений на всех конденсаторах:

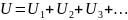
Определим общую емкость. Общей емкостью схемы конденсаторов называется емкость конденсатора, который при напряжении, равном суммарному напряжению на схеме, будет иметь заряд, равный суммарному заряду схемы. Так как при последовательном соединении заряды всех конденсаторов одинаковы и равны, например, q, то и суммарный заряд схемы тоже равен q. Обозначим суммарную емкость С. Тогда общее напряжение равно

Так как это напряжение складывается из напряжений на каждом конденсаторе, то можно написать:

Сокращая на q, получаем формулу для общей емкости при последовательном соединении конденсаторов:

2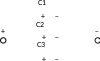 ) Параллельное соединение.

Пусть конденсаторы емкостью С₁, С₂, С₃,… соединены параллельно. Так как все левые пластины конденсаторов подключены к одной и той же положительной клемме, то потенциалы всех левых пластин одинаковы и равны потенциалу положительной клеммы. По тем же соображениям, потенциалы всех правых пластин конденсаторов одинаковы и равны потенциалу отрицательной клеммы. Поэтому при параллельном соединении напряжения на всех конденсаторах одинаковые и равны общему напряжению:

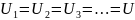
К положительной клемме схемы сходятся все положительно заряженные пластины конденсаторов, а к отрицательной – все отрицательно заряженные пластины. Значит, при параллельном соединении суммарный заряд схемы равен сумме зарядов на всех конденсаторах:

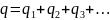
Если общую емкость схемы обозначить С, то можно написать:

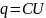
С учетом предыдущего соотношения:

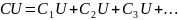
Сократив на U, получаем формулу для общей емкости при параллельном соединении конденсаторов: