2.4. Экономизация степенных рядов при помощи полиномов чебышева

Полиномы Чебышева определяются следующим образом:

где .

Иными словами,

(2.1)

Для вычисления полиномов Чебышева обычно используют рекуррентное соотношение, устанавливающее связь между T_n–1(x), T_n(x) и T_n+1(x):

Свойства полиномов Чебышева (рис.2.2):

Рис 2.2 Графики полиномов Чебышева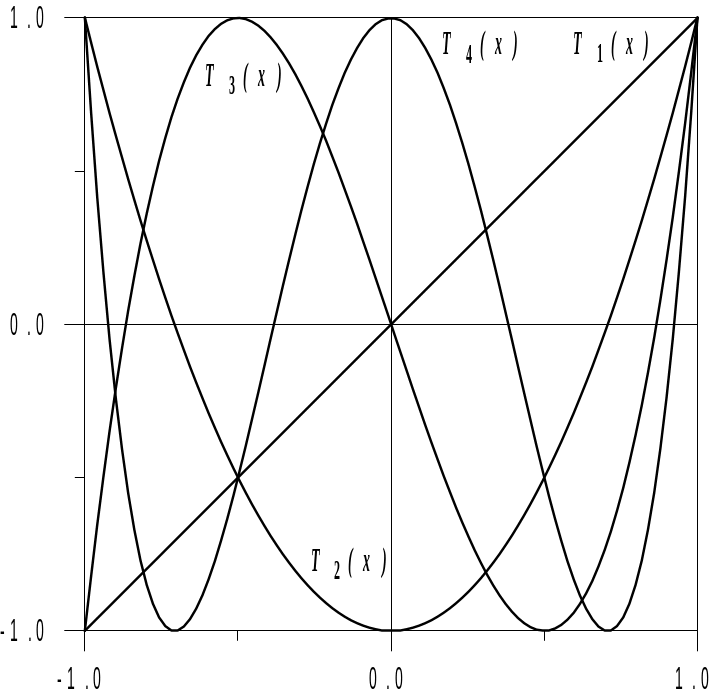

1) область определения – отрезок x [–1, 1];

2) коэффициент при старшей степени в T_n (x) равен 2^n–1 ;

3) нули (корни) полиномов Чебышева определяются формулой

; (2.2)

они расположены неравномерно и сгущаются к концам отрезка;

4) координаты экстремумов

,

причем все максимумы равны 1, а минимумы равны –1;

5) из всех возможных полиномов степени n со старшим коэффициентом, равным 1, точная верхняя грань абсолютных значений на отрезке [–1, 1] наименьшая у полинома T_n(x)/2^n–1.

Это основное свойство полиномов Чебышева, поэтому их называют полиномами, наименее отклоняющимися от нуля¹.

Действительно, рассмотрим полином (n–1)-ой степени

,

где P_n(x) – произвольный полином n-ой степени со старшим коэффициентом, равным 1. Допустим, что отклонение P_n(x) от нуля на [–1, 1] меньше, чем у T_n(x)/2^n–1 . Это означает, что

,

где x_k – координаты экстремумов полинома T_n(x):

T_n(x_k)=(–1)^k, k=0, 1,..., n.

Следовательно, полином _n–1(x) попеременно будет принимать положительные и отрицательные значения в (n+1)-ой точке, то есть он должен иметь по крайней мере n корней, что невозможно (это полином n–1-ой степени), кроме тривиального случая

.

На этом свойстве основывается экономизация степенных рядов.

Пусть дан отрезок степенного ряда функции

на отрезке [–1, 1] . Как уже отмечалось, ошибка для степенного ряда обычно велика на концах отрезка и мала в середине.

Выразим степени х через полиномы Чебышева:

и превратим отрезок степенного ряда в отрезок ряда по полиномам Чебышева:

Для широкого класса функций разложение по {T_n(x)} сходится много быстрее, чем по любой другой системе полиномов, так как b_k убывают быстрее, чем a_k.

Пример. Экономизировать отрезок степенного ряда

Подставляя вышеприведенные зависимости и приводя подобные члены, получаем

Отбросим в первом выражении последний член х⁵/5. Тогда погрешность приближения ₁  1/5 = 0,2. Отбросим во втором выражении три последних члена. Тогда погрешность ₂  7/48 + 1/32 + 1/80  0,145+0,032+0,0125  0,189<0,2.

Таким образом, данную функцию можно представить полиномом 2-ой степени более точно

,

чем отрезком из 5 членов степенного ряда.

Чебышевское разложение снова можно превратить в многочлен по степеням x:

Ряд экономизирован.

Примечание. Ограничение области изменения переменной х отрезком [–1,1] не уменьшает общности. Степенной ряд относительно переменной x, заданной на отрезке a  x  b, легко превращается в ряд по переменной t[–1, 1] заменой

(2.3)

Конец примечания.

2.5 Дробно–рациональные приближения

Некоторые функции нельзя с достаточной точностью приблизить полиномами. Кроме того, полиномиальное приближение может очень медленно сходиться. В таких случаях используется дробно-рациональное приближение функции – в виде отношения двух многочленов.

Рассмотрим снова разложение функции в ряд Тейлора:

Представим эту функцию в виде отношения двух полиномов:

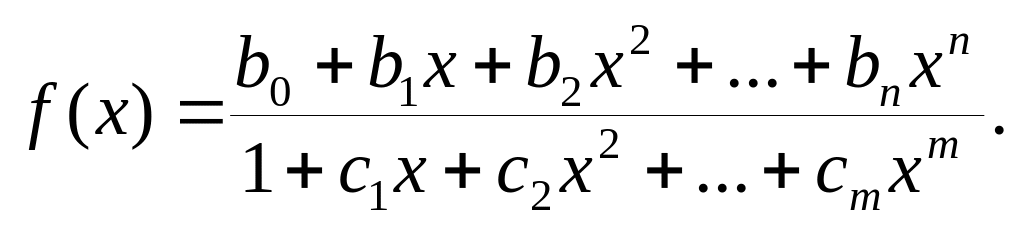
Равенство единице первого члена полинома в знаменателе не нарушает общности выражения, т.к. любое другое число можно превратить в 1, поделив на него числитель и знаменатель.

Возникает задача – определить коэффициенты b_k и с_k, считая известными коэффициенты a_k. Для этого необходимо n+1+m уравнений и столько же членов ряда Тейлора:

Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях х, получаем:

и так далее.

Решая эту систему линейных алгебраических уравнений, получаем b_k и с_k .

Пример.

Решая систему, находим:

Следовательно,

то есть это приближение по точности равносильно аппроксимации рядом Тейлора с учетом членов до 4–ого порядка включительно.

Отметим, что для расчета по ряду Тейлора (с использованием схемы Горнера) необходимо 2n=8 действий (4 умножения и 4 сложения), а для дробно–рационального приближения – 6 действий (3 умножения и деления и 3 сложения и вычитания).

Кстати, можно еще сократить количество вычислений, представив дробно–рациональное выражение в виде цепной дроби:

Здесь процесс вычисления осуществляется за 5 действий.