- •Механика - математика факультеті Дифференциалдық теңдеулер және басқару теориясы кафедрасы
- •Пәннің оқу-әдістемелік кешені Математика
- •Алматы 2013ж. Поәк дайындаған Елдесбай т. Ф.-м.Ғ.Д, профессор
- •Факультеттің әдістемелік (бюро) кеңесінде ұсынылды.
- •1. Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі
- •2. Түзудің жалпы теңдеуі
- •6. Берілген нүктеден өтетін түзудің теңдеуі
- •1. Берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі
- •2. Жазықтықтың жалпы теңдеуі
- •4. Жазықтықтың кесінділік теңдеуі
- •6. Нүктеден түзуге дейінгі қашықтық
- •2. Түзудің канондық теңдеуі
- •2. Эллипс
- •3. Гипербола
- •4. Парабола
- •5. Екінші ретті қисықтың жалпы теңдеуі
- •3. Kонус
- •7. Екі қуысты гиперболоид:
- •2. Аралықта өсетін және кемитін функциялар
- •3. Жұп және тақ функциялар.
- •Бірінші тамаша шек. Құрамында тригонометриялық функциялар бар өрнектердің шектерін есептегенде бірінші тамаша шекті қолданады: . Дәлелдеу: Радиусы бірге тең шеңбер аламыз. , сонда:
- •Екінші тамаша шек: .
- •Kесіндіде үзіліссіз функциялардың қасиеттері
- •Параметр арқылы берілген функцияның туындысы. Функциясын кейде параметрлік түрде жазған ыңғайлы болады
- •Дифференциалды есептеу формулаларын келтірейік:
- •Анықталған интегралдың анықтамасы. Функциясы кесіндісінде анықталсын, мұнда . Төменгі амалдарды орындаймыз.
- •3−Мысал.
- •3. Қисық доғасының ұзындығы
- •2. Ақырсыз функцияның меншіксіз интегралы
- •2.3 Тәжірибелік (семинар) сабақтарының жоспары.
- •2.4 Оқытушының жетекшілігімен орындалатын студенттердің өзіндік жұмыстары бойынша өткізілетін сабақтардың жоспары (соөж)
- •2.5. Студенттердің өздік жұмыстары бойынша сабақ жоспары (сөж)
- •2.6. Курс бойынша жазбаша жұмыстың тақырыптары
- •2.7. Өздік бақылау үшін тест тапсырмалары
- •2.8. Курс бойынша емтихандық сұрақтар
Kесіндіде үзіліссіз функциялардың қасиеттері
1. Егер функциясы кесіндісінде үзіліссіз болса, онда ол осы кесіндіде ақырлы (шенелген)
2. Вейерштрасс теоремасы Егер функциясы кесіндісінде үзіліссіз болса, онда ол осы кесіндіде өзінің ең кіші және ең үлкен мәндерін қабылдайды.
3.
Больцано-Коши теоремасы
Егер
функциясы
кесіндісінде үзіліссіз және және
,
нүктелеріндегі мәндері әртүрлі таңбалар
қабылдаса (![]() ),
онда
),
онда
![]() теңдігі орындалатындай
кесіндісінің ең болмағанда
теңдігі орындалатындай
кесіндісінің ең болмағанда
![]() бір нүктесі бар.
бір нүктесі бар.
Әдебиеттер: 1 нег.[159-162], [164-169], [191-211], 11 қос. [335-358].
Бақылау сұрақтар:
1. Бірінші тамаша шек.
2. е санының анықтамасын келтіріңіз (екінші тамаша шек).
3. Функцияның нүктедегі үзіліссіздігінің анықтамасын беріңіз.
4. Қандай нүктелер функцияның үзіліс нүктелері деп аталады?
№9- дәріс. Бір айнымалы функциялардың дифференциалдық есептеулері. Функцияның туындысы
Айталық,
![]() функциясы
функциясы
![]() нүктесінде және оның маңайында анықталған
болсын.
нүктесінде және оның маңайында анықталған
болсын.
Анықтама.
Аргумент
![]() -тің
-тің
![]() нүктесіндегі
өсімшесі деп
нүктесіндегі
өсімшесі деп
![]() айырмасын атайды.
айырмасын атайды.
Анықтама.
![]() функцияның
нүктесіндегі өсімшесі
деп
функцияның
нүктесіндегі өсімшесі
деп
![]() айырмасын айтады .
айырмасын айтады .
Анықтама.
Егер
![]() функциясы
нүктесінің маңайында
анықталған және
функциясы
нүктесінің маңайында
анықталған және
![]() болса, онда
ол
нүктесінде үзіліссіз
деп аталады. Шындығында
да
болса, онда
ол
нүктесінде үзіліссіз
деп аталады. Шындығында
да
![]()
![]()
![]() .
.
Анықтама.
функциясының
![]() нүктесіндегі туындысы деп
нүктесіндегі туындысы деп
![]() ақырлы
шегін айтады.
ақырлы
шегін айтады.
Бұл
туынды мына символдардың бірімен
белгіленеді:![]() .
.
Егер
![]() функциясының
функциясының
![]() интервалының әрбір нүктесінде туындысы
болса, онда оны осы интервалда
дифференциалданады дейді. Туындыны
табу амалын дифференциалдау дейді.
интервалының әрбір нүктесінде туындысы
болса, онда оны осы интервалда
дифференциалданады дейді. Туындыны
табу амалын дифференциалдау дейді.
Теорема.
Егер
![]() функциясы
нүктесінде
дифференциалданатын функция болса,
онда ол бұл нүктеде
үзіліссіз болады.
функциясы
нүктесінде
дифференциалданатын функция болса,
онда ол бұл нүктеде
үзіліссіз болады.
Ескерту: теорема керісінше дұрыс емес.
Туындының
геометриялық мағанасы.
Туындының
геометриялық мағынасы:
![]() туындысы
функциясының графигіне
туындысы
функциясының графигіне
![]() нүктесінде жүргізілген жанаманың
бұрыштық коэффициенті болады. Осы
жанаманың теңдеуін былай жазады:
нүктесінде жүргізілген жанаманың
бұрыштық коэффициенті болады. Осы
жанаманың теңдеуін былай жазады:
![]() .
Туындының
механикалық мағынасы. Егер
айнымалысын
уақыт деп есептеп,
.
Туындының
механикалық мағынасы. Егер
айнымалысын
уақыт деп есептеп,
![]()
функциясы дененің жүрген жолын сипаттаса,
онда
функциясы дененің жүрген жолын сипаттаса,
онда
![]() дененің
уақытындағы
жылдамдығын білдіреді.
дененің
уақытындағы
жылдамдығын білдіреді.
Дифференциалдаудың негізгі ережелері. Туындының анықтамасын пайдаланып, кейбір элементар (қарапайым) функциялардың туындыларын есептейміз.
Көрсеткішті функция
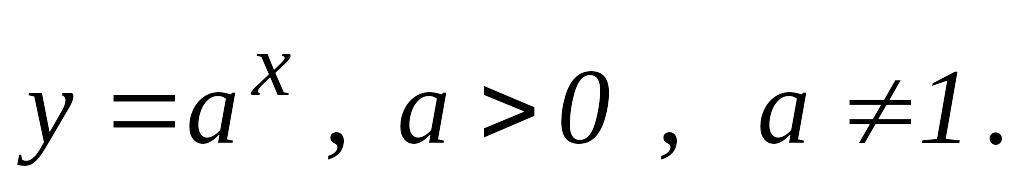
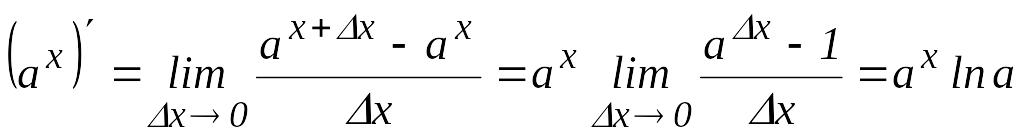 .
Дербес жағдайда
.
Дербес жағдайда
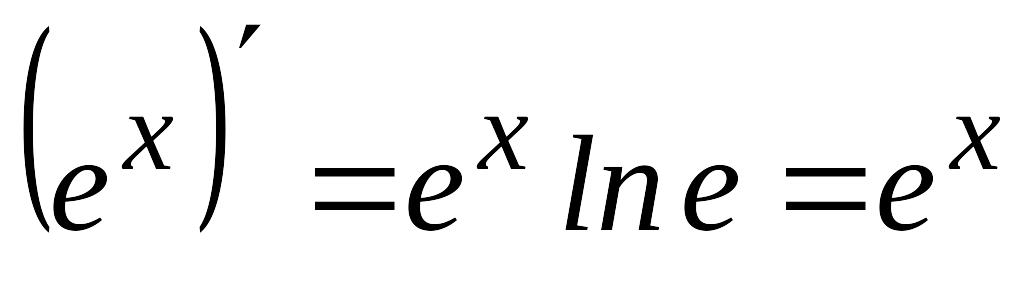 .
.
2.
Тригонометриялық функциялар
![]() .
.
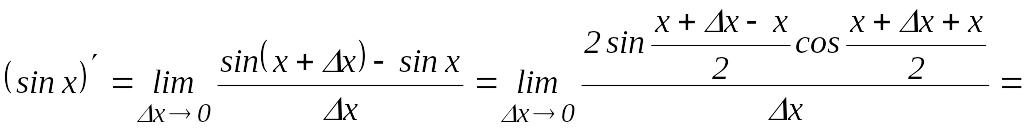
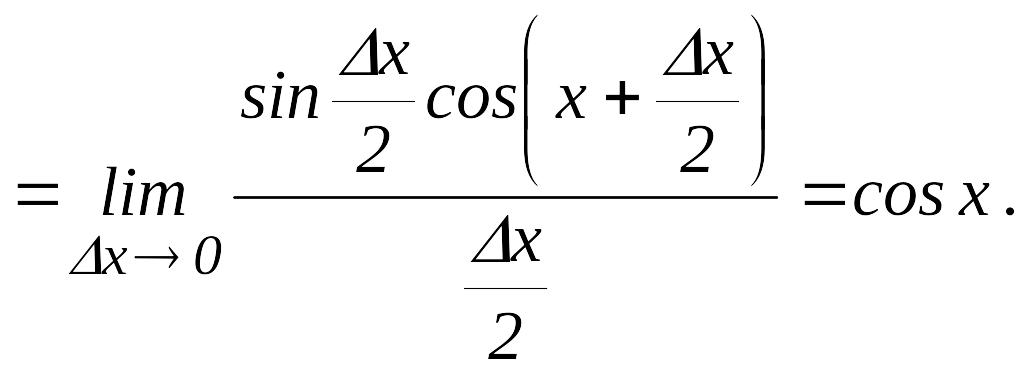 Дәл
осылай
Дәл
осылай
![]() .
.
Дәрежелік функция
 .
.
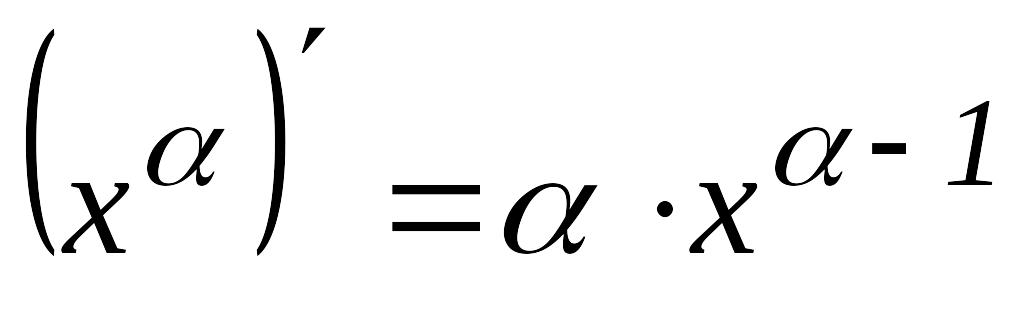
Дербес
жағдайда,
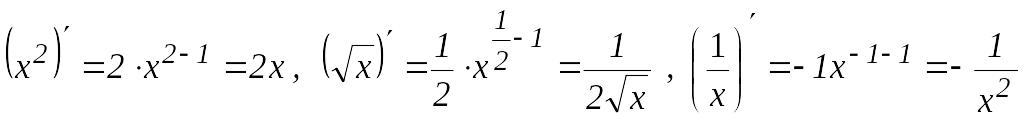 .
.
Теорема
1. (қосындыны,
көбейтіндіні және қатынасты дифференциалдау
ережелері). Егер
![]() және
және
![]() дифференцианалданатын болса, онда бұл
функциялардың қосындысы, көбейтіндісі
және қатынасы да (қатынастың бөлімі
дифференцианалданатын болса, онда бұл
функциялардың қосындысы, көбейтіндісі
және қатынасы да (қатынастың бөлімі
![]() )
осы нүктеде дифференцианалданады және
мына формулалар орынды:
)
осы нүктеде дифференцианалданады және
мына формулалар орынды:
1.
![]() 2.
2.
![]() 3.
3.
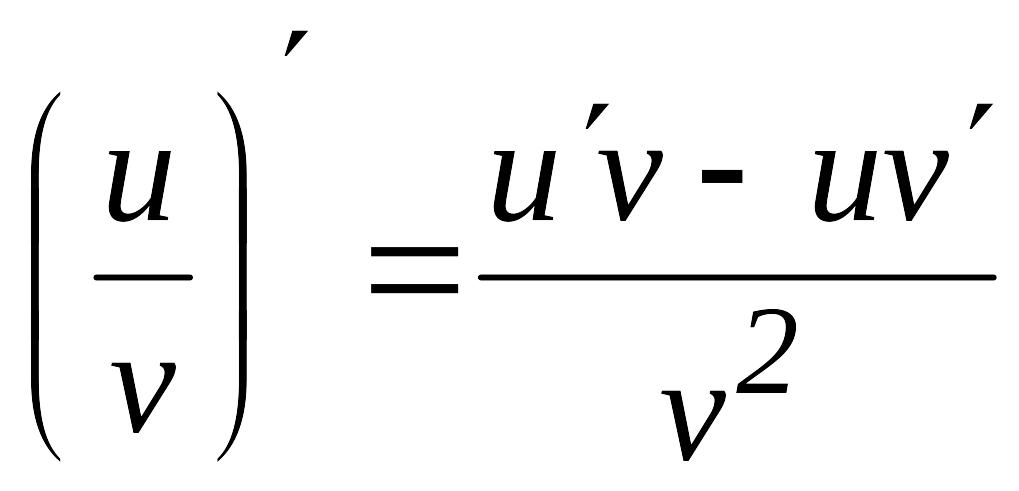 .
.
Күрделі
функцияның туындысы.
![]() функциялары үзіліссіз және
дифференциалданатын функциялар болсын.
Сонда күрделі
функциялары үзіліссіз және
дифференциалданатын функциялар болсын.
Сонда күрделі
![]() функциясының туындысы:
функциясының туындысы:
![]() .
Сонымен
.
Сонымен
![]() .
.
мысал.
![]()
![]() туындысын
табу керек. Функцияны былай жазамыз
туындысын
табу керек. Функцияны былай жазамыз
![]() ,
мұндағы
,
мұндағы
![]() .
Сондықтан
.
Сондықтан
![]() .
.
мысал.
![]() туындысын табу керек.
туындысын табу керек.
![]() .
.
Кері
функцияның туындысы.
![]() және оған кері
және оған кері
![]() функциялары
функциялары
![]() кесіндісінде үзіліссіз және
дифференциалданатын болсын. Сонда кері
функцияның туындысы:
кесіндісінде үзіліссіз және
дифференциалданатын болсын. Сонда кері
функцияның туындысы:
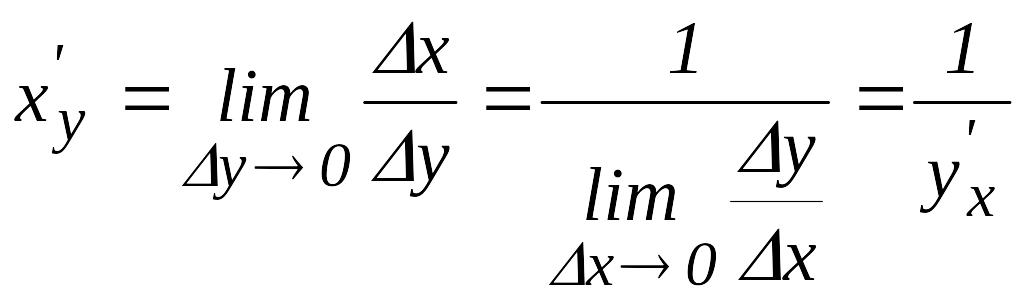 .
Сонымен
.
Сонымен
![]() болады.
болады.
мысал.
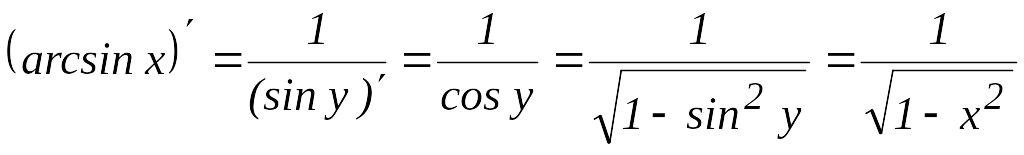 .
.
Мұнда
![]() .
.
![]() .
.
мысал.
![]() .
.
Негізгі элементар функциялар туындыларының кестесі
|
|
Осы кесте мен туындыны есептеу ережелерінің жәрдемімен кез келген функциялардың туындысын табуға болады.