
- •Механика - математика факультеті Дифференциалдық теңдеулер және басқару теориясы кафедрасы
- •Пәннің оқу-әдістемелік кешені Математика
- •Алматы 2013ж. Поәк дайындаған Елдесбай т. Ф.-м.Ғ.Д, профессор
- •Факультеттің әдістемелік (бюро) кеңесінде ұсынылды.
- •1. Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі
- •2. Түзудің жалпы теңдеуі
- •6. Берілген нүктеден өтетін түзудің теңдеуі
- •1. Берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі
- •2. Жазықтықтың жалпы теңдеуі
- •4. Жазықтықтың кесінділік теңдеуі
- •6. Нүктеден түзуге дейінгі қашықтық
- •2. Түзудің канондық теңдеуі
- •2. Эллипс
- •3. Гипербола
- •4. Парабола
- •5. Екінші ретті қисықтың жалпы теңдеуі
- •3. Kонус
- •7. Екі қуысты гиперболоид:
- •2. Аралықта өсетін және кемитін функциялар
- •3. Жұп және тақ функциялар.
- •Бірінші тамаша шек. Құрамында тригонометриялық функциялар бар өрнектердің шектерін есептегенде бірінші тамаша шекті қолданады: . Дәлелдеу: Радиусы бірге тең шеңбер аламыз. , сонда:
- •Екінші тамаша шек: .
- •Kесіндіде үзіліссіз функциялардың қасиеттері
- •Параметр арқылы берілген функцияның туындысы. Функциясын кейде параметрлік түрде жазған ыңғайлы болады
- •Дифференциалды есептеу формулаларын келтірейік:
- •Анықталған интегралдың анықтамасы. Функциясы кесіндісінде анықталсын, мұнда . Төменгі амалдарды орындаймыз.
- •3−Мысал.
- •3. Қисық доғасының ұзындығы
- •2. Ақырсыз функцияның меншіксіз интегралы
- •2.3 Тәжірибелік (семинар) сабақтарының жоспары.
- •2.4 Оқытушының жетекшілігімен орындалатын студенттердің өзіндік жұмыстары бойынша өткізілетін сабақтардың жоспары (соөж)
- •2.5. Студенттердің өздік жұмыстары бойынша сабақ жоспары (сөж)
- •2.6. Курс бойынша жазбаша жұмыстың тақырыптары
- •2.7. Өздік бақылау үшін тест тапсырмалары
- •2.8. Курс бойынша емтихандық сұрақтар
ӘЛ-ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
Механика - математика факультеті Дифференциалдық теңдеулер және басқару теориясы кафедрасы
Келісілген: Факультет деканы _______________ А.Б.Қыдырбекұлы "_______"___________ 2013 ж.
|
Университеттің ғылыми-әдістемелік кеңесінде бекітілді Хаттама №__ «__»__ 2013 ж. Оқу жұмысы жөніндегі проректор _________________ Д.Ж. Ахмет-Заки "____"______ 2013 ж. |
Пәннің оқу-әдістемелік кешені Математика
(пәннің аты)
Мамандық «5В070100-Биотехнология»
(шифры, аты)
Оқу түрі күндізгі бөлім
(күндізгі, сырттай)
Алматы 2013ж. Поәк дайындаған Елдесбай т. Ф.-м.Ғ.Д, профессор
Элективті пән бойынша: « Оқу-әдістемелік кешен тәжірибелік білім бағдарламасы және «Биотехнология» мамандығының Элективті пәндер каталогы негізінде әзірленді».
Дифференциалдық теңдеулер және басқару теориясы кафедрасының
мәжілісінде қаралып ұсынылды.
«___ » __________________ 2013 ж., хаттама №____
Кафедра меңгерушісі _________________ С.Т. Мухамбетжанов
Факультеттің әдістемелік (бюро) кеңесінде ұсынылды.
« ___ » _____________ 2013 ж., хаттама № __
Төрағасы (Төрайымы) _________________ Ж.Б.Байтуленов
Алғы сөз
Математика қазіргі таңдағы көптеген ғылыми салаларындағы қолданылатын әдістердің теориялық фундаменті болып табылады. Бұл әрине, компьютерлік технологияның онан әрі дамуына байланысты, математиканың қолдану ауқымы кеңейе түсуде.
Курстың мазмұны: сызықтық алгебра және аналитикалық геметрия элементтері. Математикалық анализ: бір айнымалы функцияның дифференциалдық және интегралдық есептеулері.
Курстың мақсаты: студенттерді негізгі математикалық ұғымдарда кезігетін математикалық әдістермен таныстыру. Оқу процесінде кезігетін арнайы курстар мен өз бетінше математиканы қолдану бағытында кезігетін әдістерді игеруге негіз салу.
Курстың міндеттері: жоғары математиканың негізгі ұғымдарын және жер құрылыс саласындағы оны қолдануын оқып білу. Математикалық моделдер туралы түсінік беру және оларды жүзінде қолдана білу.
Студенттер бойында келесі біліктіліктер қалыптасуы керек: бөлінген кредит мөлшерінде өзінің математикалық біліктілігін ұштай отырып, жоғарғы математикадағы оқылатын математикалық ұғымдармен әдістерді жете меңгеріп, өз мамандығында оларды қолдана білетін дәрежеге жетуі тиіс.
Игеруі керек: бір айнымалы функцияның дифференциалдық және интегралдау есептеулерін және меңгеріп, сонымен қатар олардың қолдануларын меңгеру тиіс. Кейбір математикалық моделдерді оқып, олардың қолдану ауқымын білуі тиіс.
Қалыптасатын дағдылары: сабаққа ауқытымен келіп, берілген тапсырмаларды орындап, тиісті балдарын тиянақты түрде тырнақтап жинауды үйрену.
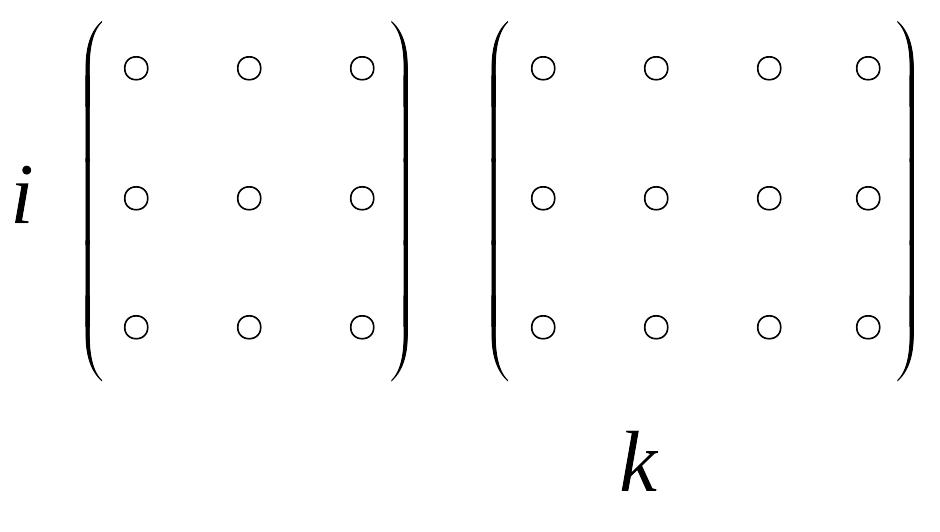
№1-дәріс. Матрицалар және анықтауыштар. Матрицалар
Матрица деп, m- жол және n- бағаннан тұратын сандар немесе әріптерден құрылған тік бұрышты кестені айтады.
Матрица латынның үлкен әріптерімен белгіленеді A,B,C,… және былай жазылады:
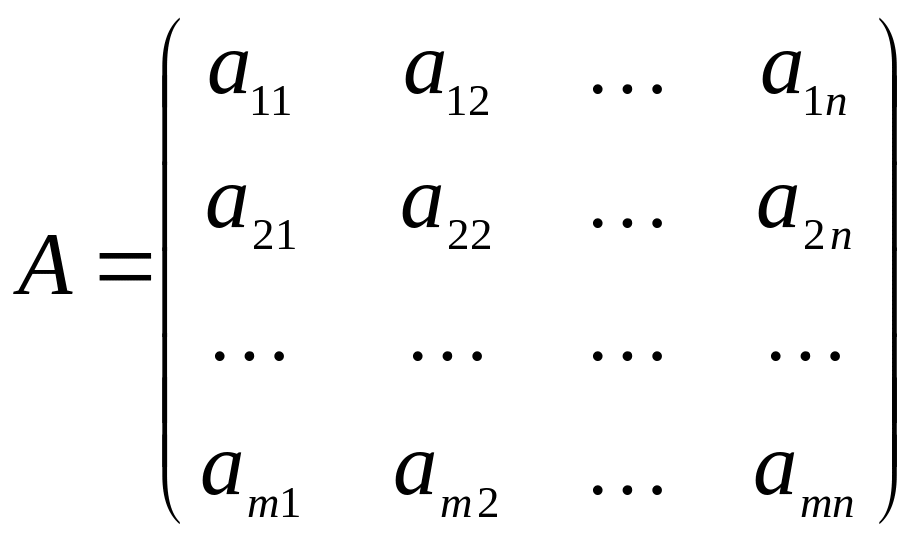
немесе
қысқаша
![]() ,
мұндағы
,
мұндағы
![]() (яғни
(яғни
![]() )
– жолдың нөмірі,
)
– жолдың нөмірі,
![]() (яғни
(яғни
![]() )
– бағанның нөмірі.
)
– бағанның нөмірі.
А
матрицасын
![]() өлшемді матрица дейді және оны
өлшемді матрица дейді және оны
![]() деп жазады. Матрицаны құрайтын
деп жазады. Матрицаны құрайтын
![]() сандарын сол матрицаның элементтері
дейді.
сандарын сол матрицаның элементтері
дейді.
![]() элементтері бас диагоналді құрайды.
элементтері бас диагоналді құрайды.
![]() -
-
![]() -
өлшемді матрица.
-
өлшемді матрица.
Бір
жолдан тұратын матрицаны жол-матрица
дейді. Бір бағаннан тұратын матрицаны
баған-матрица
дейді. Егер матрицаның жолдарының саны
бағандарының санына тең болса, ондай
матрицаны квадрат
матрица дейді.
Оның өлшемі
![]() болады.
болады.
Егер квадрат матрицаның бас диагональдан тыс элементтері нөлге тең болса, онда ондай матрицаны диагональ матрица дейді.
Егер диагональ матрицаның бас диагоналі бір сандарынан тұрса, онда ондай матрицаны бірлік матрица дейді және оны Е деп белгілейді.
Егер квадрат матрицаның бас диагоналінің бір жағына орналасқан элементтері түгелдей нөлге тең болса, онда оны үшбұрышты матрица дейді.
Егер матрицаның барлық элементтері нөлге тең болса, онда ондай матрицаны
нөлдік матрица дейді. Мысалы. а) квадрат; б) диагональ; в) бірлік; г) нөлдік матрицалар:
а)
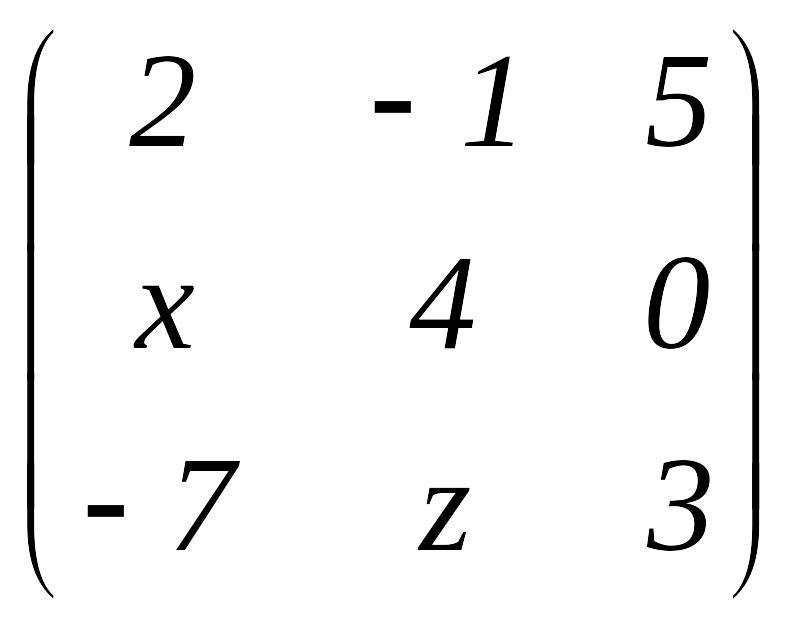 ;
б)
;
б)
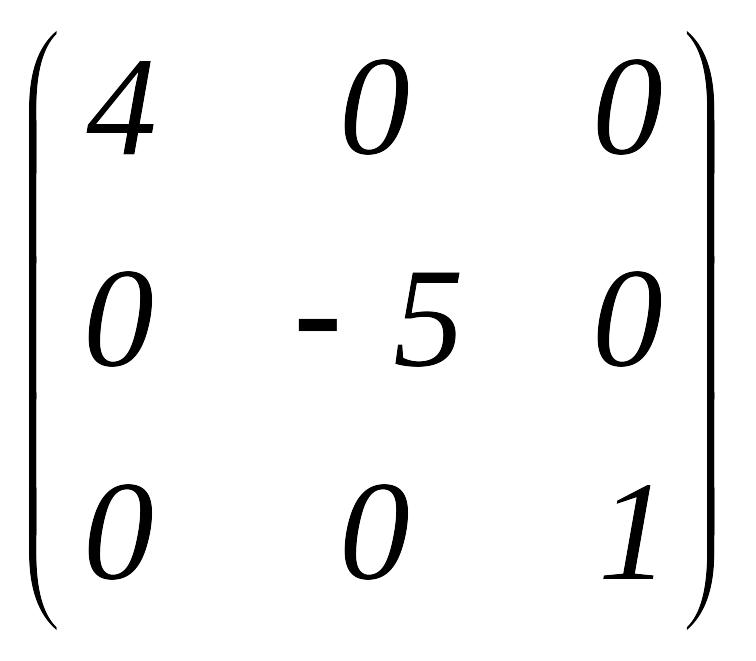 ;
в)
;
в)
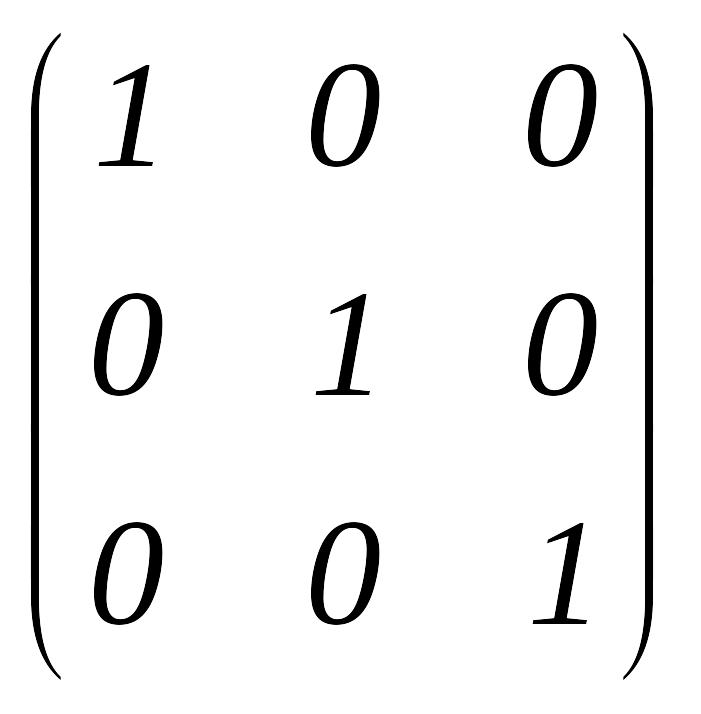 ;
г)
;
г)
![]() .
.
А
матрицасының жолдарын сәйкес бағандар
етіп алмастырғаннан пайда болған
матрицаны транспонирленген
матрица деп атайды
және оны
![]() деп
белгілейді. Транспонирлеу амалының
қасиеттері:
деп
белгілейді. Транспонирлеу амалының
қасиеттері:
![]()
![]()
1-мысал.
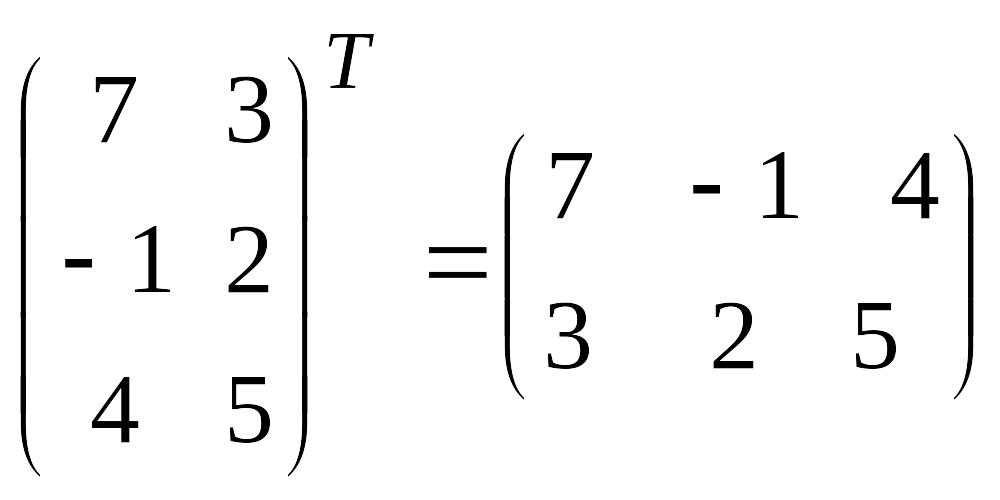
Матрицаларға
амалдар қолдану. Қосу
амалы амалы өлшемдері бірдей матрицалар
үшін ғана енгізіледі. Екі
![]() және
және
![]() матрицаларының
қосындысы деп,
элементтері
матрицаларының
қосындысы деп,
элементтері
![]() болатын
болатын
![]() матрицасын айтады және оны
матрицасын айтады және оны
![]() деп белгілейді.
деп белгілейді.
2-мысал.
![]() матрицасын
матрицасын
![]() санына көбейту деп
әрбір элементі
санына көбейту деп
әрбір элементі
![]() болатын
матрицасын айтады.
болатын
матрицасын айтады.
3-мысал.
![]() -А=(-1)А
матрицасын А матрицасына
қарама-қарсы матрица
деп атайды. Олай болса, матрицалардың
айырымын былай анықтауға болады:
-А=(-1)А
матрицасын А матрицасына
қарама-қарсы матрица
деп атайды. Олай болса, матрицалардың
айырымын былай анықтауға болады:
![]()
Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері:
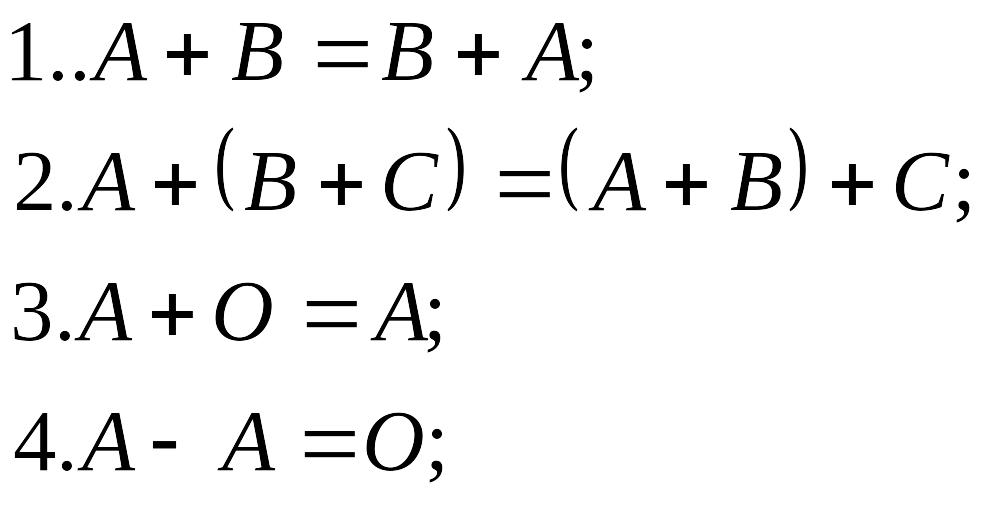
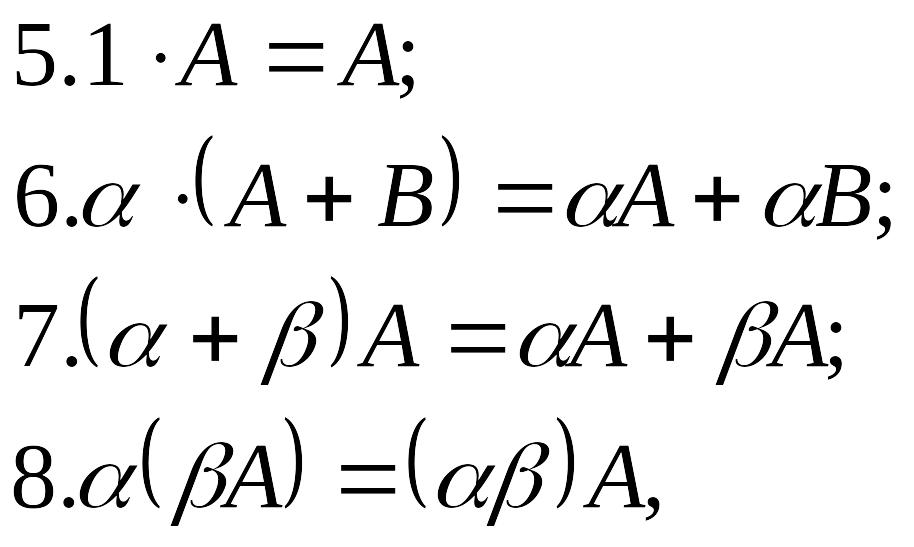
мұндағы
![]() матрицалар,
матрицалар,
![]() және
және
![]() -
сандар.
-
сандар.
Екі
матрицаны көбейту амалы бірінші
матрицаның бағандарының саны екінші
матрицаның жолдарының санына тең
болғанда ғана енгізіледі.
![]() матрицасының
матрицасының
![]() матрицасына көбейтіндісі деп элементтері
матрицасына көбейтіндісі деп элементтері
![]() ,
,
,
,
![]()
болатын
![]() матрицасын айтады. Схемалық түрде былай
көрсетуге болады:
матрицасын айтады. Схемалық түрде былай
көрсетуге болады:


4-мысал.![]() ,
,
![]()
![]()
![]() ,
осыдан
,
осыдан
![]()
Егер
![]() болса, онда А және
В матрицалары
алмастырылатын
матрицалар деп
аталады.
болса, онда А және
В матрицалары
алмастырылатын
матрицалар деп
аталады.
Матрицаларды көбейту амалының қасиеттері:
![]()
![]()
Анықтауыштар. Анықтауыш сатылы түрде анықталады.
1) Кезкелген сан бірінші ретті анықтауыш.
2)
Өлшемділігі 2-ге тең квадрат матрица
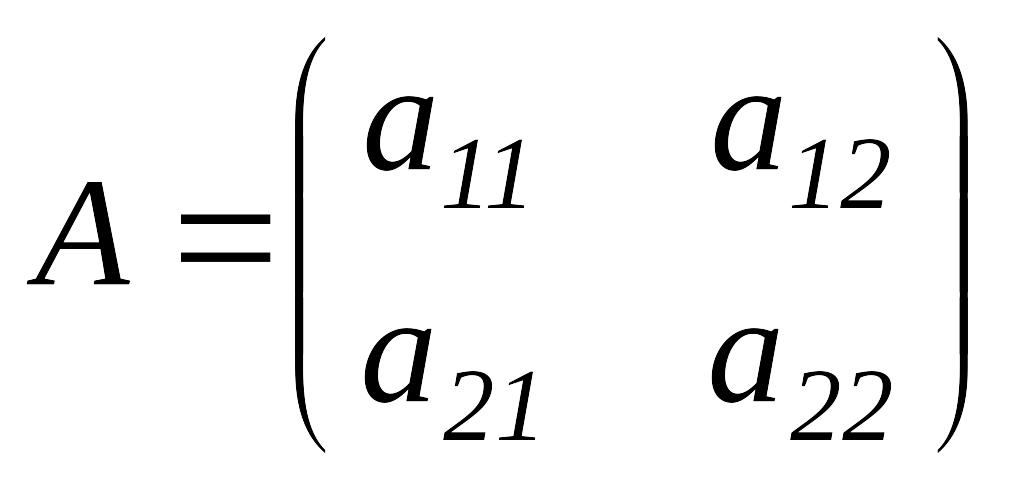 үшін
үшін
![]() саны (мұндағы
саны (мұндағы
![]() - нақты сандар)
А матрицасының анықтауышы немесе 2-ші
ретті анықтауыш деп
аталады және ол
- нақты сандар)
А матрицасының анықтауышы немесе 2-ші
ретті анықтауыш деп
аталады және ол
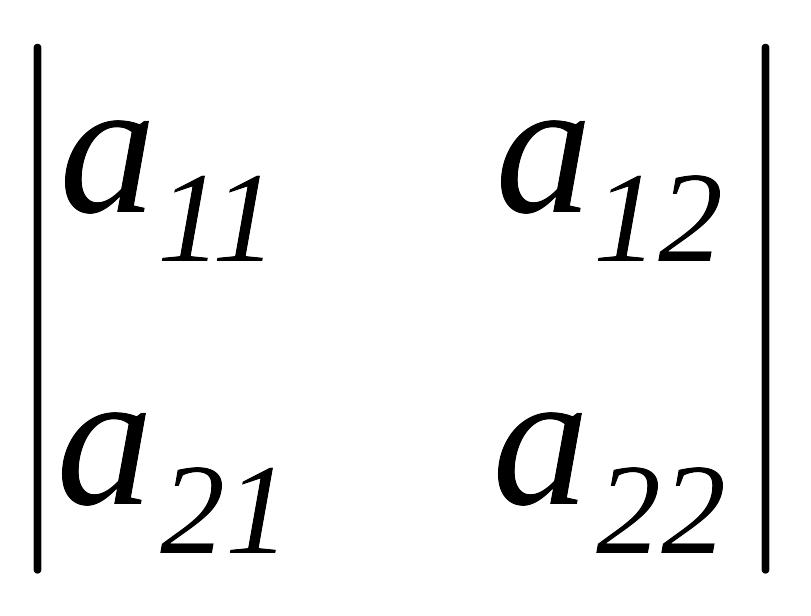 ,
,
![]() ,
,
![]() ,
,
![]() деп белгіленеді. Сонымен
деп белгіленеді. Сонымен
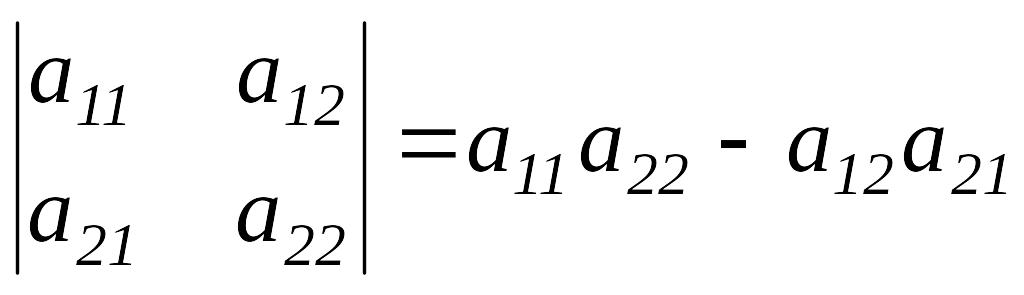
5-мысал.
![]()
3)
 -
3-ші ретті матрица болсын.
-
3-ші ретті матрица болсын.
А матрицасының анықтауышы немесе 3-ші ретті анықтауышы деп, төменгі формуламен есептелінетін санды айтады:
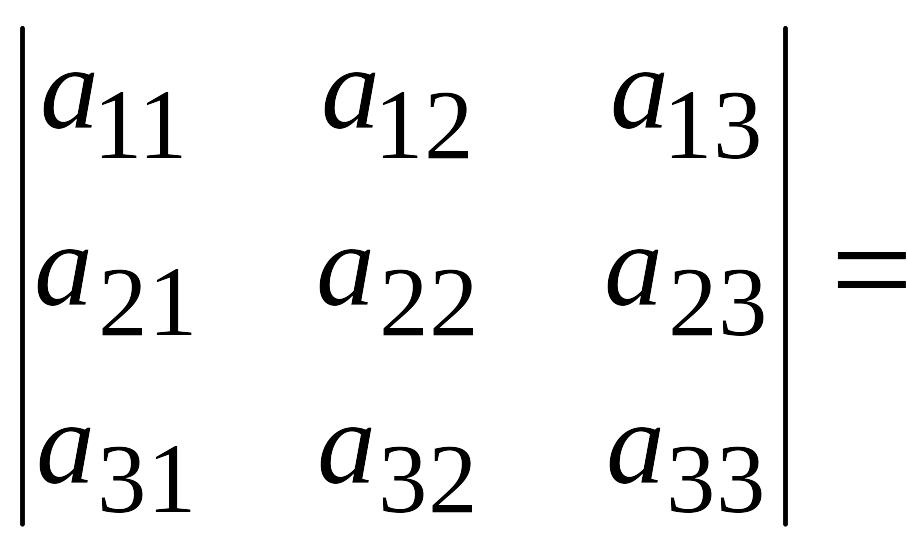
![]()
![]() .
.
Б


 ұл
формуланы жеңіл есте сақтау үшін алғашқы
оң таңбалы үш қосылғышты
ұл
формуланы жеңіл есте сақтау үшін алғашқы
оң таңбалы үш қосылғышты
 схемасы бойынша, ал қалған үш теріс
таңбалы қосылғыштарды схемасы
бойынша есептелетіндігін ескеру қажет.
схемасы бойынша, ал қалған үш теріс
таңбалы қосылғыштарды схемасы
бойынша есептелетіндігін ескеру қажет.
4 )
)
 квадрат
матрицасының
элементінің
миноры деп, осы элемент
орналасқан жол мен бағанды сызып
тастағаннан шығатын 3-ші ретті анықтауышты
айтады және оны
квадрат
матрицасының
элементінің
миноры деп, осы элемент
орналасқан жол мен бағанды сызып
тастағаннан шығатын 3-ші ретті анықтауышты
айтады және оны
![]() деп белгілейді. Ал
деп белгілейді. Ал
![]() саны
элементінің алгебралық
толықтауышы деп
аталады. Онда
саны
элементінің алгебралық
толықтауышы деп
аталады. Онда
![]() саны 4-ші ретті анықтауыш деп аталады
және ол
саны 4-ші ретті анықтауыш деп аталады
және ол
 түрінде белгіленеді. Дәл осылай 5-ретті
анықтауыш анықталады:
түрінде белгіленеді. Дәл осылай 5-ретті
анықтауыш анықталады:
![]() (1.1)
(1.1)
Осылайша
кезкелген
![]() -ші
ретті анықтауышты
-ші
ретті анықтауышты
![]() -ші
ретті анықтауыштар арқылы анықтаймыз.
-ші
ретті анықтауыштар арқылы анықтаймыз.
(1.1) формуласы анықтауышты кез келген жолдың элементтері арқылы жіктеу деп аталады.
6-мысал.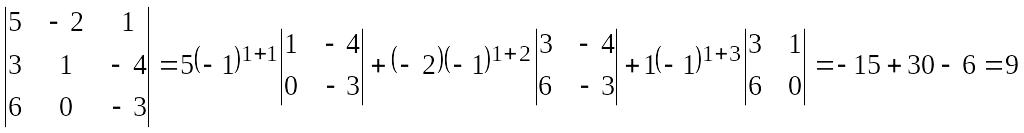
Анықтауыштың қасиеттері:
1. Анықтауыштың жолдарын сәйкес бағандармен алмастырғаннан анықтауыштың мәні өзгермейді.
2. Егер анықтауыштың қандай да бір жолы (бағаны) тек нөлден тұрса, онда анықтауыш нөлге тең.
3.Егер анықтауыштың екі жолы (бағаны) пропорционал болса, онда анықтауыш нөлге тең.
4. Жолдың (бағанның) ортақ көбейткішін анықтауыштың алдына шығарып жазуға болады.
5.Егер анықтауыштың екі жолын (бағанын) алмастырса, онда анықтауыштың таңбасы өзгереді.
6. Егер қандай да бір жолдың (бағанның) элементтеріне кез келген санға көбейтілген басқа жолдың сәйкес элементтерін қосқаннан анықтауыш өзгермейді.
Әдебиеттер: 1 нег.[5-20], 11 қос. [92-115]
Бақылау сұрақтар:
1. Екінші ретті анықтауыш деген не? 4-ретті анықтауыш деген не? Анықтауыштардың
негізгі қасиеттерін атаңыз.
2. Матрицаның анықтауыштан айырмашылығы неде? Матрицаларға қолданылатын амалдарды атаңыз.
3. Екі матрицаны көбейту қай кезде орындалады?
№2-дәріс. Сызықтық алгебралық теңдеулер жүйесі. Матрицаның рангі
А
матрицасының рангі
деп осы матрицаның нөлге тең емес
минорларының ең үлкен ретін айтады және
оны
![]() ,
,
![]() немесе
немесе
![]() деп
белгілейді.
деп
белгілейді.
![]() болады,
мұндағы
болады,
мұндағы
![]() -
m және n сандарының кішісі.
-
m және n сандарының кішісі.
1-мысал. матрицасының
рангін табыңыз.
матрицасының
рангін табыңыз.
1-әдіс. Минорлар әдісі. Бұл матрицаның рангі 3-тен аспайды. Сондықтан 3-ші ретті минорлар құрамыз. Егер 3-ші ретті минорлардың ішінде бір нөлге тең емес минор табылса, онда ранг 3-ке тең болады. Ал 3-ші ретті минорлардың бәрі нөлге тең болса, онда минор 2-ге не 1-ге тең болады. Оны білу үшін тағы 2-ші ретті минорлар құрамыз. Олардың ішінде бір нөлге тең емес минор табылса, онда ранг 2-ге тең болады. Ал 2-ші ретті минорлардың бәрі нөлге тең болса, минор 1-ге тең.
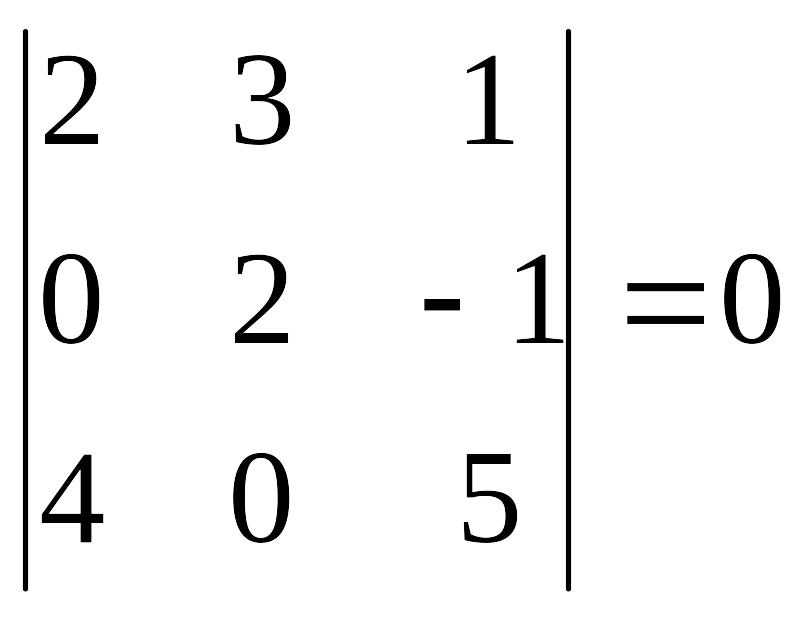 ,
,
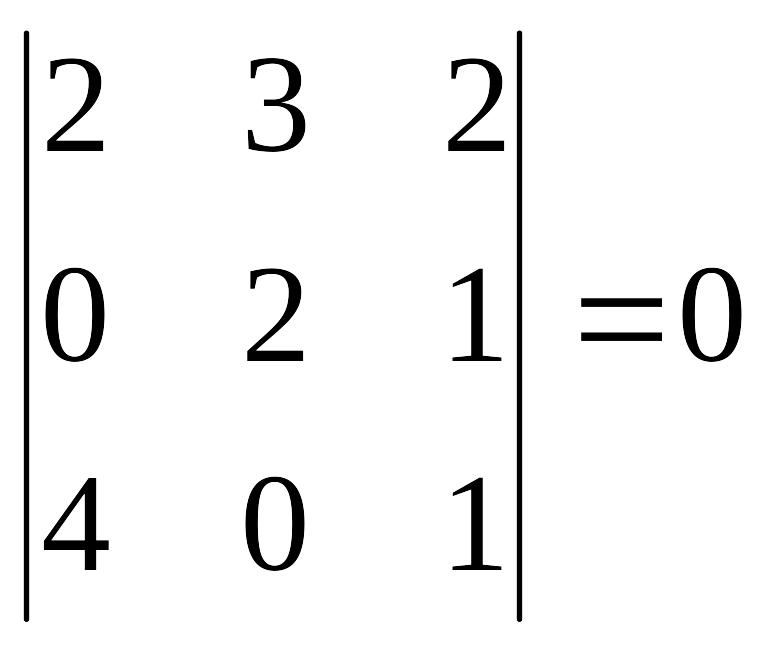 ,
3-ші ретті минорлардың бәрі нөлге тең.
Олай болса, 2-ші ретті минорлар құрамыз:
,
3-ші ретті минорлардың бәрі нөлге тең.
Олай болса, 2-ші ретті минорлар құрамыз:
![]() .
Демек ранг 2-ге тең, яғни
.
Демек ранг 2-ге тең, яғни
![]()
2-әдіс. Элементар түрлендіру әдісі. Матрицаны элементар түрлендіру деп:
1. матрицаның екі жолын (бағанын) ауыстыру;
2. матрицаның жолын (бағанын) нөлге тең емес санға көбейту;
3. бір жол (баған) элементтеріне басқа жолдың (бағанның) сәйкес қандай да бір санға көбейтілген элементтерін қосу амалдарын айтады.
Элементар түрлендіру арқылы алынған матрицаны бастапқы матрицаға эквивалентті матрица дейді және орталарына ~ белгісі қойылады. Матрицаның рангін табу үшін элементар түрлендіруді пайдаланып, матрицаны сатылы түрге келтіреміз.
Теорема. Матрицаны элементар түрлендіргеннен оның рангі өзгермейді.
2-мысал.
~
 ~
~
 .
Демек ранг 2-ге тең, яғни
.
.
Демек ранг 2-ге тең, яғни
.
Кері
матрица. Егер
![]() шарты орындалса, онда
шарты орындалса, онда
![]() матрицасын
матрицасын
![]() матрицасына кері матрица
дейді және оны
матрицасына кері матрица
дейді және оны
![]() түрінде белгілейді.
Мұндағы
,
,
түрінде белгілейді.
Мұндағы
,
,
![]() матрицалары бірдей
өлшемді квадрат матрицалар.
матрицалары бірдей
өлшемді квадрат матрицалар.
Ескерту:
Егер
![]() матрицасы бар болса,
онда ол жалғыз болады.
матрицасы бар болса,
онда ол жалғыз болады.
Теорема.
Квадрат А
матрицасына кері
матрица табылуы үшін
![]() болуы қажетті және жеткілікті.
болғанда кері матрица
былайша
есептелінеді
болуы қажетті және жеткілікті.
болғанда кері матрица
былайша
есептелінеді
![]() .
.
Мұндағы
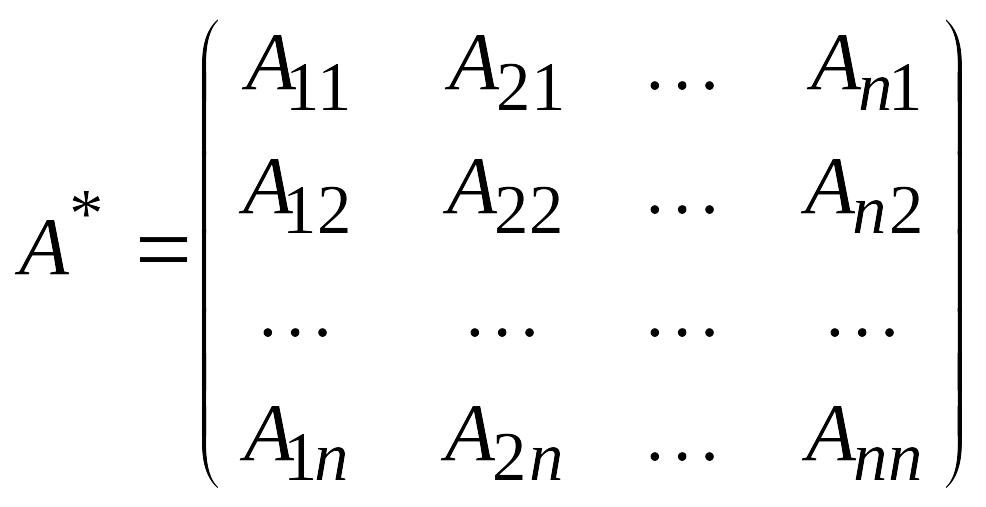 алгебралық толықтауыштардан түзілген
матрица.
алгебралық толықтауыштардан түзілген
матрица.
3-мысал.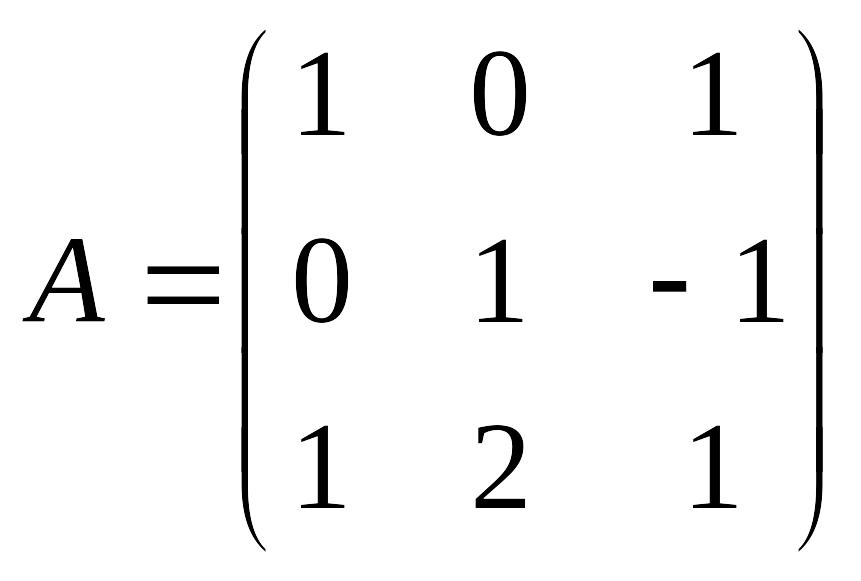 матрицасына
кері матрица табыңыз.
матрицасына
кері матрица табыңыз.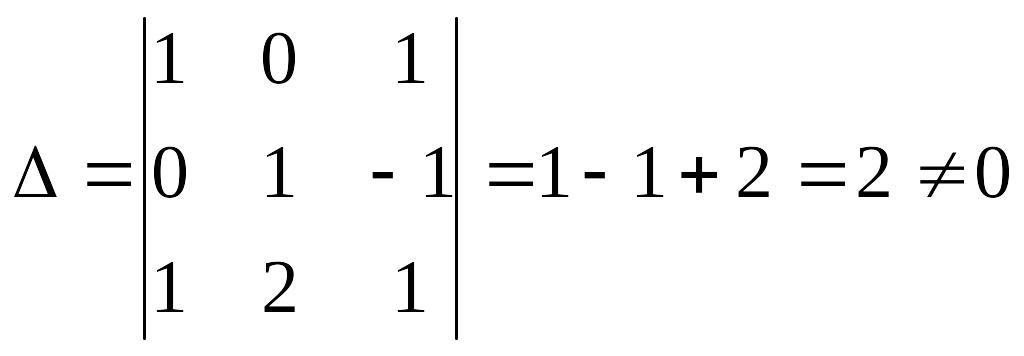 .
.
Олай болса,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Сонда
кері матрица былай болады:
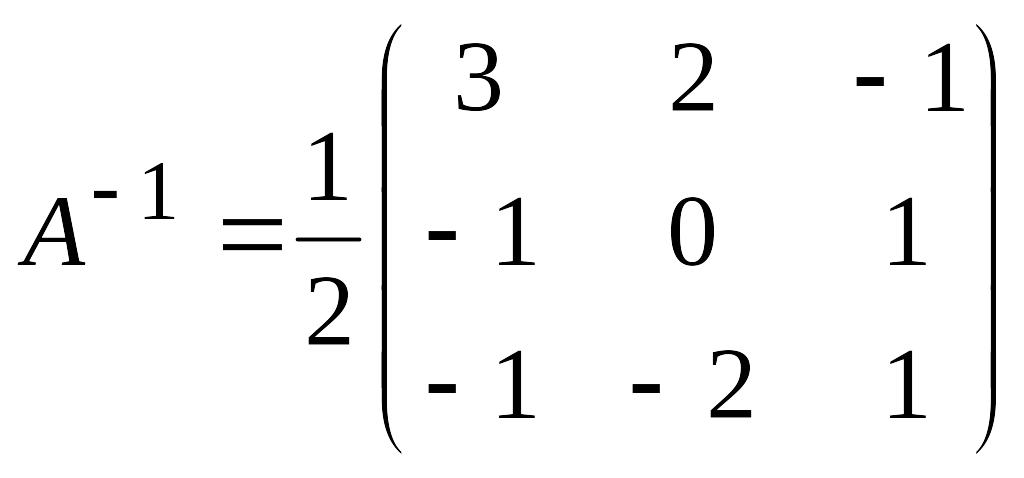 =
=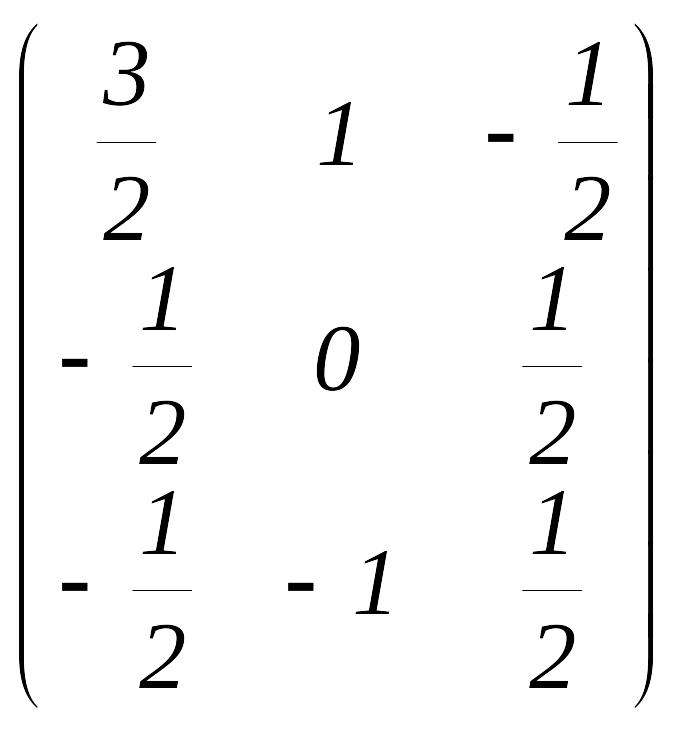 .
.
Сызықтық алгебралық теңдеулер жүйесі. n белгісізі бар m теңдеулер жүйесі былай жазылады:
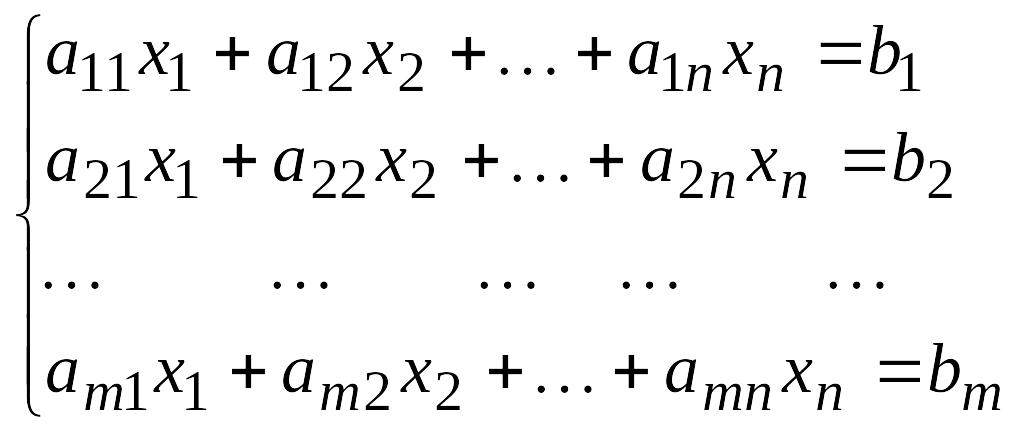
![]()
мұндағы
![]() жүйенің коэффициенттері, ал
жүйенің коэффициенттері, ал
![]() - бос мүшелер деп аталады.
- бос мүшелер деп аталады.
![]() жүйені матрицалық түрде былай жазуға
болады
жүйені матрицалық түрде былай жазуға
болады
![]() немесе
немесе
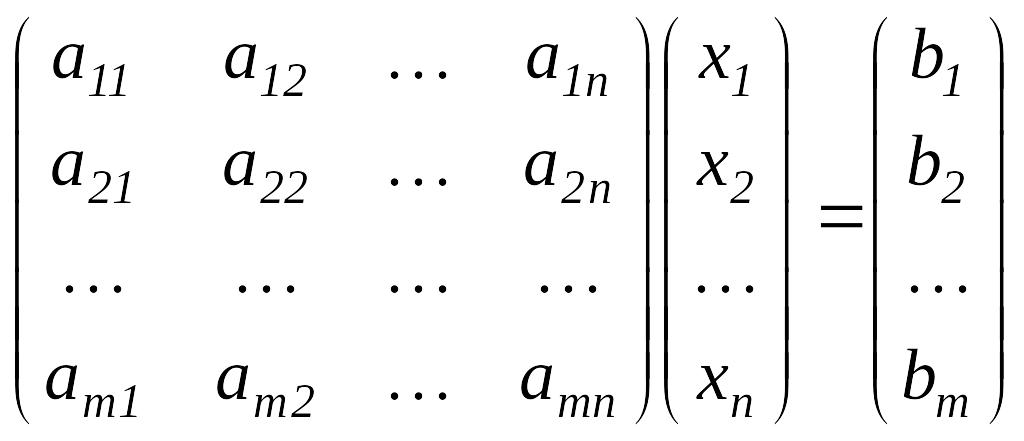 ,
мұндағы А=
,
мұндағы А=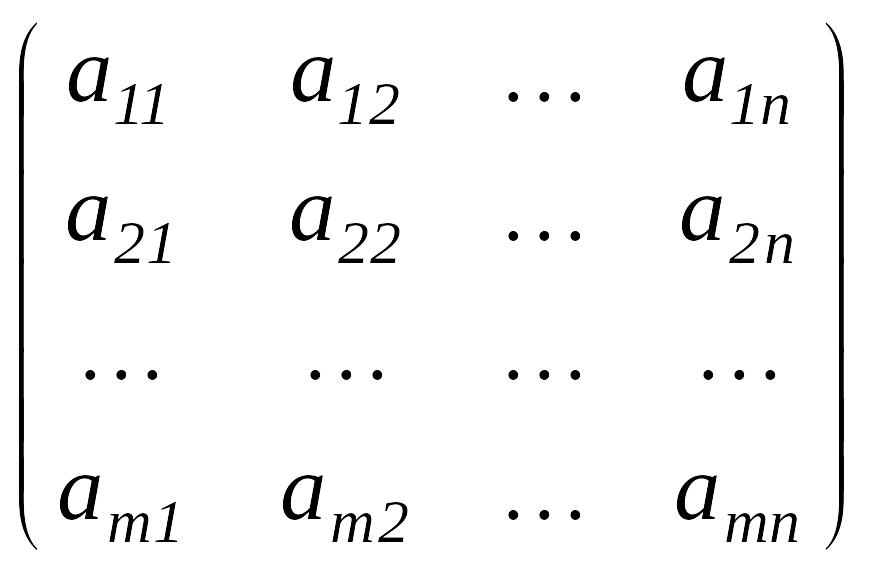 жүйе матрицасы
жүйе матрицасы

A X B
деп аталады.
Егер
![]() сандар жиыны
теңдеулер жүйесін тепе-теңдікке
айналдырса, онда бұл сандар жиыны осы
жүйенің шешімі
деп аталады.
сандар жиыны
теңдеулер жүйесін тепе-теңдікке
айналдырса, онда бұл сандар жиыны осы
жүйенің шешімі
деп аталады.
Егер теңдеулер жүйесінің кемінде бір шешімі бар болса, онда жүйе үйлесімді деп аталады, ал жүйенің бір де шешімі болмаса, онда жүйе үйлесімсіз деп аталады.
Егер
А
матрицасын бос мүшелерден тұратын
бағанмен толықтырса, онда пайда болған
матрицаны кеңейтілген
матрица дейді және
оны
![]() деп белгілейді. Сонымен
деп белгілейді. Сонымен

Сызықтық теңдеулер жүйесін шешу тәсілдері.
1. Крамер ережесі. n белгісізі бар n теңдеулер жүйесі берілсін

![]()
Мұндай жүйенің А матрицасы квадрат матрица болады.
Теорема.
Егер
жүйесі үшін
![]() болса, онда жүйенің жалғыз шешімі былайша
табылады:
болса, онда жүйенің жалғыз шешімі былайша
табылады:
![]()
![]()
мұнда
![]() -
анықтауышындағы
-
анықтауышындағы
![]() белгісіздерінің коэффициеттерін бос
мүшелермен алмастырғаннан пайда болған
анықтауыш.
Крамер формуласы
деп аталады.
белгісіздерінің коэффициеттерін бос
мүшелермен алмастырғаннан пайда болған
анықтауыш.
Крамер формуласы
деп аталады.
4-мысал.
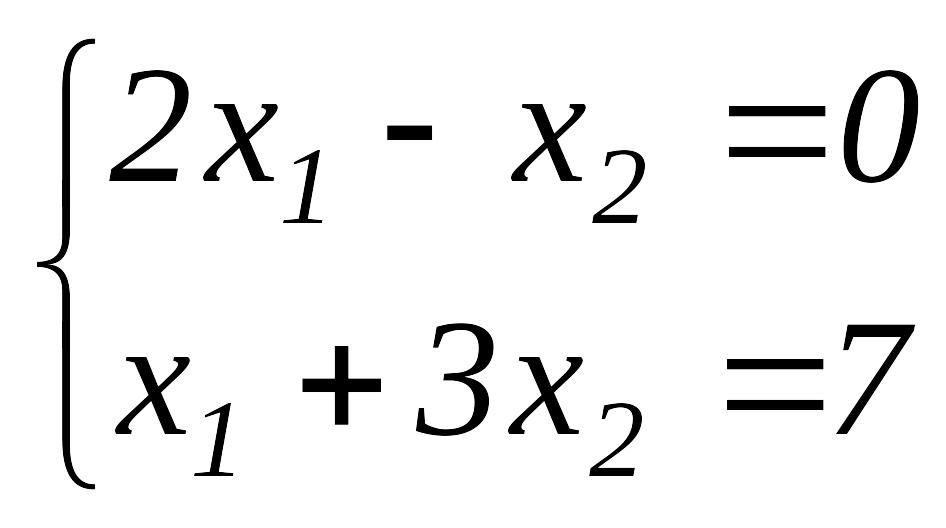 жүйесін Крамер ережесімен шешу керек.
жүйесін Крамер ережесімен шешу керек.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() Жауабы:
Жауабы:
![]()
2. Матрицалық әдіс. n белгісізі бар n теңдеулер жүйесі, яғни жүйе берілсін. Жүйені матрицалық түрде былай жазамыз
Теорема.
Егер
болса, онда
жүйесінің
![]() теңдігімен анықталатын жалғыз шешімі
бар.
теңдігімен анықталатын жалғыз шешімі
бар.
5мысал. жүйесін матрицалық әдіспен шешу керек.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
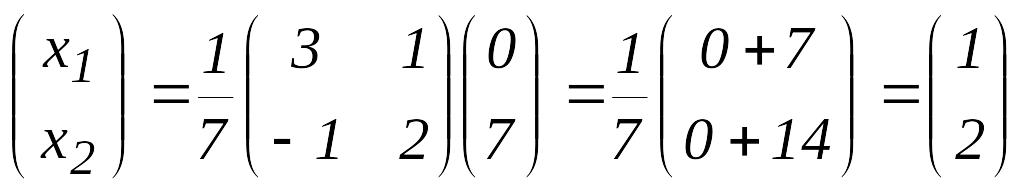 ,
Жауабы:
,
Жауабы:
3. Гаусс әдісі. n белгісізі бар m теңдеулер жүйесі, яғни берілсін. Жүйені Гаусс әдісімен шешу екі кезеңнен тұрады. Бірінші кезеңде (тік жүріс) жүйе трапеция тәріздес түрге келтіріледі.
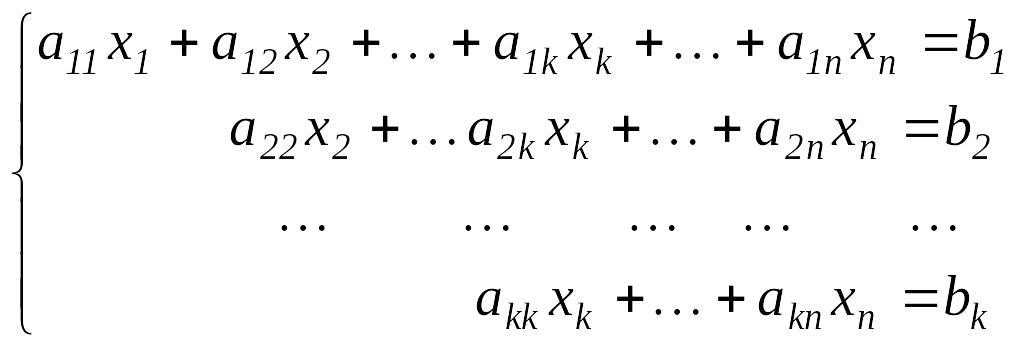 – трапеция
тәріздес жүйе.
– трапеция
тәріздес жүйе.
Мұнда
![]()
![]() коэффициенттері жүйенің негізгі
элементтері деп аталады.
коэффициенттері жүйенің негізгі
элементтері деп аталады.
Екінші
кезіңде (кері жүріс)
мүмкін болса, шыққан жүйеден біртіндеп
белгісіздерді табады. Практикада жүйемен
емес кеңейтілген матрицамен істеген
ыңғайлы болады. Сондықтан жүйені Гаусс
әдісімен шешу үшін кеңейтілген матрица
құрып,оны элементарлық түрлендірудің
көмегімен трапеция тәріздес түрге
келтіреді. Бұл жағдайда
![]() коэффициентінің 1-ге тең болғаны ыңғайлы.
Ол үшін теңдеулердің орындарын ауыстыру
керек немесе теңдеудің екі жағын да
коэффициентінің 1-ге тең болғаны ыңғайлы.
Ол үшін теңдеулердің орындарын ауыстыру
керек немесе теңдеудің екі жағын да
![]() бөлу керек. Содан соң қайтадан жүйе
құрып, сол жүйені шешеміз.
бөлу керек. Содан соң қайтадан жүйе
құрып, сол жүйені шешеміз.
6-мысал.
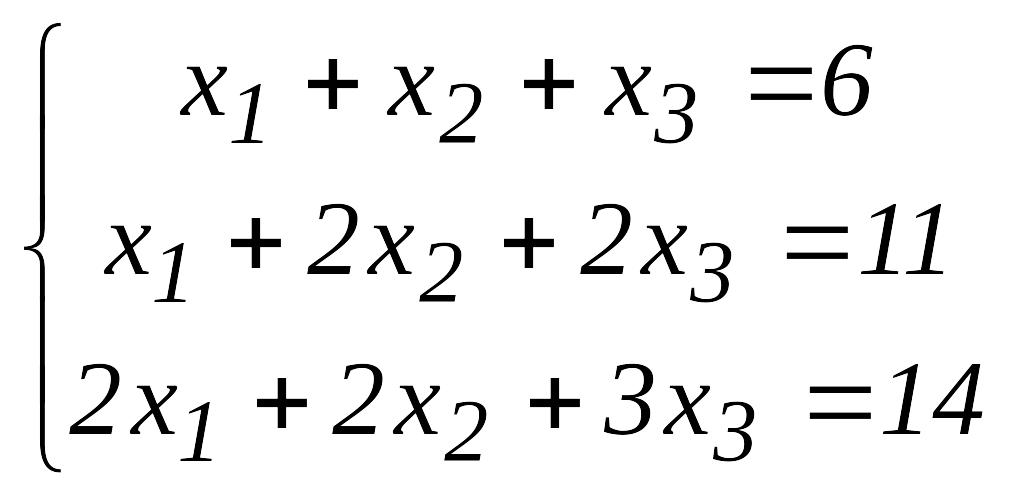 жүйесін Гаусс әдісімен шешу керек.
жүйесін Гаусс әдісімен шешу керек.





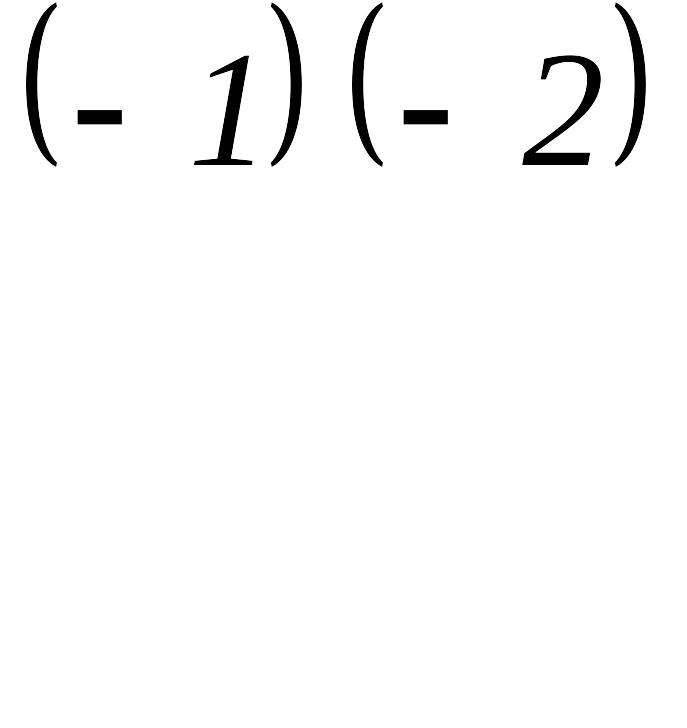 ~
~
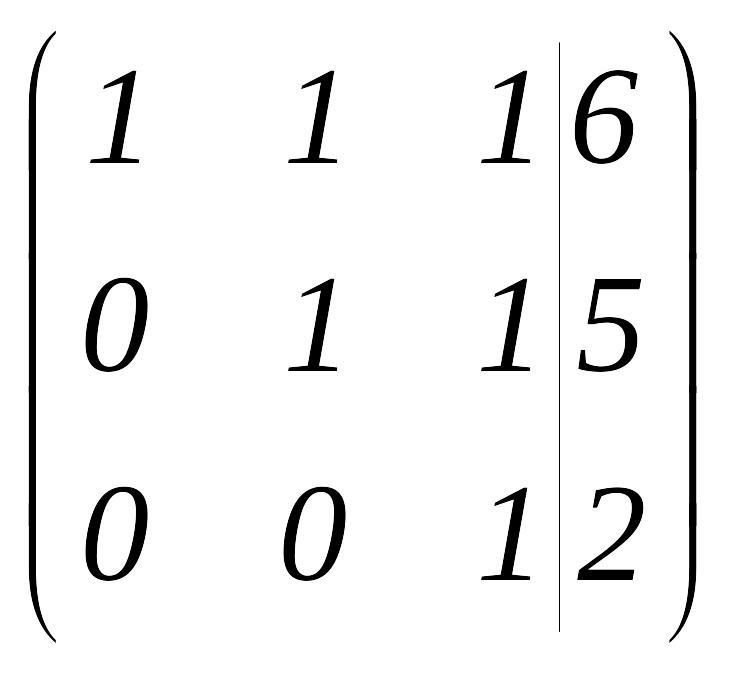 Екінші матрицаның екінші жолын алу үшін
бірінші жолды
Екінші матрицаның екінші жолын алу үшін
бірінші жолды
![]() -ге
көбейтіп, екінші жолға қостық, ал үшінші
жолын алу үшін бірінші жолды
-ге
көбейтіп, екінші жолға қостық, ал үшінші
жолын алу үшін бірінші жолды
![]() ге
көбейтіп, үшінші жолға қостық. Жүйе
матрицасы үшбұрышты түрге келді. Енді
қайтадан матрицадан жүйеге көшейік
және соңғы жолдан бастап жазайық.
ге
көбейтіп, үшінші жолға қостық. Жүйе
матрицасы үшбұрышты түрге келді. Енді
қайтадан матрицадан жүйеге көшейік
және соңғы жолдан бастап жазайық.
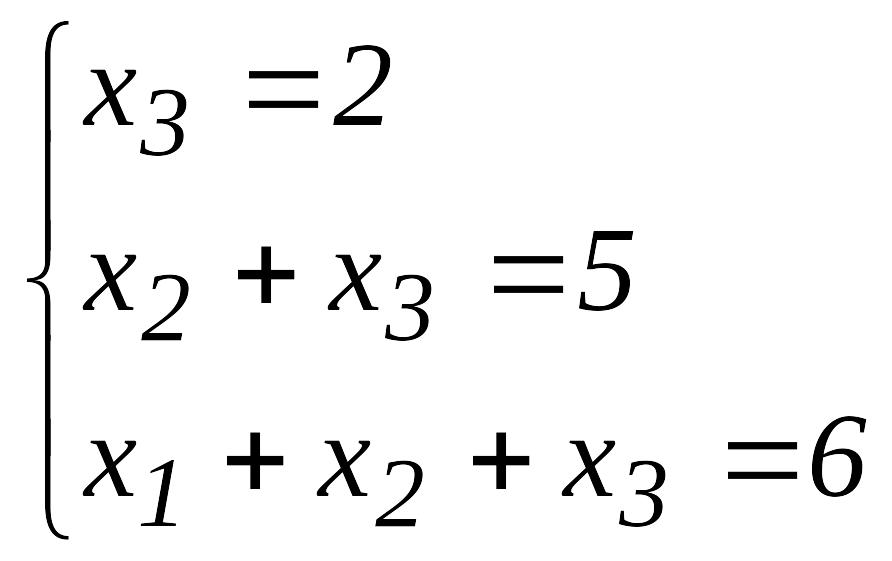 .
Осыдан
.
Осыдан
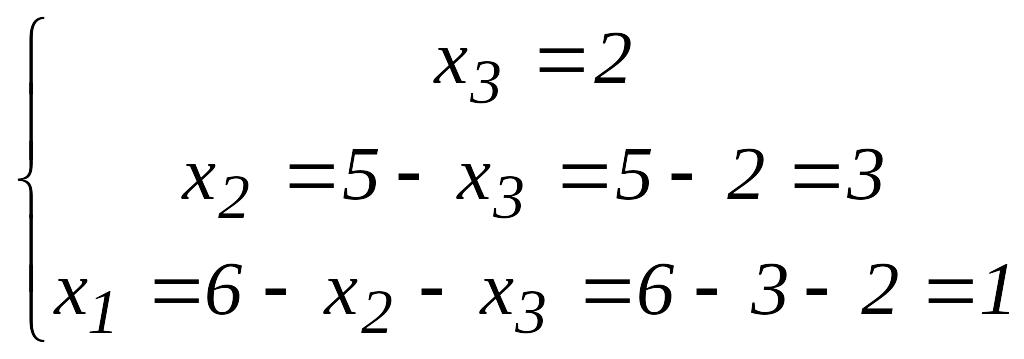 .
Жауабы:
.
Жауабы:
![]()
Теорема
(Кронекер-Капелли)
жүйе үйлесімді болуы үшін жүйенің
матрицасының рангі кеңейтілген матрицаның
рангіне тең болуы қажетті және жеткілікіті,
яғни
![]() .
.
Әдебиеттер: 1 нег.[ 20-41], 11 қос. [115-135].
Бақылау сұрақтар:
1. Матрицаның рангісінің анықтамасын беріңіз.
2. Кері матрицаның анықтамасын беріңіз.
3. Кері матрица қалай есептелінеді?
4. Сызықтық теңдеулер жүйесін шешудің әдістерін айтыңыз.
№3-дәріс. Векторлар. Скалярлық көбейтінді. Векторлар
Вектор
деп бағытталған
кесіндіні айтады, яғни кесіндінің
белгілі бір ұзындығы және бағыты болады.
Егер А
– вектордың басы, ал В
–вектордың ұшы болса, онда вектор
![]() немесе
немесе
![]() символымен белгіленеді.
символымен белгіленеді.
![]() векторы
векторына
қарама-қарсы
вектор
деп аталады (оның басы В
нүктесінде, ал ұшы А
нүктесінде орналасқан).
векторына қарама-қарсы векторды
векторы
векторына
қарама-қарсы
вектор
деп аталады (оның басы В
нүктесінде, ал ұшы А
нүктесінде орналасқан).
векторына қарама-қарсы векторды
![]() деп белгілейді.
векторының ұзындығы
немесе модулі
деп
кесіндісінің ұзындығын айтады және оны
деп белгілейді.
векторының ұзындығы
немесе модулі
деп
кесіндісінің ұзындығын айтады және оны
![]() немесе
немесе
![]() деп белгілейді. Ұзындығы нөлге тең
векторды нөлдік вектор
деп атайды және ол
деп белгілейді. Ұзындығы нөлге тең
векторды нөлдік вектор
деп атайды және ол
![]() деп белгіленеді. Нөлдік вектордың бағыты
болмайды.
деп белгіленеді. Нөлдік вектордың бағыты
болмайды.
Ұзындығы
бірге тең векторды бірлік
вектор деп атайды
және оны
![]() деп белгілейді. Егер бірлік вектордың
бағыты
векторының бағытымен сәйкес келсе, онда
ол
векторының орты
деп аталады және
деп белгілейді. Егер бірлік вектордың
бағыты
векторының бағытымен сәйкес келсе, онда
ол
векторының орты
деп аталады және
![]() деп белгіленеді.
деп белгіленеді.
Параллель
түзулерде немесе бір түзудің бойында
жататын векторлар коллинеар
векторлар деп аталады
және
||![]() деп белгіленеді. Коллинеар векторлар
бағыттас болуы да, қарама-қарсы
бағытта да болуы мүмкін.
деп белгіленеді. Коллинеар векторлар
бағыттас болуы да, қарама-қарсы
бағытта да болуы мүмкін.
Егер
екі
және
векторлары коллинеар болып, бағыттас
және ұзындықтары бірдей болса, онда
оларды тең векторлар
(![]() )
дейді. Тең векторлар еркін векторлар
деп те аталады. Бұл векторлардың басталған
нүктесін кеңістіктегі кез келген нүктеге
көшіруге болады. Аналитикалық геометрияда
еркін (бос) векторлар қарастырылады.
)
дейді. Тең векторлар еркін векторлар
деп те аталады. Бұл векторлардың басталған
нүктесін кеңістіктегі кез келген нүктеге
көшіруге болады. Аналитикалық геометрияда
еркін (бос) векторлар қарастырылады.
Егер кеңістіктегі үш вектор бір жазықтықта немесе параллель жазықтықтарда жатса, онда олар компланар векторлар деп аталады.
Векторларға қолданылатын сызықтық амалдар
Сызықтық амалдар деп, векторларды қосу және алу, векторды санға көбейту амалдарын айтады.
Екі вектордың қосындысын екі жолмен табуға болады: бірі параллелограмм әдісі, екіншісі үшбұрыштар әдісі.
Параллелограмм
әдісі.
және
векторларының қосындысы
![]() деп,
және
векторларының ортақ бас нүктесінен
шығатын, параллелограммның диагоналіне
сәйкес келетін векторды айтады.
деп,
және
векторларының ортақ бас нүктесінен
шығатын, параллелограммның диагоналіне
сәйкес келетін векторды айтады.
Үшбұрыштар әдісі. Егер векторының басы векторының ұшына орналасса, онда және векторларының қосындысы деп, векторының басы мен векторының ұшын қосатын векторды айтады.
Бір
нүктеден шығатын
және
векторларының айырымы
![]() деп
векторының ұшын
векторының ұшымен қосатын векторды
айтады.
деп
векторының ұшын
векторының ұшымен қосатын векторды
айтады.
векторының
санына
көбейтіндісі деп ұзындығы
![]() -ға
тең,
векторына коллинеар, егер
-ға
тең,
векторына коллинеар, егер![]() болса
векторымен бағыттас және
болса
векторымен бағыттас және
![]() болса,
векторына қарама-қарсы бағытталған
болса,
векторына қарама-қарсы бағытталған
![]() векторын айтады.
және
векторларының коллинеарлығының
қажетті және жеткілікті шарты:
векторын айтады.
және
векторларының коллинеарлығының
қажетті және жеткілікті шарты:
![]()
![]()
Векторлардың сызықтық тәуелділігі. Базис
![]() векторлар
жүйесі берілсін.
векторлар
жүйесі берілсін.
векторлар жүйесі үшін бәрі бірдей нөлге тең емес және
![]()
![]()
теңдігін
қанағаттандыратын
![]() сандары табылса, онда
векторларын сызықтық
тәуелді векторлар
деп атайды. Ал егер
теңдік тек
сандарының барлығы бірдей нөлге тең
болғанда ғана орындалса, онда
векторлар жүйесі сызықтық
тәуелсіз деп аталады.
сандары табылса, онда
векторларын сызықтық
тәуелді векторлар
деп атайды. Ал егер
теңдік тек
сандарының барлығы бірдей нөлге тең
болғанда ғана орындалса, онда
векторлар жүйесі сызықтық
тәуелсіз деп аталады.
Егер
![]() теңдігі орындалатын
сандары
табылса, онда
теңдігі орындалатын
сандары
табылса, онда
![]() векторы
векторларының сызықтық
комбинациясы деп
аталады.
векторы
векторларының сызықтық
комбинациясы деп
аталады.
Теорема. Екі вектор сызықтық тәуелді болуы үшін олардың өзара коллинеар болуы қажетті және жеткілікті.
Бұл теоремадан кез келген коллинеар емес екі вектор сызықтық тәуелсіз болады деген қорытынды шығады.
Теорема.
Үш вектор сызықтық
тәуелді болуы үшін олардың компланар
болуы қажетті және жеткілікті. Бұл
теоремадан кез келген компланар емес
үш вектор сызықтық
тәуелсіз векторлар
жүйесін құрайды деген қорытынды шығады.
Егер жазықтықта кез келген
векторы үшін
![]() нақты сандары табылып, мына теңдік
нақты сандары табылып, мына теңдік
![]() орындалса, онда белгілі ретпен алынған
орындалса, онда белгілі ретпен алынған
![]() сызықтық тәуелсіз векторлар жұбы
жазықтықтағы базис
деп аталады. Мұндағы
сандары
векторының
базисіндегі координаттары деп аталады
да былай белгіленеді:
сызықтық тәуелсіз векторлар жұбы
жазықтықтағы базис
деп аталады. Мұндағы
сандары
векторының
базисіндегі координаттары деп аталады
да былай белгіленеді:
![]() .
Егер кеңістікте кез келген
векторы үшін
.
Егер кеңістікте кез келген
векторы үшін
![]() нақты сандары табылып, мына теңдік
нақты сандары табылып, мына теңдік
![]() орындалса, онда белгілі ретпен алынған
сызықтық тәуелсіз
орындалса, онда белгілі ретпен алынған
сызықтық тәуелсіз
![]() векторлар үштігін кеңістіктегі
базис деп атайды.
Мұндағы
сандары
векторының
базисіндегі координаттары деп аталады
да былай белгіленеді:
векторлар үштігін кеңістіктегі
базис деп атайды.
Мұндағы
сандары
векторының
базисіндегі координаттары деп аталады
да былай белгіленеді:
![]() .
.
Базисті құраушы векторлар базистік векторлар деп аталады. Осы анықтамалар мен теоремалардан кез келген коллинеар емес екі вектор жазықтықта, ал кез келген компланар емес үш вектор кеңістікте базистік векторлар жүйесі болады деген қорытынды шығады.
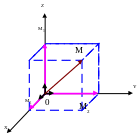
Векторды
координат өстердің орттары арқылы
жіктеу. Вектордың модулі. Кеңістіктегі
тік бұрышты декарттық
![]() координаталар жүйесін қарастырайық.
Ох, Оу, Oz координат
өстерінің бойында жатқан бірлік (орт)
векторларды сәйкесінше
координаталар жүйесін қарастырайық.
Ох, Оу, Oz координат
өстерінің бойында жатқан бірлік (орт)
векторларды сәйкесінше
![]() деп белгілейік. Сонда реттелген үштік
кеңістікте базистік векторлар жүйесін
құрайды. Мұндай, базистік векторлар
жүйесін ортогональ базистік жүйе (базис)
деп атайды
деп белгілейік. Сонда реттелген үштік
кеңістікте базистік векторлар жүйесін
құрайды. Мұндай, базистік векторлар
жүйесін ортогональ базистік жүйе (базис)
деп атайды
![]() .
.
![]()
![]() ,
себебі үш вектордың қосындысы.
,
себебі үш вектордың қосындысы.
Бұл
формула
![]() вектордың координат
өстерінің орттары арқылы жіктелген
түрі деп аталады немесе қысқаша
вектордың координат
өстерінің орттары арқылы жіктелген
түрі деп аталады немесе қысқаша
![]() деп жазады.
деп жазады.
Екінші
жағынан
![]() =
=![]() ,
Осыдан
,
Осыдан
![]() болғандықтан
болғандықтан
![]() -
вектордың модулі
(ұзындығы).
-
вектордың модулі
(ұзындығы).
1-мысал.
Егер
![]() ,
онда
,
онда
![]() Егер
векторы Ох, Оу, Oz өстерімен
сәйкесінше
Егер
векторы Ох, Оу, Oz өстерімен
сәйкесінше
![]() бұрыштарын құрса, онда
бұрыштарын құрса, онда
![]() ,
осыдан
,
осыдан
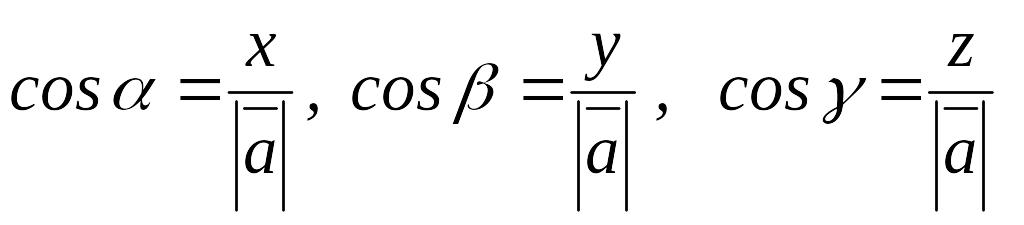 болады.
болады.
Мұндағы
![]() сандары
векторының бағыттаушы
косинустары деп
аталады. Алдыңғы өрнекті вектордың
модулінің формуласына қойып,
сандары
векторының бағыттаушы
косинустары деп
аталады. Алдыңғы өрнекті вектордың
модулінің формуласына қойып,
![]() теңдігін
аламыз.
бірлік векторының коодинаттары
екенін оңай байқауға
болады . Сонымен,
теңдігін
аламыз.
бірлік векторының коодинаттары
екенін оңай байқауға
болады . Сонымен,
![]() .
.
2-мысал.
![]() векторы үшін
векторы үшін
![]()
Координаттарымен берілген векторларға амалдар қолдану
![]() ,
,
![]() болса,
болса,
![]()
![]()
Векторлардың теңдігі
![]() болғанда
ғана
және
векторлары тең болады, яғни
болғанда
ғана
және
векторлары тең болады, яғни
![]()
Векторлардың
коллинеарлығы.
||
болғандықтан оны
деп жазуға болады,
мұндағы
-
қайсыбір сан. Осыдан
![]()
![]()
![]() -екі вектордың
коллинеарлығының белгісі.
-екі вектордың
коллинеарлығының белгісі.
Нүктенің
координатасы. Кеңістікте
тік бұрышты декарттық
координаттар жүйесі берілсін. Кез
келген М нүктесінің
координаты деп,
![]() векторының координатын айтады.
векторы М нүктесінің
радиус-векторы деп аталады және
векторының координатын айтады.
векторы М нүктесінің
радиус-векторы деп аталады және
![]() деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,
![]() немесе
немесе
![]() .
М нүктесінің
координатасы
.
М нүктесінің
координатасы
![]() деп жазылады.
деп жазылады.
Вектордың
координатасы. Егер
![]() және
және
![]() нүктелерінің координаттары берілсе,
онда
нүктелерінің координаттары берілсе,
онда
![]() векторының координатасы
былай есептелінеді:
векторының координатасы
былай есептелінеді:
![]() .
.
3-мысал.
![]() берілсе, онда
берілсе, онда
![]() базисінде
базисінде
![]()
![]() .
.
Кесіндіні
берілген қатынаста бөлу.
және
нүктелері арқылы өтетін кесінді берілсін.
Осы кесіндіні
қатынасындай етіп бөлетін
![]() нүктесінің координаттары:
нүктесінің координаттары:
![]() ,
,
![]() ,
,
![]() - кесіндіні берілген
қатынаста бөлу формулаларымен анықталады.
Егер
- кесіндіні берілген
қатынаста бөлу формулаларымен анықталады.
Егер
![]() болса, яғни
болса, яғни
![]() онда
онда
![]() ,
,
![]() ,
,
![]() - кесіндінің ортасын
табу формуласы.
- кесіндінің ортасын
табу формуласы.
Векторлардың скалярлық көбейтіндісі
Анықтама.
Екі
![]() және
және
![]() векторларының
скалярлық көбейтіндісі
деп
векторларының
скалярлық көбейтіндісі
деп
![]() санын айтады. Скаляр көбейтінді
санын айтады. Скаляр көбейтінді
![]() ,
,
![]() ,
,
![]() символдармен белгіленеді. Мұндағы
символдармен белгіленеді. Мұндағы
![]()
![]() (
),
болғандықтан
(
),
болғандықтан
![]() деп жазуға болады.
деп жазуға болады.
4-мысал.
Егер
![]() ,
,
![]() ,
,
![]() ,
онда
,
онда
![]()
Теорема.
базисінде
векторының координаталары
![]() ,
ал
векторының координаталары
,
ал
векторының координаталары
![]() болсын. Онда
болсын. Онда
![]() .
.
5-мысал.
Егер
,
![]() болса, онда
болса, онда
![]()
Скалярлық көбейтіндінің қолданылуы
1.
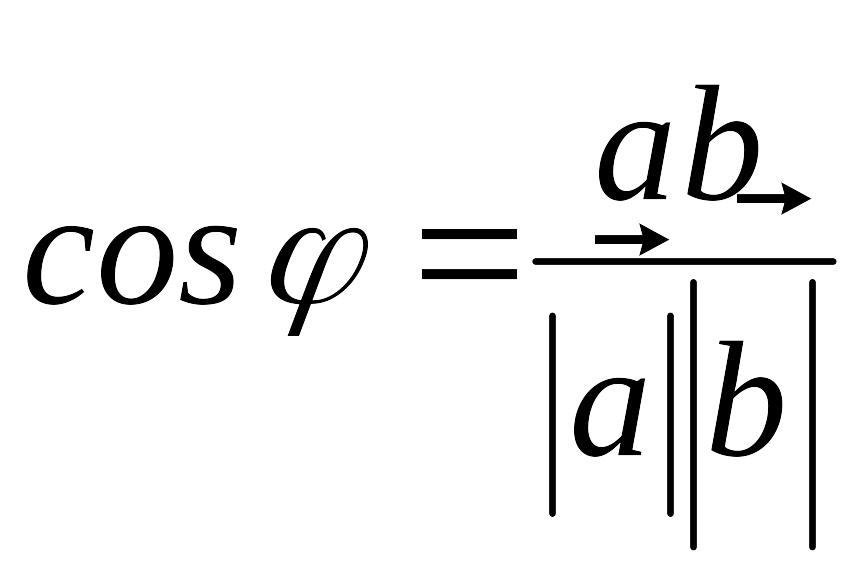 немесе
немесе
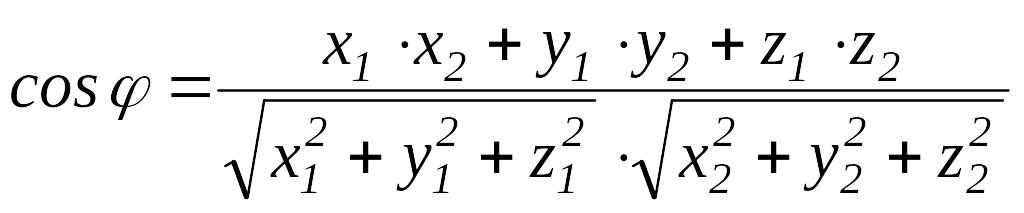
2.
![]()
![]()
![]()
3.
 (
(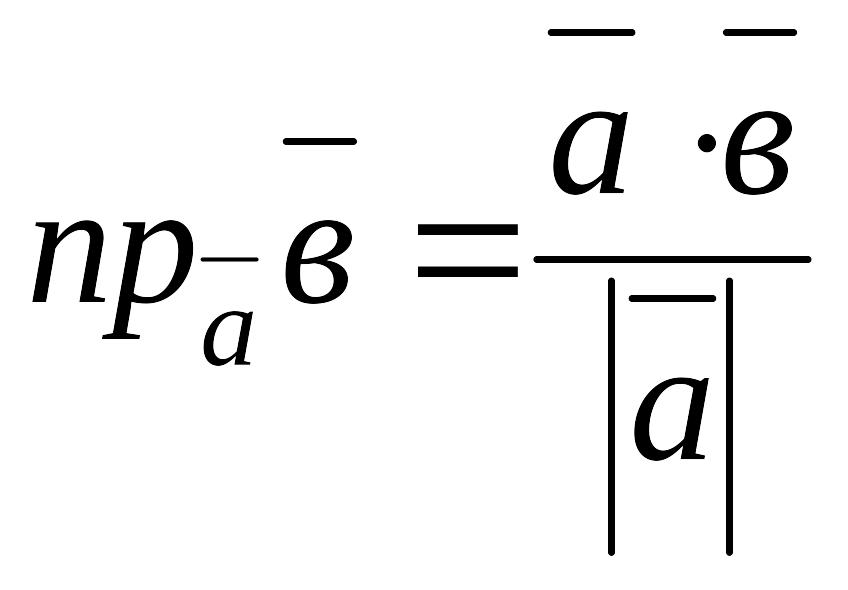 )
немесе
)
немесе
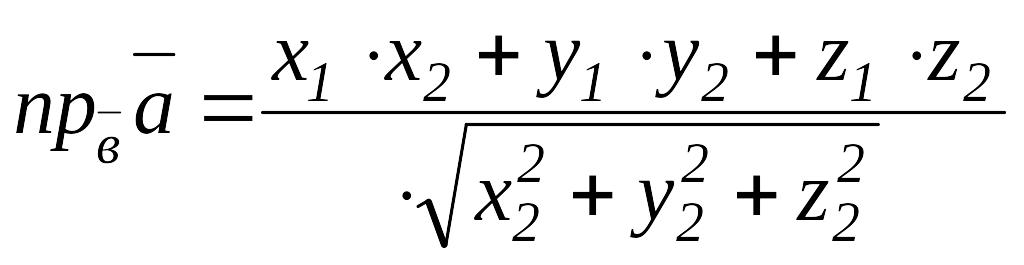
Әдебиеттер: 1 нег. [45-65 беттер, 11 қос. [136-156].
Бақылау сұрақтар:
1. Вектор деген не? Векторларға қандай амалдар қолданылады?
2. Вектордың үзындығын қай формуламен есептейді?
3. Кесіндінің қақ ортасын табу формуласын көрсетіңіз.
4. Скаляр көбейтіндінің анықтамасын беріңіз.
5. Скаляр көбейтіндінің механикалық мағынасын түсіндіріңіз.
№4-дәріс. Векторлық және аралас көбейтінділер. Векторлардың векторлық көбейтіндісі
Үш
компланар емес
![]() векторлары берілсін. Егер
векторлары берілсін. Егер
![]() векторының ұшынан қарағанда
векторының ұшынан қарағанда
![]() дан
дан
![]() ға
дейінгі ең қысқа бұрылыс сағат тіліне
қарсы бағытта орындалса, онда
векторлары оң үштік,
ал
дан
ға
дейінгі ең қысқа бұрылыс сағат тілімен
бағыттас болса, онда
сол үштік
құрайды дейді.
ға
дейінгі ең қысқа бұрылыс сағат тіліне
қарсы бағытта орындалса, онда
векторлары оң үштік,
ал
дан
ға
дейінгі ең қысқа бұрылыс сағат тілімен
бағыттас болса, онда
сол үштік
құрайды дейді.
Анықтама.
және
векторларының векторлық
көбейтіндісі деп,
келесі үш шартты қанағаттандыратын
![]() векторын
айтады:
векторын
айтады:
1)
![]() ;
;
2)
![]() векторының
ұзындығы
және
векторларына тұрғызылған параллелограммның
ауданына тең, яғни
векторының
ұзындығы
және
векторларына тұрғызылған параллелограммның
ауданына тең, яғни
![]() ,
мұндағы
;
,
мұндағы
;
3) векторлары оң үштік құрайды.
Векторлық
көбейтінді
![]() немесе
немесе
![]() деп белгіленеді.
деп белгіленеді.
Векторлық
көбейтіндінің анықтамасынан
![]() ,
,
![]() ,
,
![]() болады
болады
Векторлық көбейтіндінің қасиеттері:
1.
![]() ;
;
2.
![]() ;
;
3.
Нөлдік емес
және
векторлары
![]() жағдайда ғана колинеар;
жағдайда ғана колинеар;
4.
![]() .
.
Теорема.
Егер
![]() базисінде
базисінде
![]()
![]() векторлары берілсе, онда
векторлары берілсе, онда
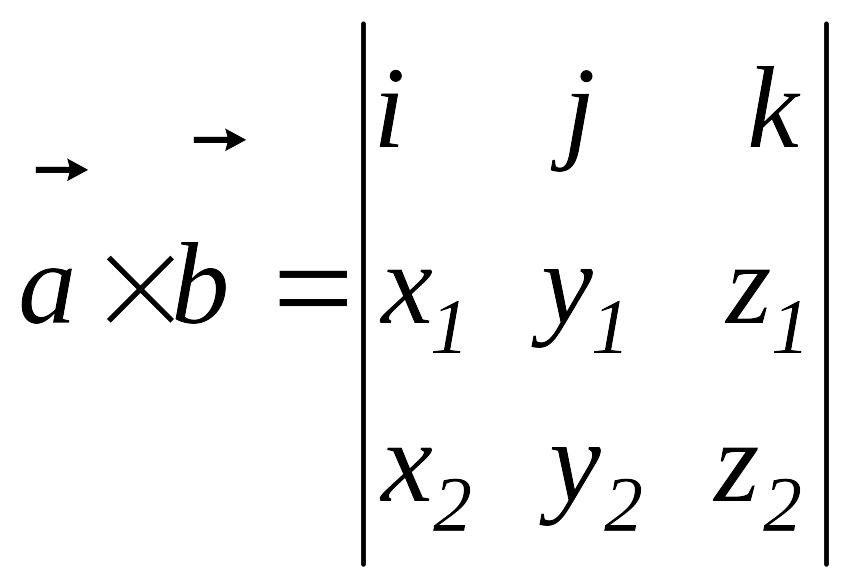
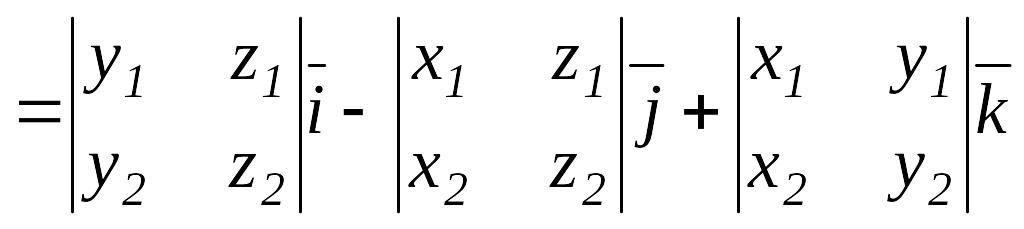 .
.
1-мысал.
![]()
![]() векторларының векторлық көбейтіндісін
табу керек.
векторларының векторлық көбейтіндісін
табу керек.
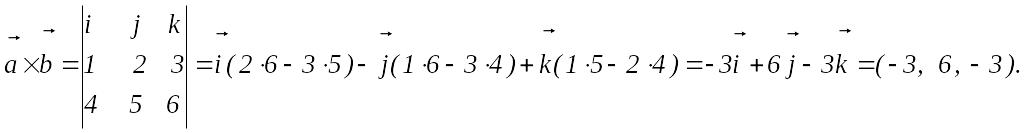 Векторлық
көбейтіндінің қолданылуы
Векторлық
көбейтіндінің қолданылуы
1.
![]() ,
,
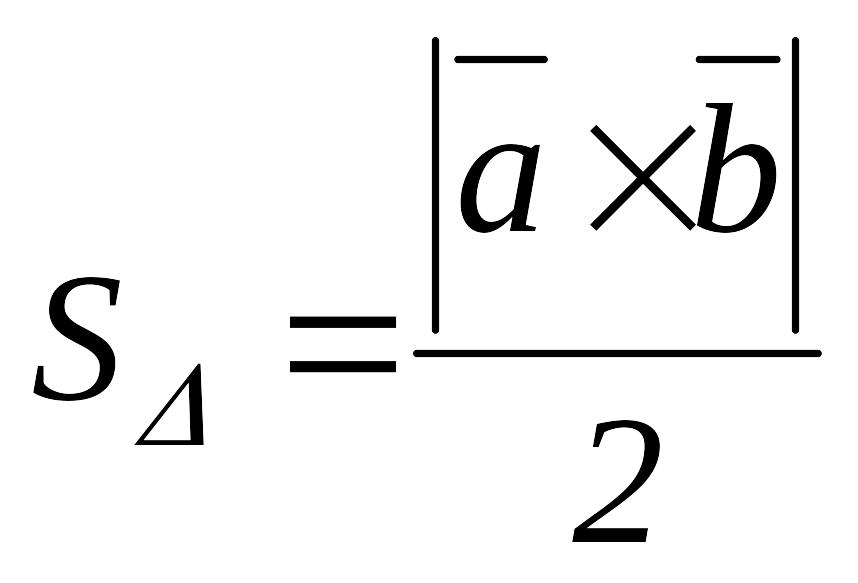
2.
Егер
||
болса, онда
![]() (және
керісінше)
(және
керісінше)
Векторлардың аралас көбейтіндісі
Анықтама.
векторларының аралас көбейтіндісі деп,
және
векторларының векторлық көбейтіндісі
мен
векторының
скаляр көбейтіндісін айтады.![]()
Аралас
көбейтінді
![]() не
не
![]() немесе
немесе
![]() түрінде жазылады. Аралас көбейтіндінің
нәтижесі санға тең.
түрінде жазылады. Аралас көбейтіндінің
нәтижесі санға тең.
Аралас көбейтіндінің қасиеттері:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
Егер векторлар
компланар болса, онда
![]() .
.
Теорема.
базисінде
![]() ,
,
,
,
![]() векторлары берілсін, онда олардың аралас
көбейтіндіні анықтауыш түрінде жазуға
болады.
векторлары берілсін, онда олардың аралас
көбейтіндіні анықтауыш түрінде жазуға
болады.
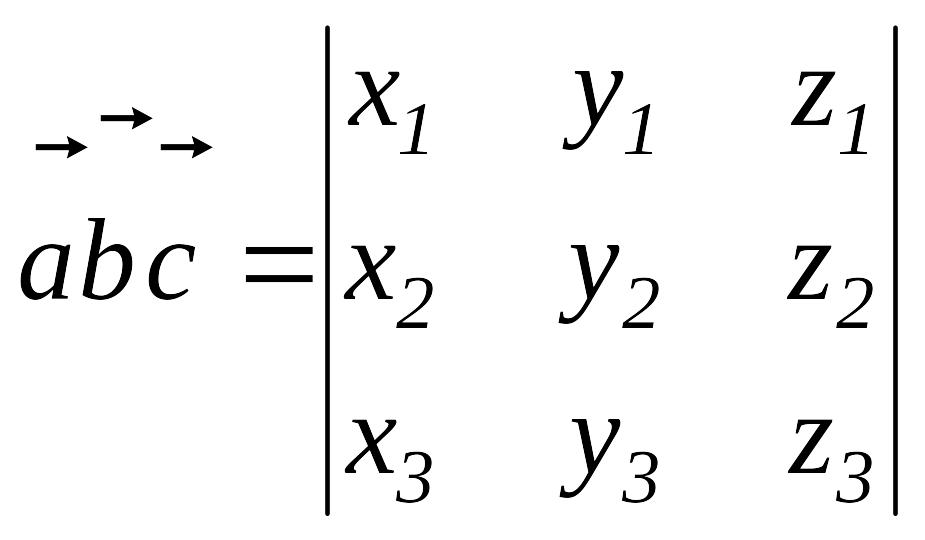
Аралас көбейтіндінің қолданылуы
Егер
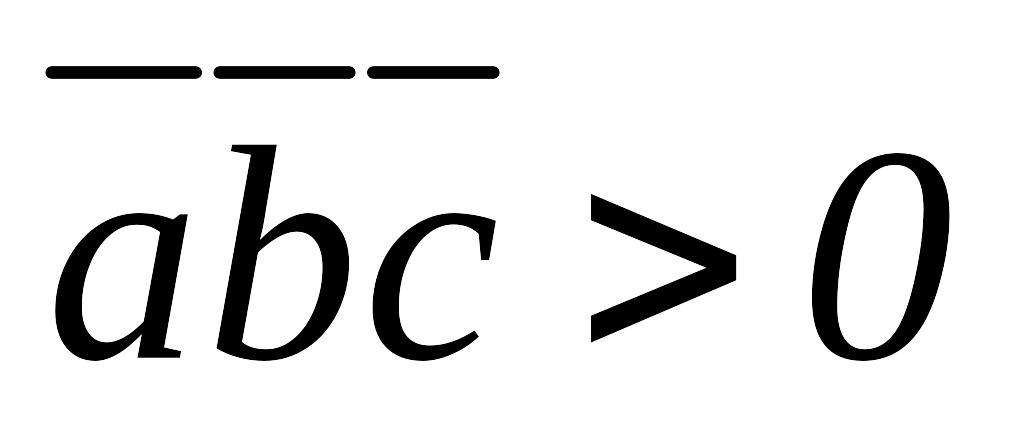 болса, онда
-оң үштік; егер
болса, онда
-оң үштік; егер
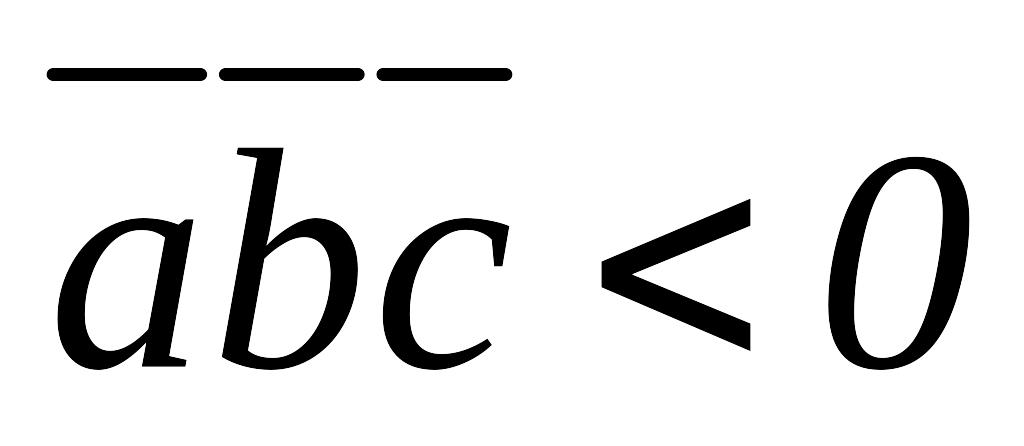 болса, онда
- сол үштік құрайды.
болса, онда
- сол үштік құрайды.
векторлары компланар.
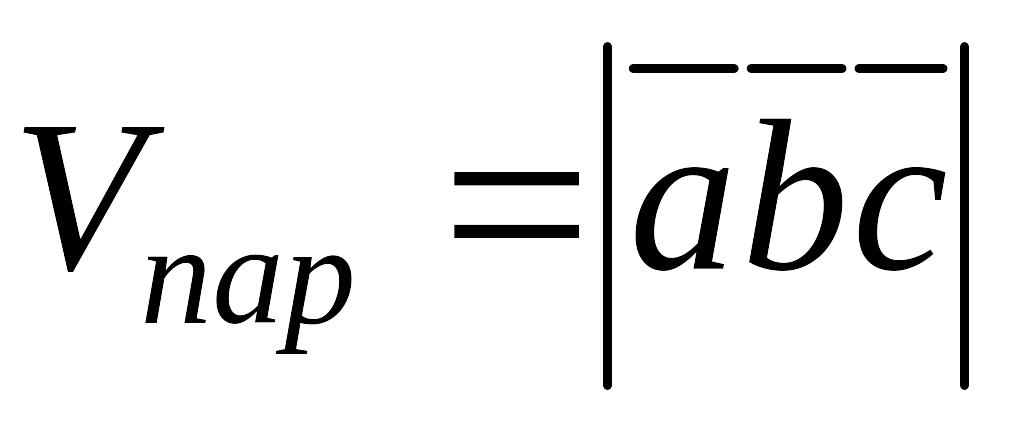 ,
,
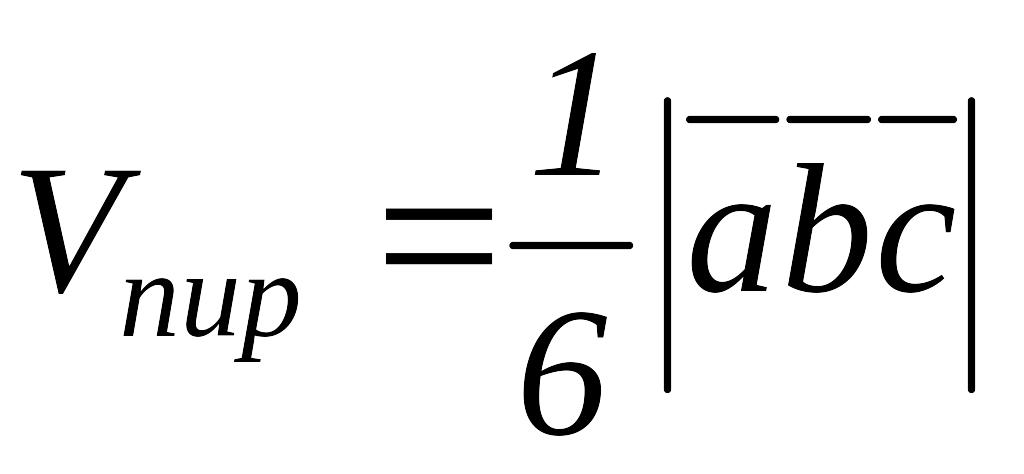 .
.
Жазықтықтағы түзудің теңдеулері
