Расчет надежности комбинированных систем

Для расчета надежности комбинированных систем целесообразно предварительно произвести декомпозицию системы, разбив ее на простые подсистемы – группы элементов, методика расчета надежности которых известна. Затем эти подсистемы в структурной схеме надежности заменяются элементами (квазиэлементами) с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем. При необходимости такую процедуру можно выполнить несколько раз, до тех пор, пока не получится структура, методика расчета надежности которой известна.

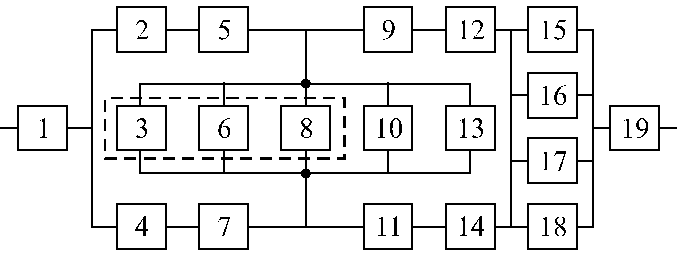
В качестве примера рассмотрим комбинированную систему, представленную на рис. 1.15. Здесь элементы (2 и 5), (4 и 7), (9 и 12), (11 и 14) попарно образуют друг с другом последовательные соединения. Заменим их соответственно элементами А, В, С, D, для которых расчет надежности рассматривался ранее.

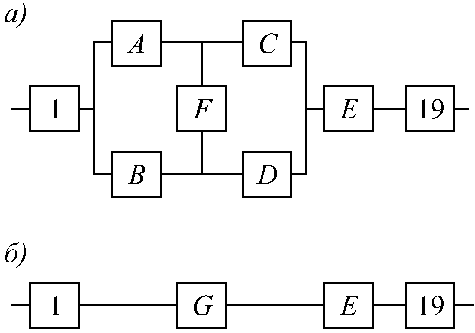
Элементы 15, 16, 17 и 18 образуют параллельное соединение, а элементы 3, 6, 8, 10 и 13 – систему “3 из 5”. Соответствующие элементы обозначим E и F. В результате преобразованная схема примет вид, показанный на рис. 1.16, а. В ней в свою очередь элементы А, В, С, D, F образуют мостиковую схему, которую заменяем элементом G.

Рис. 1.15. Исходная система	Рис. 1.16. .Преобразованные системы

После таких преобразований получается последовательная система, состоящая из элементов 1, G, E, 19 (рис. 1.16, б).

Порядок выполнения работы

1. Обучающиеся совместно с преподавателем решают пример по условиям задачи 1.

Задача 1

Условие. Двигатель легкового автомобиля имеет 4 свечи зажигания, по одной на каждый цилиндр. Интенсивность отказов свечи  = 10^-3 1/ч, а длительность работы двигателя в течение всего маршрута t = 20 ч. Предполагается, что автомобиль может ехать также при одном неработающем цилиндре. Какова вероятность того, что автомобиль доставит пассажиров в пункт назначения без замены свечей

Решение. Благоприятные ситуации, не приводящие к отказу двигателя в целом возникают в том случае, если:

1. А – за время t ни одна из свечей не отказала;

2. Б – отказала одна свеча, проработав время   t, при этом 3 остальные остались исправными в течение времени t.

3. Вероятность того, что не откажет ни одна свеча будет равна произведению вероятностей p(t) безотказной работы всех четырех свечей, т.е. P_А(t) = p⁴(t).

4. Вероятность того, что три свечи исправны, а одна нет, равна p³q.

5. Так как в цилиндрах четыре свечи, то возможен выход из строя любой из них, поэтому вероятность гипотезы Б

P_Б(t) = C¹₄ p³(t)q(t) = 4p³(t)(1-p(t)).

6. Коэффициент C¹₄ имеет место, поскольку может отказать любая свеча (одна из четырех).

7. Суммируя вероятности гипотез А и Б, получим

P_С(t) = P_А(t) + P_Б(t) = p⁴(t) + 4p³(t)(1-p(t)) = p³(t)[p(t) + 4(1-p(t)].

8. Имея в виду, что p(t) = exp(-t), то очевидно, что

P_С = exp(-3t)[exp(-t) + 4(1- exp(-t)] =0,996

2. Обучающиеся индивидуально, разрабатывают функциональную модель по условиям задачи 2, считая все устройства отдельными элементами. Преподаватель контролирует и помогает в составлении схем.