Расчет надежности (безотказности) систем с различным соединением элементов

Расчеты показателей безотказности системы обычно проводятся в предположении, что как вся система, так и любой ее элемент могут находиться только в одном из двух возможных состояний – работоспособном или неработоспособном – и отказы элементов независимы друг от друга. Состояние системы (работоспособное или неработоспособное) определяется состоянием элементов и их сочетанием. Поэтому теоретически возможно расчет безотказности любой системы свести к перебору всех возможных комбинаций состояний элементов, определению вероятности каждого из них и сложению вероятностей работоспособных состояний системы. Такой метод – метод прямого перебора – практически универсален и может использоваться при расчете любых систем. Однако при большом количестве элементов системы n такой путь становится нереальным из-за большого объема вычислений (например, при n=10 число возможных состояний системы составляет, 2ⁿ= 1024, при n=20 превышает 10⁶, при n=30 – более 10⁹). Поэтому на практике используют более эффективные и экономичные методы расчета, не связанные с большим объемом вычислений. Возможность применения таких методов связана со структурой системы.

Расчет надежности последовательных систем

В последовательных системах для безотказной работы в течение некоторой наработки t необходимо и достаточно, чтобы каждый из ее n элементов работал безотказно в течение этой наработки. Считая отказы элементов независимыми, вероятность одновременной безотказной работы n элементов определяется по теореме умножения вероятностей: вероятность совместного появления независимых событий равна произведению вероятностей этих событий:

,(1.17)

где P_i(t)– вероятность безотказной работы i- го элемента системы; Q_i(t)– вероятность отказа i-го элемента системы.

Вероятность отказа такой системы

,(1.18)

Здесь и далее обозначение наработки (аргумента t) опускается для сокращения записей формул.

Если система состоит из равнонадёжных элементов (P₁= P₂=...= P_n), то

(1.19)

Из формул (1.17) … (1.19) очевидно, что при равной надежности элементов надежность последовательной системы оказывается тем более низкой, чем больше число элементов. Кроме того, поскольку все сомножители в правой части выражения (1.17) не превышают единицы, вероятность безотказной работы системы при последовательном соединении не может быть выше вероятности безотказной работы самого ненадежного из ее элементов (принцип “хуже худшего”) и из малонадежных элементов нельзя создать высоконадежной системы с последовательным соединением.

Если все элементы системы работают в период нормальной эксплуатации и имеет место простейший поток отказов (см. формула (1.10)), то наработки элементов системы подчиняются экспоненциальному распределению (см. (1.8)) и на основании (1.17) можно записать

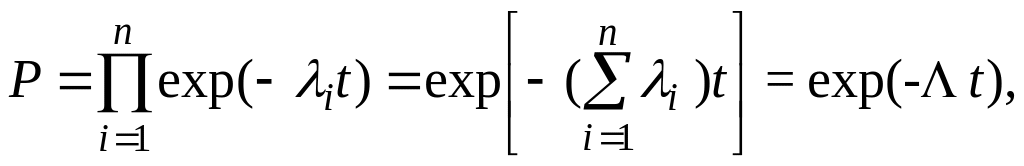(1.20)

где

(1.21)

есть интенсивность отказов системы в целом.

Таким образом, интенсивность отказов системы при последовательном соединении элементов и простейшем потоке отказов равна сумме интенсивностей отказов элементов. С помощью выражений (1.15) и (1.16) могут быть определены средняя и ϒ-процентная наработки.

Из (1.20) – (1.21) следует, что для системы из n равнонадёжных элементов (λ_i=λ)

(1.22)

т.е. интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента.