Приложение 2 Законы распределения непрерывных случайных величин [3, 5, 10]
-
Закон распределения
Дифференциальная функция
Интегральная функция
Математическое ожидание
Дисперсия
Параметры распределения
Нормальный
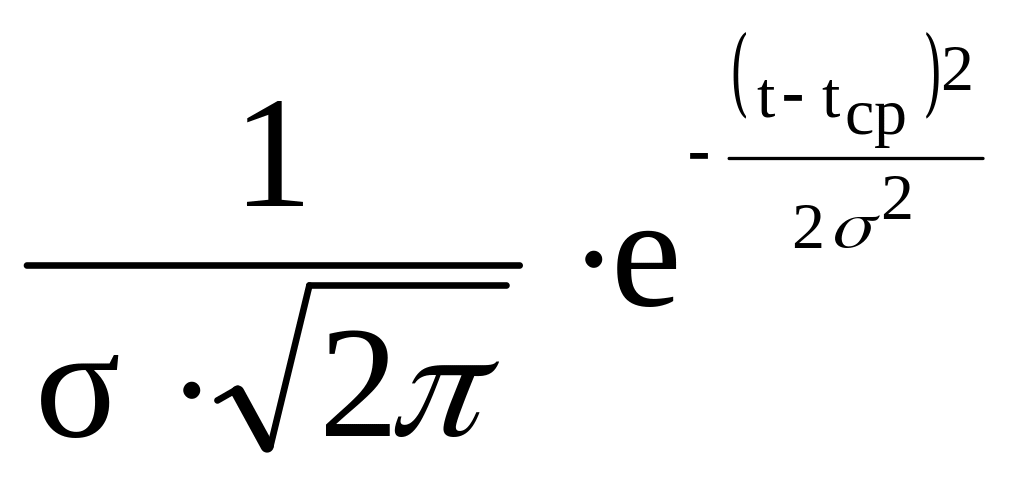
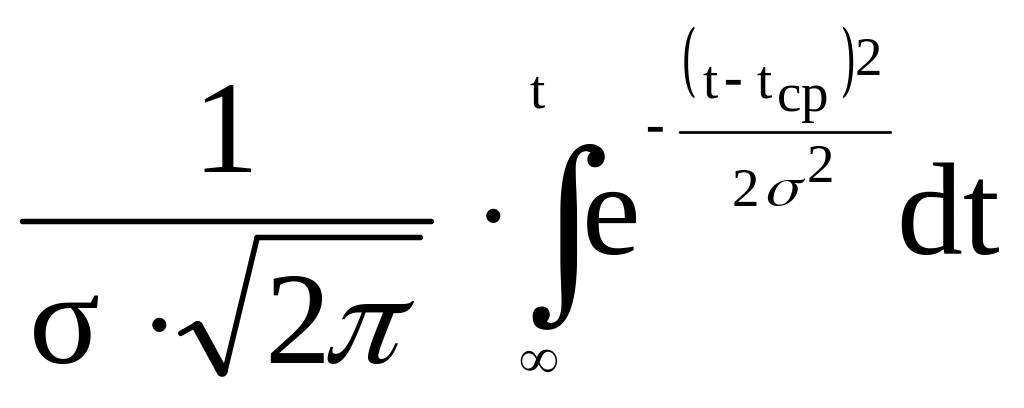
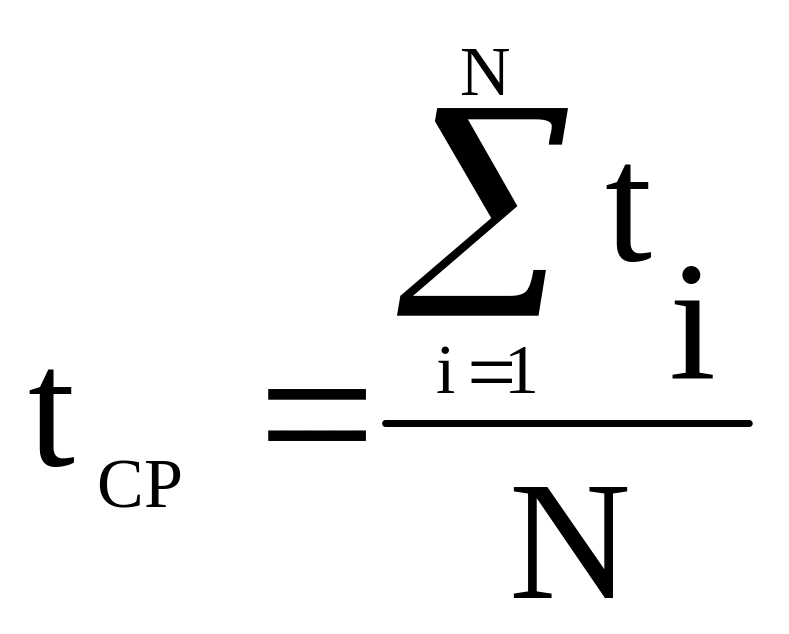
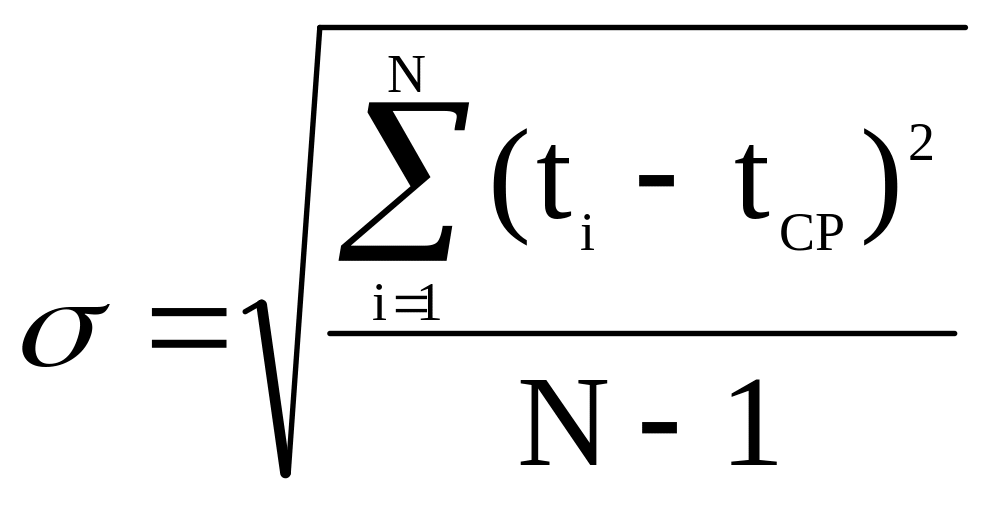
tcp-среднее значение
- среднеквадра-тическое отклонение
tсм=t1-(t3-t1)/2
- величина смещения
Вейбулла
(b/a)(t/a)b-1 [-exp(-t/a)b]
1-exp(-t/a)b
aГ(1+1/b)
aГ(1+2/b)-(Г(1+1/b))2
b- параметр формы
a- масштабный коэффициент
См. приложение.
Гамма-распределение
/
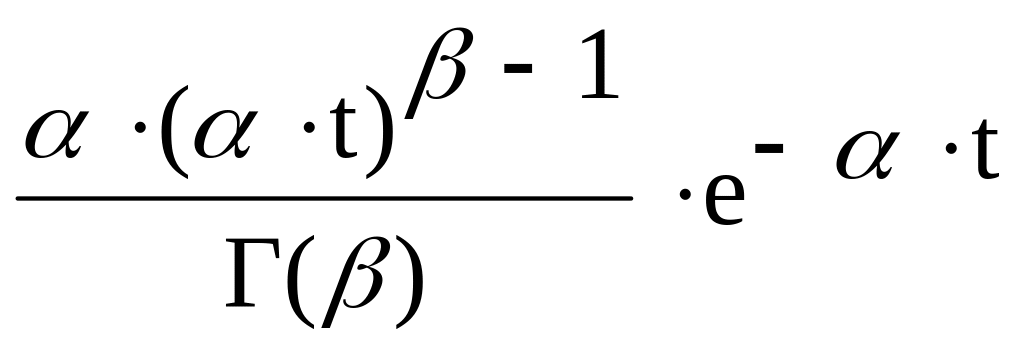
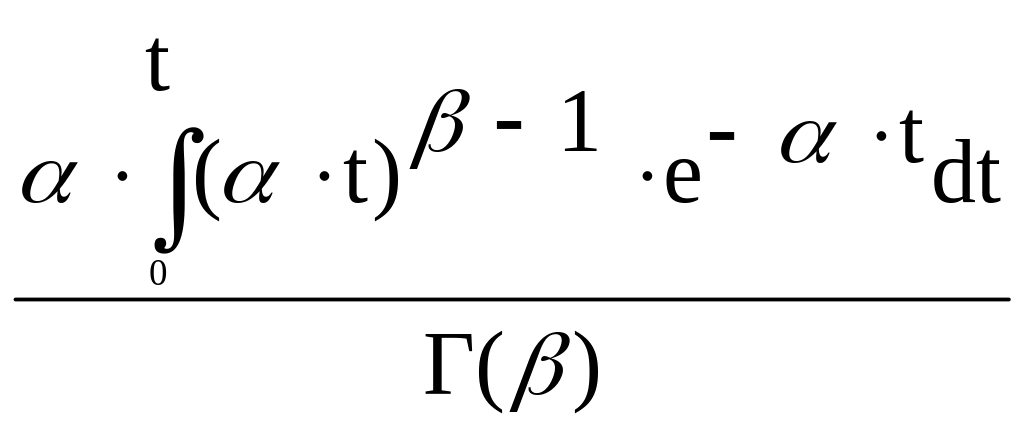
/2
= tcp 2 / 2 -параметр формы
=tcp / 2 - масштабный параметр
Экспоненциальный (показательный)
e-t
1-e-t
1/
1/2
=1/ tcp - параметр распределения
Эрланга
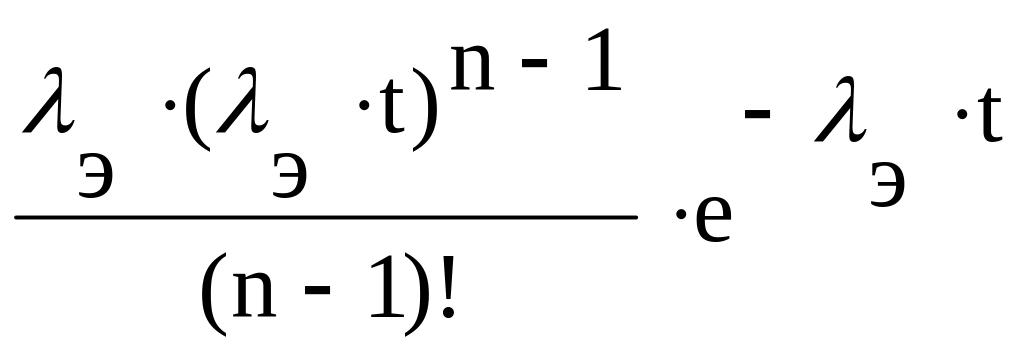
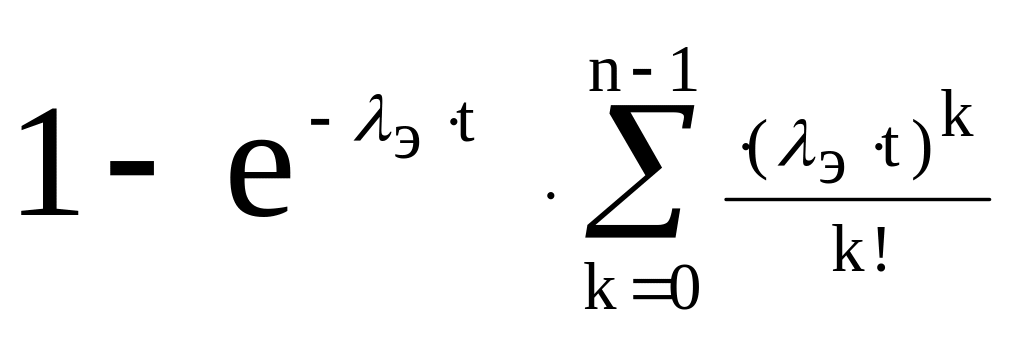
n/э
n/2
э= tcp / 2 - параметр закона Эрланга
n= tcp 2 / 2 - порядок распределения Эрланга (целое число)
Приложение 3
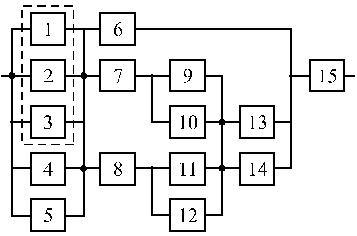
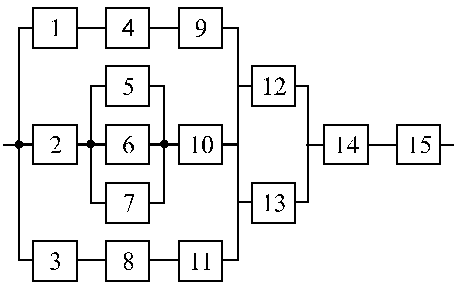
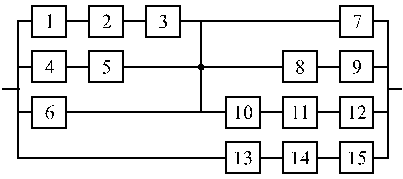
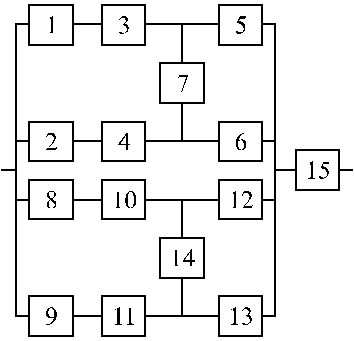
Структурные схемы для расчета безотказности систем
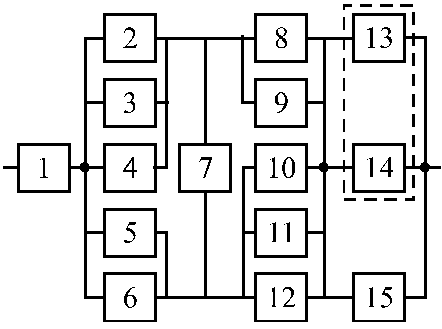
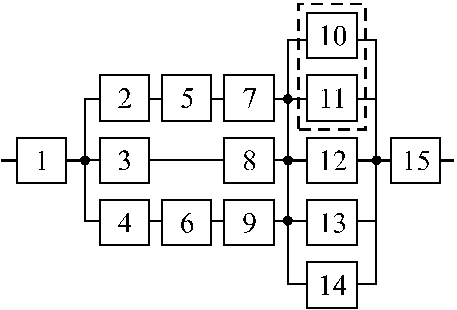
Вариант 1 Вариант 2
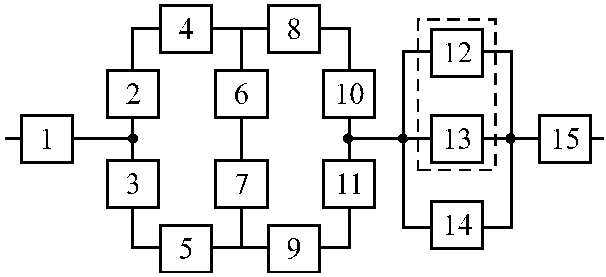
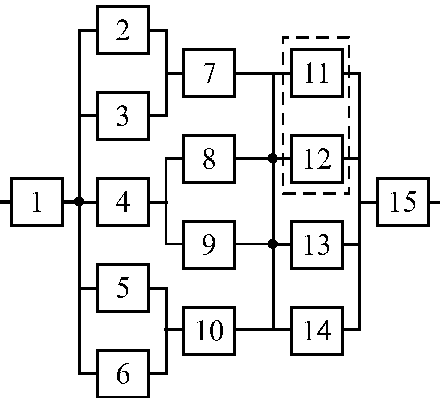
Вариант 3 Вариант 4
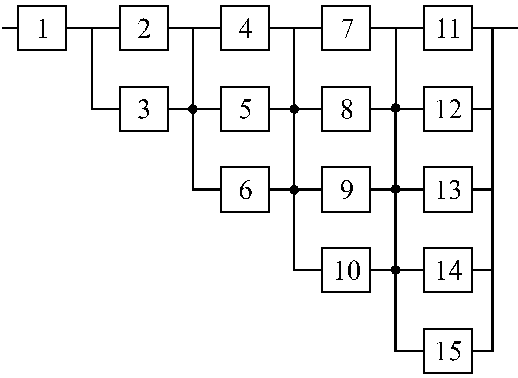
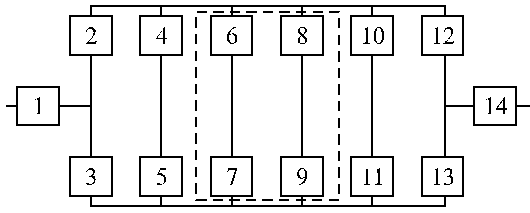
Вариант 5 Вариант 6
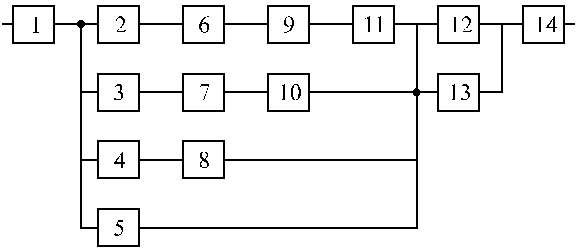
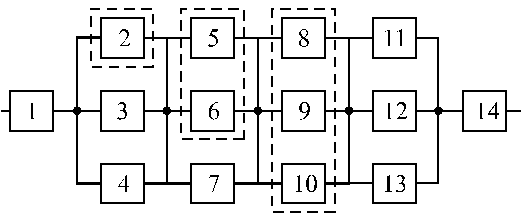
Вариант 7 Вариант 8
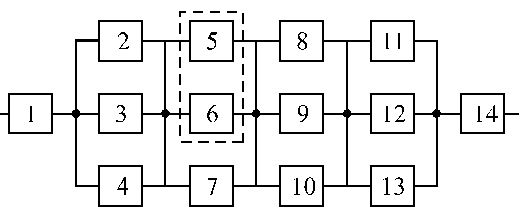
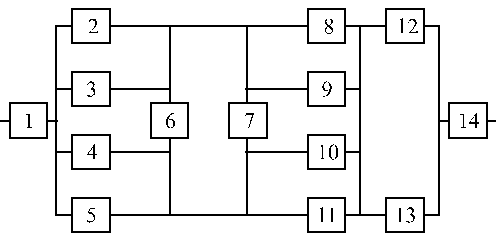
Вариант 9 Вариант 10
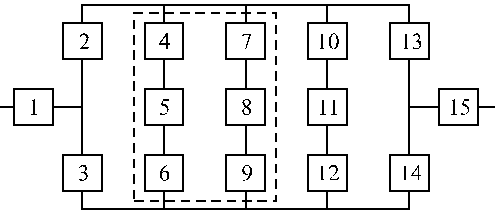
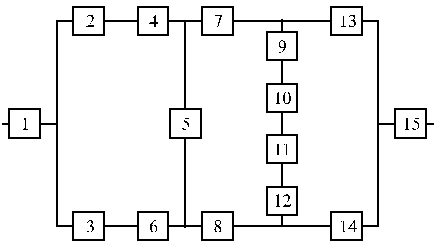
Вариант 11 Вариант 12
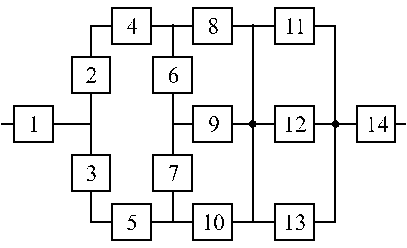
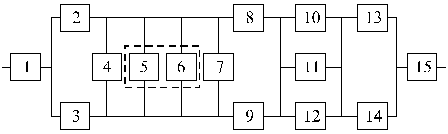
Вариант 13 Вариант 14
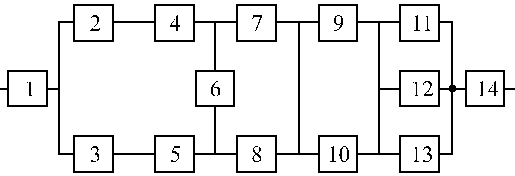
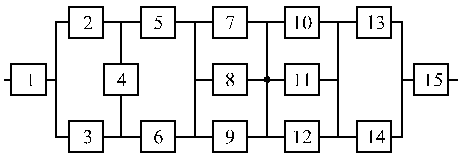
Вариант 15 Вариант 16
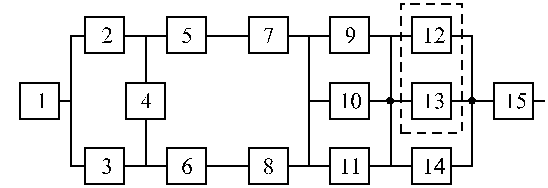
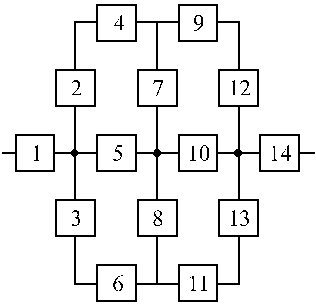
Вариант 17 Вариант 18
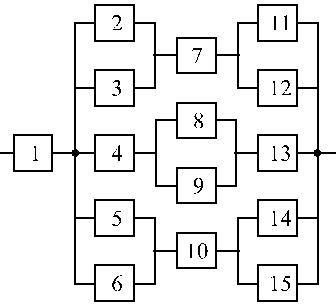
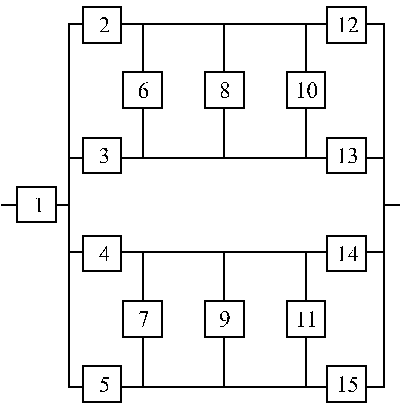
Вариант 19 Вариант 20
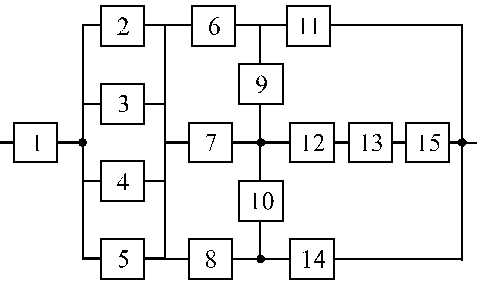
Вариант 21 Вариант 22
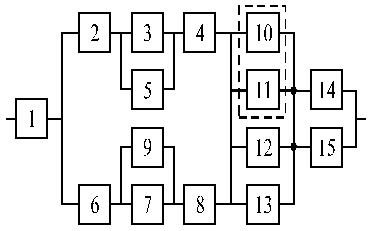
Вариант 23 Вариант 24
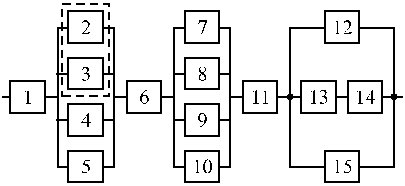
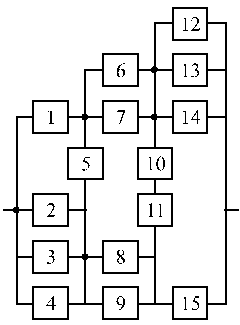
Вариант 25 Вариант 26
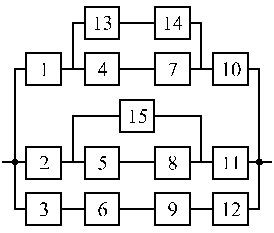
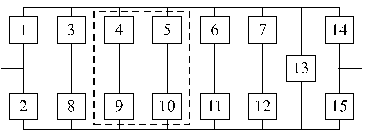
Вариант 27 Вариант 28
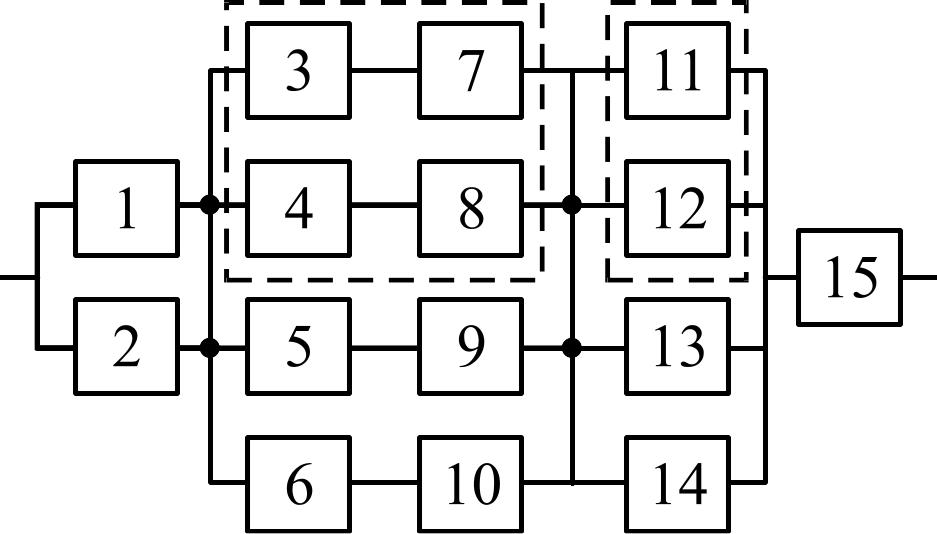
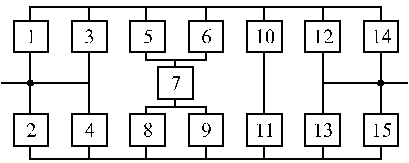
Вариант 29 Вариант 30
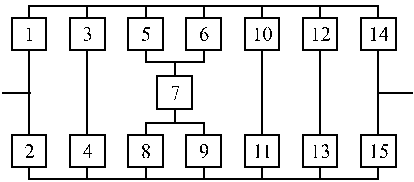
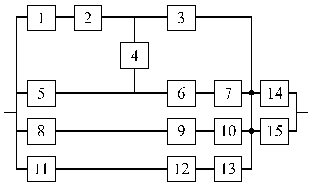
Вариант 31 Вариант 32
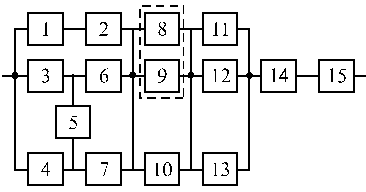
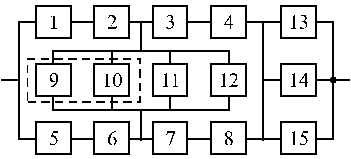
Вариант 33 Вариант 34
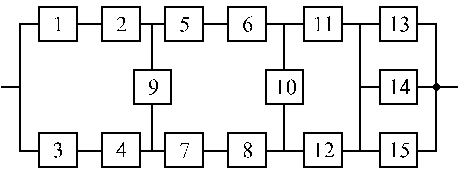
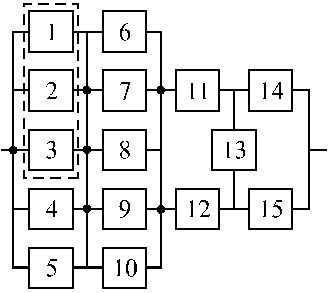
Вариант 35 Вариант 36
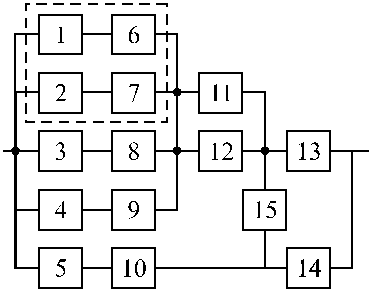
Вариант 37 Вариант 38
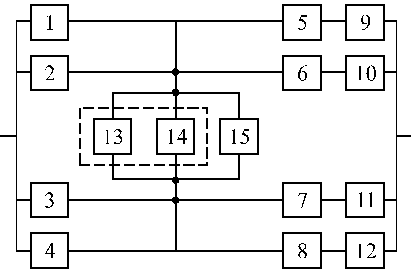
Вариант 39 Вариант 40
Приложение 4
Таблица
Заданные значения показателей надежности
№ |
, |
Интенсивности отказов элементов, i , 10-6 ч-1 |
||||||||||||||
вар. |
% |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
90 |
0,1 |
1 |
1 |
1 |
1 |
1 |
0,5 |
1 |
1 |
1 |
1 |
1 |
0,1 |
0,1 |
0,1 |
2 |
95 |
0,2 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
1 |
1 |
1 |
0,1 |
3 |
80 |
0,1 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
5 |
5 |
5 |
0,2 |
4 |
70 |
0,05 |
1 |
1 |
1 |
1 |
1 |
0,5 |
0,5 |
0,5 |
0,5 |
0,2 |
0,2 |
0,2 |
0,2 |
0,02 |
5 |
50 |
0,01 |
0,05 |
0,05 |
0,1 |
0,1 |
0,1 |
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
1 |
1 |
1 |
6 |
75 |
0,01 |
0,05 |
0,05 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0,05 |
0,05 |
0,1 |
– |
7 |
65 |
0,05 |
0,5 |
0,5 |
0,5 |
0,5 |
0,05 |
0,05 |
0,05 |
0,01 |
0,01 |
0,1 |
0,2 |
0,2 |
0,1 |
– |
8 |
85 |
0,1 |
0,5 |
0,5 |
0,5 |
0,2 |
0,2 |
0,2 |
0,01 |
0,01 |
0,01 |
0,5 |
0,5 |
0,5 |
0,1 |
– |
9 |
60 |
0,03 |
0,5 |
0,5 |
0,5 |
0,2 |
0,2 |
0,2 |
1 |
1 |
1 |
0,03 |
0,03 |
0,03 |
0,1 |
– |
10 |
50 |
0,1 |
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
0,1 |
– |
11 |
75 |
0,05 |
0,2 |
0,2 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,2 |
0,2 |
0,1 |
12 |
65 |
0,02 |
0,1 |
0,1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
0,1 |
0,1 |
0,05 |
13 |
70 |
0,01 |
0,2 |
0,2 |
0,2 |
0,2 |
0,1 |
0,1 |
1 |
1 |
1 |
0,5 |
0,5 |
0,5 |
0,1 |
– |
14 |
50 |
0,01 |
0,1 |
0,1 |
10 |
10 |
10 |
10 |
0,2 |
0,2 |
10 |
10 |
10 |
0,5 |
0,5 |
0,5 |
15 |
85 |
0,01 |
1 |
1 |
5 |
5 |
5 |
5 |
5 |
0,2 |
0,2 |
5 |
5 |
5 |
0,1 |
– |
16 |
80 |
0,1 |
1 |
1 |
2 |
1 |
1 |
5 |
5 |
5 |
3 |
3 |
3 |
1 |
1 |
0,05 |
17 |
95 |
0,1 |
5 |
5 |
1 |
5 |
5 |
10 |
10 |
5 |
5 |
5 |
1 |
1 |
1 |
0,2 |
18 |
60 |
0,01 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0,1 |
– |
19 |
75 |
0,1 |
5 |
5 |
0,5 |
5 |
5 |
1 |
3 |
3 |
1 |
5 |
5 |
0,5 |
5 |
5 |
20 |
90 |
0,1 |
10 |
10 |
10 |
10 |
20 |
20 |
20 |
20 |
20 |
20 |
10 |
10 |
10 |
10 |
21 |
90 |
0,1 |
1 |
1 |
1 |
1 |
0,5 |
0,5 |
0,5 |
2 |
2 |
0,5 |
0,2 |
0,2 |
0,5 |
0,2 |
22 |
80 |
1 |
1 |
1 |
1 |
1 |
0,2 |
0,5 |
0,5 |
1 |
0,5 |
1 |
1 |
1 |
1 |
0,1 |
23 |
70 |
0,5 |
1 |
1,5 |
0,5 |
1 |
1 |
1 |
1,5 |
0,5 |
1,5 |
1,5 |
3 |
3 |
0,1 |
0,1 |
24 |
60 |
1 |
2 |
2 |
2 |
4 |
2 |
2 |
2 |
4 |
5 |
5 |
5 |
5 |
1 |
1 |
25 |
50 |
0,5 |
10 |
10 |
10 |
10 |
0,5 |
5 |
5 |
5 |
5 |
0,8 |
5 |
1 |
1 |
5 |
26 |
60 |
1 |
1 |
2 |
2 |
3 |
5 |
5 |
5 |
5 |
2 |
2 |
5 |
5 |
5 |
1 |
27 |
70 |
0,5 |
0,5 |
0,5 |
1 |
1 |
1 |
1,5 |
1,5 |
1,5 |
1 |
1 |
1 |
1 |
1,5 |
1 |
28 |
80 |
1 |
2 |
2 |
2 |
2 |
2 |
5 |
5 |
5 |
5 |
5 |
2 |
1 |
1 |
1 |
29 |
90 |
0,5 |
2 |
2 |
2 |
2 |
5 |
5 |
5 |
5 |
3 |
3 |
3 |
3 |
1 |
1 |
30 |
80 |
2 |
1 |
2 |
1 |
5 |
5 |
2 |
5 |
5 |
2 |
1 |
2 |
1 |
2 |
1 |
31 |
70 |
2 |
1 |
2 |
1 |
5 |
5 |
2 |
5 |
5 |
2 |
1 |
2 |
1 |
2 |
1 |
32 |
60 |
5 |
5 |
2 |
2 |
2 |
5 |
5 |
1 |
1 |
2 |
2 |
3 |
3 |
1 |
1 |
33 |
60 |
1 |
2 |
3 |
3 |
4 |
2 |
2 |
3 |
3 |
3 |
5,5 |
5,5 |
5,5 |
0,2 |
0,5 |
34 |
90 |
0,6 |
0,3 |
0,3 |
0,6 |
0,6 |
0,3 |
0,3 |
0,6 |
0,2 |
0,2 |
0,2 |
0,2 |
1 |
1 |
1 |
35 |
95 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
36 |
80 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
37 |
70 |
1 |
1 |
1 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
0,5 |
0,5 |
0,2 |
0,2 |
0,2 |
38 |
90 |
3 |
3 |
3 |
2 |
2 |
1 |
1 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
2 |
39 |
90 |
8 |
8 |
8 |
8 |
3 |
3 |
3 |
3 |
5 |
5 |
5 |
5 |
2 |
2 |
2 |
40 |
80 |
2 |
2 |
2 |
2 |
5 |
5 |
8 |
2 |
2 |
2 |
2 |
5 |
5 |
8 |
8 |