Порядок выполнения работы Методика обработки статистической информации о ресурсе машины с помощью MathCad

1.Исходную информацию о ресурсе машины записываем в текстовый файл в виде колонки чисел, в том же каталоге, где находится протокол MathCad, используя простейший редактор Windows "Блокнот".

2.После этого вводим информацию в протокол MathCad с помощью функции READPRN и определяем количество информации с помощью функции length. Предварительно переменной MyFile присваиваем имя текстового файла с данными о ресурсах машин.

где Х - вектор наработок на отказ исследуемого элемента автомобиля, км пробега в порядке возрастания его элементов;

N – количество информации, длина вектора.

3. Строим вариационный ряд, расположив информацию о ресурсе машины в порядке возрастания с помощью функции sort и присваиваем каждому элементу вектора индекс j

4.Определяем точечные характеристики распределения ресурса

- определяем общее число интервалов n в статистическом ряду по формуле

где nd- количество дополнительных интервалов,

- рассчитываем величину интервала

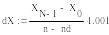
- рассчитываем величину смещения распределения

- определяем среднее значение наработки

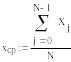
- рассчитываем среднеквадратическое отклонение,

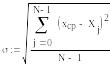
- рассчитываем коэффициент вариации наработки на отказ

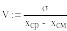
5. Проверяем информацию на выпадающие точки с помощью критерия Ирвина

- рассчитываем значение критерия Ирвина для минимального ресурса в вариационном ряду информации

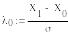
- рассчитываем значение критерия Ирвина для максимального ресурса в вариационном ряду информации

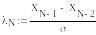
- рассчитываем критическое значение критерия Ирвина для вероятности 0,99 по эмпирической формуле

Если расчетное значение критерия Ирвина для ресурса больше критического, то минимальное или максимальное его значение является выпадающей точкой и его следует удалить из исходной информации (из текстового файла с исходной информацией) и расчет повторить заново.

Очистку информации от выпадающих точек продолжаем до тех пор, пока не будет выполнено условие

₀_КР и _N-1_КР.

6. Выбраем теоретический закон распределения.

6.1. По коэффициенту вариации принимаем закон распределения ресурса машины: закон нормального распределения или закон распределения Вейбулла, так как коэффициент вариации находится в пределах 0,33 – 0,7.

6.2. Закон распределения можно выбрать визуально на основании сравнения полигона распределения и дифференциальных функций законов, принятых в п. 6.1.

Для этого строим графики, предварительно определив частоту попаданий в каждый интервал m, используя функцию MathCad hist, и присваиваем индекс интервалам i.

Создаем также вектор начальных Xn, конечных Xk и средних значений Xc для каждого интервала интервалов

Результаты расчетов представляем в виде векторов значений

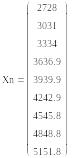
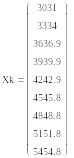
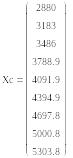
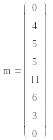
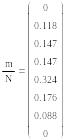
Определяем накопленные опытные вероятности mS_z, соответствующие конечным наработкам интервалов, предварительно присвоив им индекс z

Строим графики по опытным данным (рис.1.2):

- гистограмму (ступенчатый график) и полигон распределения (ломаная кривая) m/N по частости, опытной вероятности m/N

- кривую накопленных опытных вероятностей mS Рассчитываем значения теоретических функций для интервалов.

Дифференциальную функцию нормального закона распределения рассчитать по формуле

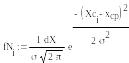
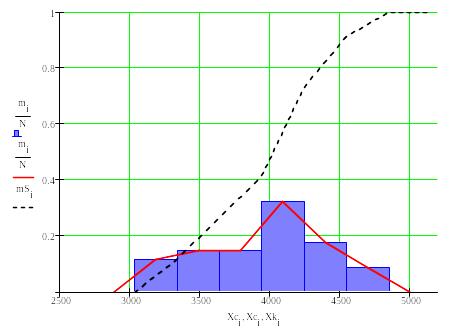
Рис. 1.2. Опытные кривые распределения ресурса машины

Перед расчетом дифференциальной функции закона Вейбулла определяем параметры этого закона:

- параметр формы закона Вейбулла b определяем по формулам, полученным путем аппроксимации табличных данных

- масштабный параметр a рассчитываем, предварительно определив коэффициент Kb по формуле

.

Дифференциальную функцию закона распределения Вейбулла рассчитываем по формуле

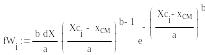
Результаты расчета представляем в виде векторов, с использованием которых строим график (рис.1. 3)

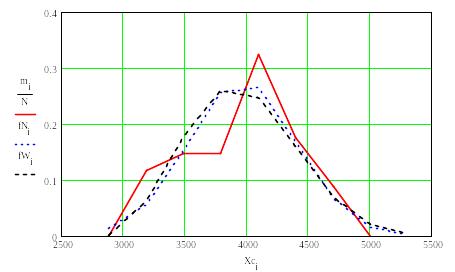
Рис. 1.3. Полигон распределения и дифференциальные функции теоретических законов (ЗНР и ЗРВ)

6.3. Для более точного выбора закона распределения целесообразно использовать критерий Пирсона χ²

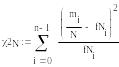
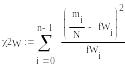
Допустимая вероятность совпадения опытных данных с расчетными по критерию χ² равна 10%:.

Требуемый уровень значимости принимаем равным ε:=0,15.

Число степеней свободы определяем по выражению

Расчетные вероятности совпадения опытных данных с теоретическими

- для нормального закона распределения

- для закона распределения Вейбулла

Таким образом, закон распределения Вейбулла, имеющий большую вероятность, принимаем как закон распределения ресурса машины

7. Определяем интервальные характеристики распределения ресурса генеральной совокупности машин

При расчете интервальных оценок распределения задаться доверительной вероятностью, например 0,95

.

Затем используем известные формулы и встроенные функции MathCad для определения квантилей закона распределения Стьюдента и Вейбулла. При количестве информации менее 100 вместо нормального закона распределения рекомендуется использовать закон распределения Стьюдента.

- доверительные границы одиночного значения показателя надежности для нормального закона распределения

где qt(α, N) – встроенная функция MathCad, позволяющая определить квартиль распределенияя при заданной доверительной вероятности α и количестве информации N.

- доверительные границы одиночного значения показателя надежности для закона распределения Вейбулла

Доверительные границы среднего значения ресурса определяем, не зависимо от теоретического распределения, по выражению

Верхняя доверительная одностороння граница среднего значения ресурса машины

Относительную предельную ошибку переноса определяем при односторонней доверительной вероятности ₀=(1+)/2. Относительная ошибка не должна превышать 10-20%.
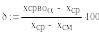