Методика проведения занятия

1. Обучающиеся самостоятельно изучают теоретическую часть.

2. Под руководством преподавателя обучающиеся рассчитывают коэффициенты парной корреляции по исходным данным, гипотетически полученным при выполнении лабораторной работы №1 и приведенным в табл. 2.4.

Таблица 2.4

Значения измеренных диагностических параметров

y i u	n1	n2	n3	n4	n5	n6	n7	n8	n9	n10
y1u	13,2	12,8	13	12,5	11,5	12,8	12,9	13,1	13,3	12,4
y2u	10,5	10	10,4	10,6	9,5	9,8	9	11	9,7	11,1
y3u	0,11	0,08	0,6	0,22	0,15	0,1	0,12	1	0,25	0,09
y4u	15,5	14	16	13,5	12,5	14	11,5	13,9	12,6	13
y5u	700	1100	750	1000	720	980	730	650	690	900
y6u	38	56	50	42	68	58	38	64	72	46
y7u	40	56	50	43	70	60	41	66	52	44
y8u	35	55	50	45	65	75	45	65	50	48

В табл. 2.4 n_i соответствуют номерам измерений следующих диагностических параметров y _{i u} :

y_1u – напряжение аккумуляторной батареи без нагрузки (при включенных потребителях), В;

y_2u – напряжение аккумуляторной батареи под нагрузкой (работа стартера без заводки автомобиля), В;

y_3u – переходное сопротивление контактов прерывателя, В;

y_4u – напряжение на контактах «Б» и «Ш» реле-регулятора, В;

y_5u – минимально устойчивая частота вращения коленчатого вала двигателя (КВД), мин^-1;

y_6u – угол замкнутого состояния контактов прерывателя при 1000 мин^-1;

y_7u - угол замкнутого состояния контактов прерывателя при максимальных оборотах двигателя, мин^-1;

y_8u – падение частоты вращения КВД при отсоединении шланга принудительной вентиляции двигателя, мин^-1.

Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 г. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон. В общем случае расчетные формулы будут иметь следующий вид:

y _{i u} = y_{i u} / n ;

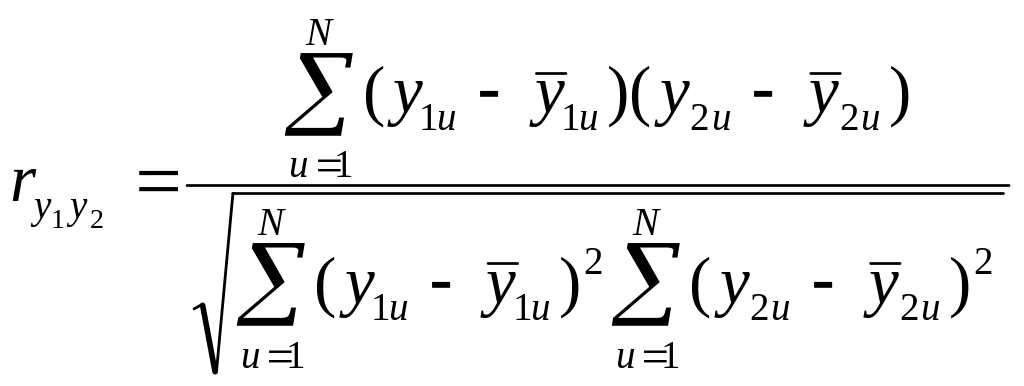
Для расчетов используем программу PEARSON EXEL и персональный компьютер. Последовательность расчета коэффициентов корреляции между диагностическими параметрами y_1u и y_4u показана на рис. 2.1…2.3.

Рассчитанный коэффициент корреляции Пирсона получился равным: r_1,4 = 0,364999. Его значение может лежать в пределах [-1;+1]. Для проверки значимости коэффициента парной корреляции его величину необходимо сравнить с критическим значением r (см. табл. 2.3). Найдем число степеней свободы f = n – 2; n - число наблюдений (в нашем случае n= 10) => f = 8 получаем критическое значение r = 0,632. Критическое значение r = 0,632 больше рассчитанного коэффициента корреляции

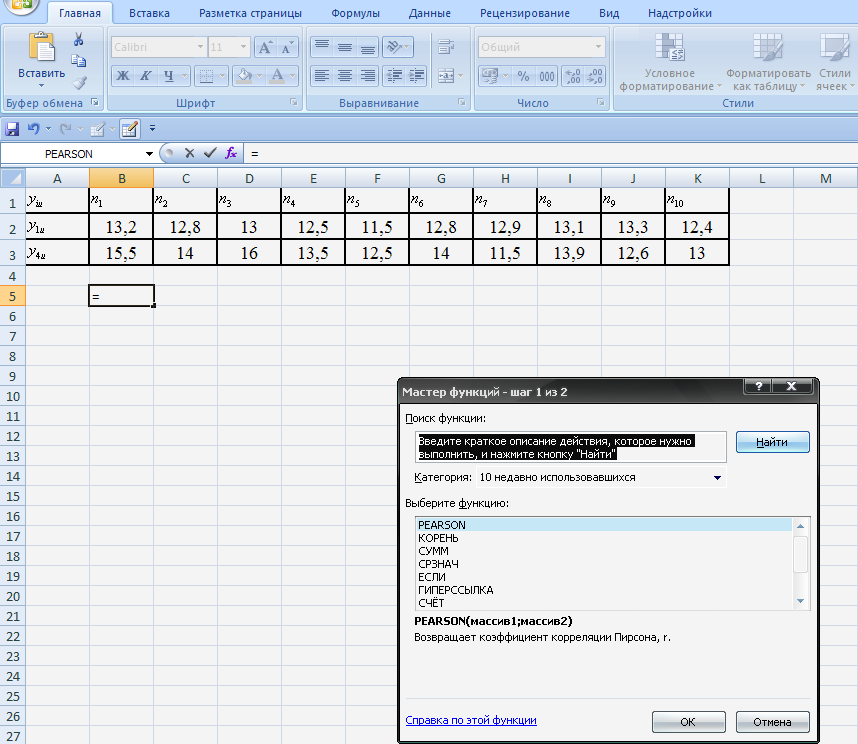
Рис. 2.1. Ввод исходных данных

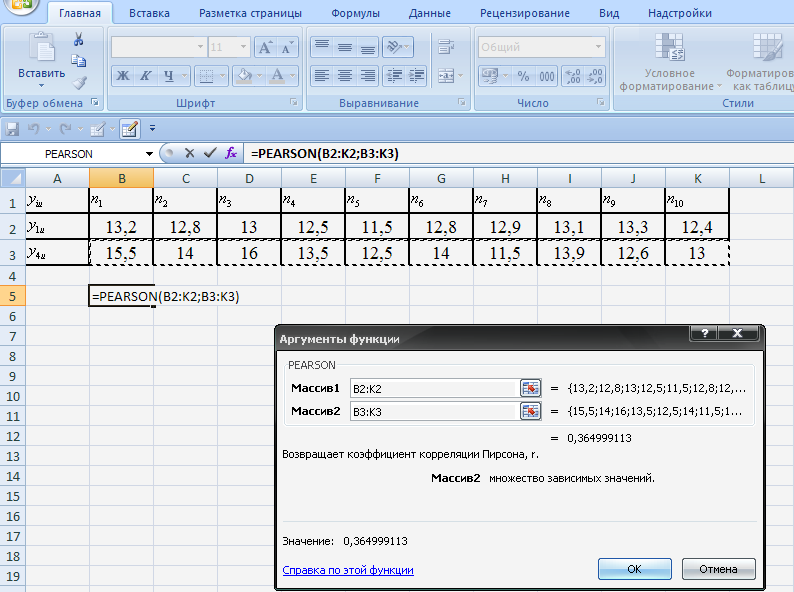
Рис. 2.2. Формирование массивов

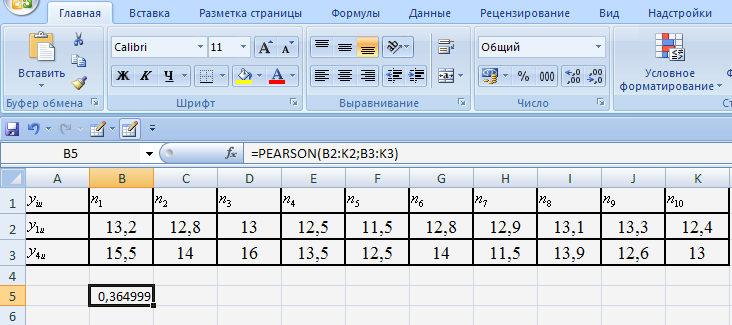
Рис. 2.3. Результат расчета

Пирсона, r = 0,36499 следовательно эти величины между собой линейно независимы. Если бы мы получили расчетное значение коэффициента корреляции со знаком «-» это бы говорило о том, что СВ находятся в обратной связи, т.е. при увеличении одной вторая бы уменьшалась. В конце занятия обучающиеся индивидуально сообщают преподавателю о полученных результатах, представляя расчеты и делая вывод о наличии или отсутствии линейной связи между всеми рассмотренными диагностическими параметрами.