Расчет многопролетного ригеля

Нагрузка

Назначаем размеры сечения ригеля. Высота сечения

h_b=L_r/12=6.2/12=0,53≈ 0.6 м (округлять с точностью 0,1м),

ширина

b_b=0_,4×h_b=0,4×0,6=0,24 ≈ 0,25 м (точность – 0,05 м ).

Постоянная g=g_p+g_b=γ_n*g_pc*a+γ_f*γ_n*γ_rc*b_b*h_b=0.95*4.134*6,0+1.1*0.95*25*0.25*0.6= 27,48 кН/м

Временная υ=γ_n*γ_f*υ_p*a=0.95*1.2*7,2*6,0=49,25 кН/м.

Полная q=g+v=27,48+49,25=76,73 кН/м.

Построение эпюр усилий в ригеле

Сначала вычисляем эпюрные моменты от четырех элементарных загружений

1. нагрузка g распределенная по всем трем пролетам;

2. нагрузка v, приложенная в первом и третьем, считая слева, пролетах рамы;

3. то же, во втором пролете;

4. то же в первом и втором пролетах.

Для схемы 1 вычислим М₁₂

Отношение погонных жесткостей ригеля и колонны

таб.1. Вычисление опорных моментов ригеля при различных схемах загружения.

Исходные данные: L_b=6,4; k=1,5; k₁=2; k₂=3

Формулы вычислений:

;

нагрузка		элементарная				комбинированная
Схема загружения	номер	1	2	3	4	1+2	1+3	1+4
1	2	3	4	5	6	7	8	9
		27,48	76,73	76,73	76,73
Опора 1	α1	-0,063	-0,070	0,007	-0,062
	α2	-0,054	-0,062	0,008	-0,052
	α	-0,0585	-0,066	0,0075	-0,057
	М12	-65,8	-207	24	-179,1	-272,8	-41,8	-244,9
Опора 2, слева	α1	-0,091	-0,074	-0,017	-0,095
	α2	-0,093	-0,068	-0,025	-0,101
	α	-0,092	-0,071	-0,021	-0,098
	М21	-104	-223	-66	-308	-327	-170	-412
Опора 2, справа	α1	-0,085	-0,012	-0,073	-0,094
	α2	-0,087	-0,018	-0,069	-0,098
	α	-0,086	-0,015	-0,071	-0,096
	М23	-98	-47,1	-223	-301,7	-145,1	-321	-399
Опора 3, слева	α1	-0,085	-0,012	-0,073	-0,066
	α2	-0,087	-0,018	-0,069	-0,059
	α	-0,086	-0,015	-0,071	-0,0625
	М32	-98	-47,1	-223	-196,4	-145,1	-321	-294,4

Вывод усилий в пролетах

а) нагружение «1+2»

Для пролета 1:

проверка: х=L_b=6.4 м; М=-272,8+237,1*6,4-38,37*6,4²=-327 кНм=М₂₁

Q=dM/dx=(-272,8+237,1x-38,37x²)=237,1-76,73x кН

Х_max=237,1/76,73=3.1 м

Для пролета 2:

проверка: х=L_b=6.4 м; М=-145,1+87,9*6,4-13,74*6,4²=-145,1 кНм=М₃₂

Q=dM/dx=(-145,1+87,9x-13,74x²)=87,9-27,48x кН

Х_max=87,9/27,48=3.2 м

а) нагружение «1+3»

Для пролета 1:

проверка: х=L_b=6.4 м; М=-41,8+67,9*6,4-13,74*6,4²=-170 кНм=М₂₁

Q=dM/dx=(-41,8+67,9x-13,74x²)=67,9-27,4x кН

Х_max=67,9/27,48=2,5 м

Для пролета 2:

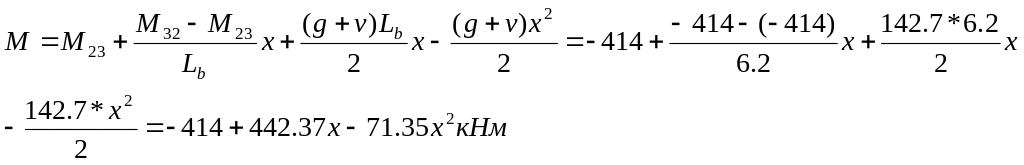
проверка: х=L_b=6.4 м; М=-321+245,5*6,4-38,37*6,4²=-321 кНм=М₃₂

Q=dM/dx=(-321+245,5x-38,37x²)=245,5-76,73x кН

Х_max=245,5/76,73=3.2 м

а) нагружение «1+4»

Для пролета 1:

проверка: х=L_b=6.4 м; М=-244,9+219,4*6,4-38,37*6,4²=-412 кНм=М₂₁

Q=dM/dx=(-244,9+219,4x-38,37x²)=219,4-76,73x кН

Х_max=219,4/76,73=2,9 м

Для пролета 2:

проверка: х=L_b=6.4 м; М=-399+229,2*6,4-38,37*6,4²=-294 кНм=М₃₂

Q=dM/dx=(-399+229,14x-38,37x²)=229,14-76,73x кН

Х_max=229,14/76,73=3 м

Использование метода предельного равновесия при расчете многоэтажных рам заключается в «выравнивании» эпюры моментов загружения «1+4». Под данным термином понимается процедура снижения опорного момента М₂₁ примерно на 30%, но только до значения максимальных моментов на опоре 2 при нагружениях «1+2» и «1+3», приравнивания момента М₂₃ новому значению М₂₁. происходящие при этом перераспределение усилий учитывается увеличением моментов М₁₂ и М₃₂ на ⅓ уменьшения М₂₁ и М₂₃, соответственно.

30 % снижение составит ΔМ₂₁=0,3*М₂₁=0,3*(-412)=-123,6 кНм

при этом М₂₁=М_21(1+4)-ΔМ₂₁=-412-(-123,6)=-288,4 кНм, что меньше среднего значения максимального момента на опоре 2 при нагружениях «1+2» и «1+3».

М₂^/=(М_21(1+2)+М_23(1+3))/2= (-327+(-321))/2=-324 кНм

Поэтому принимаем ΔМ₂₁=М_21(1+4)-М₂^/=-412-(-324)=-88 кНм.

Тогда: М₂₁=М_21(1+4)-ΔМ₂₁=-412-(-88)=-324 кНм

М₂₃=М₂₁=-324 кНм

М₁₂=М_12(1+4)+ΔМ₂₁/3=-244,9+(-88)/3=-274,2 кНм

При снижении момента М₂₃ на ΔМ₂₃=М_23(1+4)-М₂₁=-399-(-324)=75 кНм, новый момент на опоре 3

М₃₂=М_32(1+4)+ΔМ₂₃/3=-399+(-75)/3=-424 кНм

а) нагружение «1+4в»

Для пролета 1:

проверка: х=L_b=6.4 м; М=-274,2+237,8*6,4-38,37*6,4²=-324 кНм=М₂₁

Q=dM/dx=(-274,2+237,8x-38,37x²)=237,8-76,73x кН

Х_max=237,8/76,73=3,1 м

Для пролета 2:

проверка: х=L_b=6.4 м; М=-324+230*6,4-38,37*6,4²=-424 кНм=М₃₂

Q=dM/dx=(-324+230x-38,37x²)=230-76,73x кН

Х_max=230/76,73=3 м