Признаки делимости

– Вспомним известные нам признаки делимости в форме викторины «Верно ли, что…»

1. На 2 делятся все четные числа? (Да)

2. На 3 делятся числа, сумма цифр которых кратна 3? (Да)

3. На 4 делятся числа, две последние цифры которых нули или числа, не кратные 4? (Нет! На 4 делятся числа, две последние цифры которых нули или числа, кратные 4!)

4. На 5 делятся числа, оканчивающиеся на 5 или на 0? (Да)

5. На 6 делятся числа, которые делятся на 3? (Нет! На 6 делятся числа, которые делятся на 2 и на 3 одновременно! 81 делится на 3, но не делится на 6!)

6. Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7? (Да. 259 делится на 7 т.к. 25–(9*2)=25–18=7 делится на 7; 324 не делится на 7 т.к. 32–(4*2)=32–8=24 не делится на 7)

7. На 8 делятся числа, три последние цифры которых нули или числа, кратные 8? (Да)

8. На 9 делятся числа, сумма цифр которых кратна 3? (Нет! На 9 делятся числа, сумма цифр которых кратна 9!)

9. На 10 делятся числа, оканчивающиеся 0? (Да)

10. На 11 делятся числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11? (Да. 105787 делится на 11 т.к. 1+5+8=14 и 0+7+7=14, 14=14)

11. На 12 делятся числа, которые делятся на 4? (Нет! На 12 делятся числа, которые делятся на 3 и на 4 одновременно!)

12. Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13? (Да. 845 делится на 13, так как 84+(4*5) = 104 делится на 13)

13. На 14 делится числа, которые делятся на 7? (Нет! На 14 делятся числа, которые делятся на 2 и на 7 одновременно.

14. На 15 делится числа, которые делятся на 3 и на 5 одновременно? (Да)

15. На 25 делятся числа, две последние цифры которых нули или составляют число, кратное 25? (Да)

16. На разрядную единицу делятся числа, у которых количество нулей больше количества нулей разрядной единицы? (Нет! На разрядную единицу делятся числа, у которых количество нулей больше или равно количеству нулей разрядной единицы.)

–Делятся ли, следующие числа на 6, 9, 11 или 13? (1026, 151632, 35805, 9163627, 1710, 113724);

–(стр.61 №90) Ковбой Джо зашел в бар и попросил у бармена бутылку виски за 3 доллара, трубку за 6 долларов, 3 пачки табака и 9 коробок непромокаемых спичек, цену которых он не знал. Бармен потребовал 11 долларов и 80 центов, на что Джо вытащил револьвер. Бармен поторопился исправить ошибку. Как Джо догадался, что бармен хотел его обсчитать?

(–Стоимость всех покупок делиться на 3, а бармен назвал сумму не делящуюся на 3.)

–(стр.79 №117) Число делится на 7 тогда и только тогда, когда делится на 7.

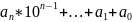(–Запишем данное число по-другому = =10( =7( +3( =7( )+3 . Первое из 2ух слагаемых делится на 7; сумма будет делиться на 7 тогда и только тогда, когда и 2ое слагаемое будет делиться на 7. А это возможно тогда и только тогда, когда делится на 7.)

– Делятся ли на 7 следующие числа?(259, 3245, 13265)