Дифференцирование функций, заданных параметрически
Пусть функции x = (t) и y = ψ(t) определены на некотором отрезке [α, β]. Переменную t будем называть параметром.
Если x = (t) взаимно однозначна на отрезке [α, β], то она имеет обратную функцию t(x) = − 1 (x). Подставляя ее в равенство y = ψ(t), видим, что переменная y является сложной функцией переменной x:
|
y = ψ( − 1 (x) ) ≡ f(x) . |
|
В этом случае говорят, что функция y = f(x) задана параметрически уравнениями
|
|
(1) |
где t [α, β].
Производная первого порядка функции, заданной параметрически
Теорема 1. Пусть функция y = f(x) задана параметрически уравнениями (1), причем функции (t) и ψ(t) дифференцируемы в некоторой точке t0 (α, β), и '(t0) ≠ 0.
Тогда функция y = f(x) дифференцируема в точке x0 = (t0), причем
|
f '(x0) =
|
(2) |
Доказательство.
В условиях теоремы функция (t) имеет дифференцируемую обратную функцию t(x) = − 1 (x), производная которой в точке x0 = (t0) определяется формулой
|
t '(x) =
. |
|
Дифференцируя f(x) = ψ(t(x)) в точке x0 = (t0) как сложную функцию x, при t = t0 получаем
|
f'(x0) = ψ'(t) · t'(x) =
. |
|
Производная второго порядка функции, заданной параметрически
Если функции (t) и ψ(t) дважды дифференцируемы в некоторой точке t0 (α, β) и '(t0) ≠ 0, то
|
f ''(x0) =
. |
|
Возрастание и убывание функции
функция y = f (x) называется возрастающей на отрезке [a, b], если для любой пары точек х и х', а ≤ х < х' ≤ b выполняется неравенство f(x) ≤ f (x'), и строго возрастающей — если выполняется неравенство f (x) < f (x'). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х2 (рис., а) строго возрастает на отрезке [0,1], а
(рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x)↑, а убывающие f (x)↓. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].
Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x0, если найдётся такой интервал (α, β), содержащий точку x0, что для любой точки х из (α, β), х> x0, выполняется неравенство f (x0) ≤ f (x), и для любой точки х из (α, β), х< x0, выполняется неравенство f (x) ≤ f (x0). Аналогично определяется строгое возрастание функции в точке x0. Если f'(x0) > 0, то функция f (x) строго возрастает в точке x0. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 1, М., 1966.
С. Б. Стечкин.
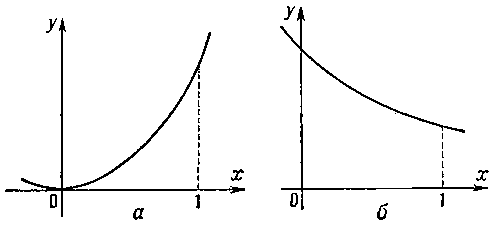
Возрастание и убывание функции
функция y = f (x) называется возрастающей на отрезке [a, b], если для любой пары точек х и х', а ≤ х < х' ≤ b выполняется неравенство f(x) ≤ f (x'), и строго возрастающей — если выполняется неравенство f (x) < f (x'). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х2 (рис., а) строго возрастает на отрезке [0,1], а
(рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x)↑, а убывающие f (x)↓. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].
Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x0, если найдётся такой интервал (α, β), содержащий точку x0, что для любой точки х из (α, β), х> x0, выполняется неравенство f (x0) ≤ f (x), и для любой точки х из (α, β), х< x0, выполняется неравенство f (x) ≤ f (x0). Аналогично определяется строгое возрастание функции в точке x0. Если f'(x0) > 0, то функция f (x) строго возрастает в точке x0. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 1, М., 1966.
С. Б. Стечкин.