Логарифмическая производная
Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.
Пример 11
Найти
производную функции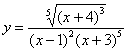 
Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.
Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:
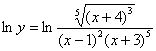
Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:
Собственно приступаем к дифференцированию. Заключаем под штрих обе части:
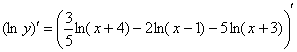
Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.
Как быть с левой частью?
В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».
Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :
В левой
части как по мановению волшебной палочки
у нас «нарисовалась» производная 
.
Далее по правилу пропорции перекидываем
«игрек» из знаменателя левой части
наверх правой части:
А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:
Окончательный
ответ:
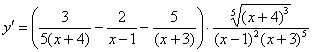
Пример 12
Найти
производную функции 
Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.
С помощью логарифмической производной можно было решить любой из примеров №№4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.
Производные и дифференциалы высших порядков
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производнойфункции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
Производные n-го порядка от основных элементарных функций
Справедливы формулы
Формула Лейбница
Если u и v - n-кратно дифференцируемые функции, то
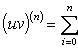
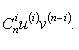
Производные n-го порядка вектор-функции, комплекснозначной и матричной функций
Если
компоненты 
n-кратно
дифференцируемы, то 
.
Аналогично для комплекснозначной функции f и матричной функции A имеем формулы:
f(n)(x) = u(n)(x) + iv(n)(x); dnf(x) = dnu(x) + idnv(x);
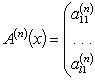
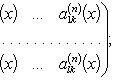
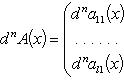
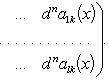
Лейбница формула
формула, выражающая производную n-го порядка (см. Дифференциальное исчисление) от произведения двух функций через производные сомножителей:
.