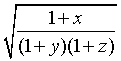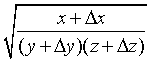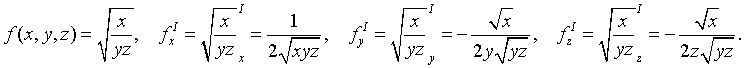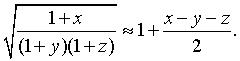- •Бесконечно малая последовательность[править]
- •§ 128. Монотонные последовательности
- •Число е
- •1.3.6. Предел функции
- •Критерий Коши существования предела функции в точке.
- •Замечательные пределы. Примеры решений
- •Первый замечательный предел
- •Второй замечательный предел
- •Определение непрерывности функции
- •§ 3.7. Равномерная непрерывность функции
- •Производная сложной функции. Примеры решений
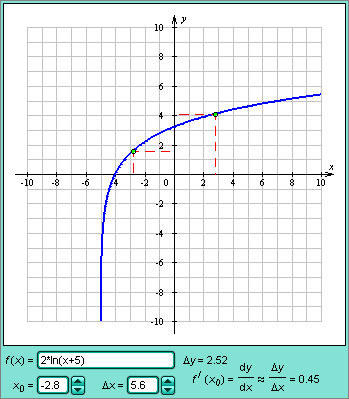
- •Производная функции. Геометрический смысл производной
- •3.1.3. Дифференциал функции
- •Дифференцирование сложной функции. Дифференцирование обратной функции.
- •Логарифмическая производная
- •Производные и дифференциалы высших порядков
- •Дифференцирование функций, заданных параметрически
- •Формула Лагранжа.
- •Промежутки монотонности функции
- •Конечных приращений формула Значение слова "Конечных приращений формула"
- •Раскрытие неопределённостей вида , Определение («на языке последовательностей», или по Гейне)
- •Определение (на «языке ε-δ», или по Коши»)
- •Основные теоремы о пределах
- •Неопределённость вида
- •Неопределённость вида
- •Тейлора формула
- •Достаточные условия экстремума
- •Выпуклость, вогнутость функции, точка перегиба.
- •Нахождение интервалов выпуклости функции.
- •Необходимое и достаточные условия перегиба. Необходимое условие перегиба.
- •Первое достаточное условие перегиба.
- •Второе достаточное условие перегиба.
- •Третье достаточное условие перегиба.
- •Асимптоты графика функции
- •Общая схема исследования функции и построения её графика
3.1.3. Дифференциал функции
Итак,
график дифференцируемой функции в
окрестности каждой своей точки сколь
угодно близко приближается к графику
касательной в силу равенства:![]() где
α – бесконечно малая в окрестности
где
α – бесконечно малая в окрестности ![]() функция.
Для приближенного вычисления значения
функции f в
точке x0 + Δx эту
бесконечно малую функцию можно
отбросить:
функция.
Для приближенного вычисления значения
функции f в
точке x0 + Δx эту
бесконечно малую функцию можно
отбросить:
|
Линейную
функцию ![]() называют дифференциалом
функции f в
точке
и
обозначают df.
Для функции x производная
в каждой точке
равна 1,
то есть
называют дифференциалом
функции f в
точке
и
обозначают df.
Для функции x производная
в каждой точке
равна 1,
то есть ![]() Поэтому
пишут:
Поэтому
пишут:
|
Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
|
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
![]()
|
Модель 3.3. Дифференциал функции |
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx.
Дифференцирование сложной функции. Дифференцирование обратной функции.
Пусть функция u=g(x) определена на множестве X и U — область ее значений. Пусть, далее, функция y=f(u) определена на множестве U. Поставим в соответствие каждому x из X число f(g(x)). Тем самым на множестве X будет задана функция y=f(g(x)). Ее называют композицией функций или сложной функцией.
Если известна производная функции f(x), то производную сложной функции f(u) можно вычислить с помощью следующей формулы:
(f(u))'=f '(u)⋅u'
Пример:
1) Вычислить производную функции (x+2)10. Обозначим u=x+2.
Так как (x10)'=10x9, то((x+2)10)'=(u10)'=10u9⋅u'=10(x+2)9⋅1=10(x+2)9
2) Вычислить производную функции f(x)=sin(cos x). Обозначим u=cos x.
(sin x)'=cos x, поэтому
(sin(cos x))'=(sin u)'=cos u⋅u'==cos(cos x)⋅(cos x)'==cos(cos x)⋅(−sin x)==−cos(cos x)⋅sin x
3) Вычислить производную функции ln cos x2. Обозначим u=cos x2.
(ln x)'=1x, поэтому (ln cos x2)'=(ln u)'=1u⋅u'=u'u=(cos x2)'cos x2.
Таким же образом вычислим производную функции cos x2. Снова обозначим u=x2.
(cos x2)'=(cos u)'=−sin u⋅u'=−sin x2⋅(x2)'=−2x sin x2.
Далее, вставив полученное выражение, получается
(ln cos x2)'=−2x sin x2cos x2 = −2x tg x2
Используя правило дифференцирования сложной функции, можно обосновать правило дифференцирования обратной функции.
Зная производную функции y=f(x), можно производную обратной функции x=g(y)найти по формуле:
xy′=1yx′
(разумеется, при условии, что f′(x)≠0).
Применение полного дифференциала в приближенных вычислениях
1.
Составьте формулу, дающую при малых
абсолютных значениях величин x, y, z
приближённое выражение
Решение: Так как найти полный дифференциал легче, чем полное приращение функции, то в вычислениях используют приближенную формулу:
где
в виде:
,где x=1; y=1 и z=1, а x, y и z заменю на Δx, Δy и Δz Для приближённого вычисления значения функции трёх переменных можно использовать формулу:
Получу приближённое значение (x=1, y=1, z=1):
Для исходного выражения получим результат:
|
Правила дифференцирования суммы, произведения и частного двух дифференцируемых функций.
Теорема Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы: 1) (u±v)/=u/±v/ , 2) (u·v)/=u/v+v/u , 3) (vu)=v2u/v−v/u .
Доказательство Из определения производной:
(u±v)/=limΔx→0Δx[u(x+Δx)±v(x+Δx)]−[u(x)±v(x)]= =limΔx→0Δx[u(x+Δx)−u(x)]±[v(x+Δx)−v(x)]= .
=limΔx→0Δxu(x+Δx)−u(x)±limΔx→0Δxv(x+Δx)−v(x)=u/±v/
(u·v)/=limΔx→0Δxu(x+Δx)·v(x+Δx)−u(x)·v(x)±v(x+Δx)·v(x)= limΔx→0Δxu(x+Δx)[v(x+Δx)−v(x)]+
+limΔx→0Δxv(x)[u(x+Δx)−u(x)]=uv/+vu/.
(vu)/=limΔx→0Δxv(x+Δx)u(x+Δx)−v(x)u(x)=limΔx→0Δx·v(x+Δx)·v(x)u(x+Δx)·v(x)−u(x)·v(x+Δx)±u(x)·v(x)=v2u/v−v/u.