- •Бесконечно малая последовательность[править]
- •§ 128. Монотонные последовательности
- •Число е
- •1.3.6. Предел функции
- •Критерий Коши существования предела функции в точке.
- •Замечательные пределы. Примеры решений
- •Первый замечательный предел
- •Второй замечательный предел
- •Определение непрерывности функции
- •§ 3.7. Равномерная непрерывность функции
- •Производная сложной функции. Примеры решений
- •Производная функции. Геометрический смысл производной
- •3.1.3. Дифференциал функции
- •Дифференцирование сложной функции. Дифференцирование обратной функции.
- •Логарифмическая производная
- •Производные и дифференциалы высших порядков
- •Дифференцирование функций, заданных параметрически
- •Формула Лагранжа.
- •Промежутки монотонности функции
- •Конечных приращений формула Значение слова "Конечных приращений формула"
- •Раскрытие неопределённостей вида , Определение («на языке последовательностей», или по Гейне)
- •Определение (на «языке ε-δ», или по Коши»)
- •Основные теоремы о пределах
- •Неопределённость вида
- •Неопределённость вида
- •Тейлора формула
- •Достаточные условия экстремума
- •Выпуклость, вогнутость функции, точка перегиба.
- •Нахождение интервалов выпуклости функции.
- •Необходимое и достаточные условия перегиба. Необходимое условие перегиба.
- •Первое достаточное условие перегиба.
- •Второе достаточное условие перегиба.
- •Третье достаточное условие перегиба.
- •Асимптоты графика функции
- •Общая схема исследования функции и построения её графика
График
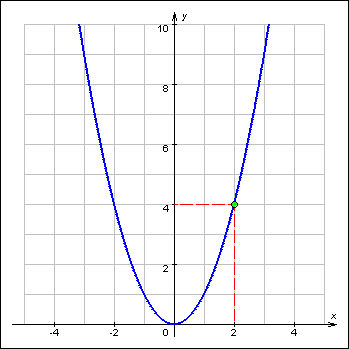
1.3.6.1.
Предел
функции y = x2 при x → 2.
График
1.3.6.2.
Предел
функции Если A –
предел функции в точке a,
то пишут, что
Определения
предела функции по Коши и по Гейне
эквивалентны.
График
1.3.6.3.
Предел
функции y = {x (x ≠ 0); 1 (x = 0)} приx → 0 равен 0. Предел
функции Если
функция f (x) имеет
предел в точке a,
то этот предел единственный.
Число A1 называется пределом
функции f (x) слева в
точке a,
если для каждого ε > 0 существует
δ > 0 такое, что для всех
Число A2 называется пределом
функции f (x) справа в
точке a,
если для каждого ε > 0 существует
δ > 0 такое, что для всех
Предел слева
обозначается Если
для каждого ε > 0 существует такая
δ-окрестность точки a,
что для всех x,
удовлетворяющих условию |x – a| < δ, x ≠ a,
выполняется неравенство |f (x)| > ε,
то говорят, что функция f (x) имеет
в точке a бесконечный
предел:
Так,
функция Если
для каждого ε > 0 существует такое
δ > 0, что для любого x > δ
выполняется неравенство |f (x) – A| < ε,
то говорят, что предел функции f (x) при x,
стремящемся к плюс бесконечности,
равен A:
Аналогично
формулируется определение предела
при x,
стремящемся к минус бесконечности: Наконец,
запись Если
функция f (x) имеет
конечный предел в точке a,
то существует окрестность точки a,
в которой функция f ограничена
( возможно, что в самой точке a функция
не определена). При этом, если A ≠ 0,
то найдется окрестность точки a,
в которой (быть может, за исключением
самой точки a) значения
функции f имеют
тот же знак, что и числоA. Если
существует такое δ > 0, что для
всех x,
принадлежащих δ-окрестности точки a,
выполняются неравенства
g (x) ≤ f (x) ≤ h (x), и
если
то
существует Если
существует такое δ > 0, что для
всех x,
принадлежащих δ-окрестности точки a,
справедливо неравенство
f (x) < g (x), и
если Если
функции f (x) и g (x) имеют
конечные пределы в точке a,
причем
то
Из
существования пределов f (x) в
точке a и g (y) в
точке f (a) следует
существование предела сложной
функции g (f (x)) в
точке a.
Для вычисления
пределов часто используют так
называемые замечательные
пределы:
Доказательство
Другие
важные пределы (при a > 0, a ≠ 1):
следуют
из замечательных пределов и свойства
предела обратной функции.
Функция
α (x) называется бесконечно
малой при x → a (здесь a –
конечное число или ∞),
если
Сумма
конечного числа бесконечно малых
при x → a функций
есть бесконечно малая функция.
Произведение
бесконечно малой при x → a функции
на ограниченную в некоторой окрестности
точки a функцию
есть бесконечно малая при x → a функция.
Если в
некоторой окрестности a определены
функции f (x), g (x), h (x) такие,
что f (x) = g (x) h (x),
f (x) ~ g (x). Так,
функции
sin x ~ x
tg x ~ x
arcsin x ~ x
arctg x ~ x
ex – 1 ~ x
ln (1 + x) ~ x (1 + x)α – 1 ~ α x. При
вычислении пределов функций можно
использовать понятие эквивалентности.
Определение: Пусть a -
предельная точка области определения f(x).
Говорят, что функция f(x)
удовл. в точке a условию
Коши, если ∀
ε > 0 ∃
δ > 0, ∀ x'
и x'',
0 <x'
- a
< δ, 0 <x''- a
< δ: f(x')
- f(x'')
< ε. Условие
Коши для функции аналогично условию
фундаментальности последовательности. Теорема
6.6. (Критерий
Коши)
Для того, чтобы функция имела предел в
точке a,
необходимо и достаточно, чтобы она
удовлетворяла в этой точке условию
Коши. Доказательство. Необходимость.
Дано: ∃ f(x)
= b.
Требуется доказать: f(x)
удовлетворяет в точке a условию
Коши. Зададим произвольное ε > 0.
Согласно определению предела функции
по Коши, ∃
δ
> 0, ∀ x'
∈
{0 <x'
- a
< δ}, f(x')
- b
< , и ∃
δ
> 0, ∀ x''
∈
{0 <x''
- a
< δ}, f(x'')
- b
< . Отсюда
следует, что ∀ x'
∈
{0 <x'
- a
< δ} и ∀ x''
∈
{0 <x''
- a
< δ}: f(x')
- f(x'') = =
( f(x')
- b)
- (f(x'')
- b)≤
+ < ε. А
это и означает, что f(x)
удовлетворяет в точке a условию
Коши. Необходимость
доказана. Достаточность. Дано: f(x)
удовлетворяет в точке a условию
Коши. Требуется доказать: ∃ f(x).
Согласно определению предела функции
по Гейне, нужно доказать, что ∀
{xn}
→ a (xn ≠ a)
{f(xn)}
сход., причем сходится к одному и тому
же числу для всех {xn}
→ a (xn ≠ a).
Рассмотрим произвольную последовательность
{xn}
→ a (xn ≠ a).
Докажем сначала, что последовательность
{f(xn)}
- фундаментальная. Зададим произвольное
ε > 0. Согласно условию (1), ∃
δ > 0, ∀ x'
иx'',
0 <x'
- a
< δ, 0 <x''- a
< δ: f(x')
- f(x'')
< ε. (2). В свою очередь, так как {xn}
→ a и xn ≠ a,
то ∃ N,
∀ n > N:
0 < xn -a<
δ, ∀ m > N:
0 < xm - a<
δ. (3). Из (2) и (3) следует, что ∀ n > N и
∀ m > N:
f(xn)
- f(xm)
< ε. А это и означает по определению,
что последовательность {f(xn)}
- фундаментальная. Следовательно, она
сходится. Итак, мы доказали, что ∀
{xn}
→ a (xn ≠ a):
{f(xn)}
сходится. Остается доказать, что для
всех таких последовательностей {xn}:
{f(xn)}
сходится к одному и тому же числу. Пусть
для {xn}
→ a (xn ≠ a):
{f(xn)}
→ b,
а для {xn'}
→ a (xn' ≠ a):
{f(xn')}
→ b'.
Нужно доказать, чтоb'
= b.
Составим посл. {xn''}
= x1 , x1'
, x2 , x2'
, … , xn , xn''
, … {xn''}
→ a (xn'' ≠ a). Согласно
доказанному, {f(xn'')}
→ b'',
но {f(xn)}
и {f(xn')}
- подпоследовательности последовательности
{f(xn'')},
следовательно, эти последовательности
сходятся к b'',
а это и означает, что b = b'
= b'',
что и требовалось доказать.
Число
Число
называется левым
пределом функции
в
точке
,
если для
такое,
что для любого
и
Левый
и правый пределы функции
называются односторонними
пределами.
Теорема
Если
существуют
В
случае, если
Пример
Задание. Найти
односторонние пределы
функции
Решение. Правый
предел:
Левый
предел:
24.
Арифметические операции над функциями,
имеющими предел.
Теорема
4.2. Пусть
функции
ВВЕДЕНИЕ
Определение
предела. Число b – предел
функции f(x) при x стремящемся
к a,
если для каждого положительного
числа можно
указать такое положительной число ,
что для всех x,
отличных от a и
удовлетворяющих неравенству |x-a|<,
имеет место неравенство |f(x)-b|< Обозначение
предела. Если b есть
предел функции f(x) при x стремящемся
к a,
то записывают это так:
Определение
непрерывной функции. Функция f(x) непрерывна в
точке a,
если
Вычисление
пределов функций основано на применении
следующих основных теорем:
ТЕОРЕМА
1. Предел
суммы двух функций при x стремящемся
к a равен
сумме пределов этих функций , то есть
ТЕОРЕМА
2. Предел
произведения двух функций при x стремящемся
к a равен
произведению пределов этих функций,
то есть
ТЕОРЕМА
3. Предел
частного двух функций при x стремящемся
к a равен
частному пределов, если предел знаменателя
отличен от нуля, то есть
и
равен плюс (минус) бесконечности, если
предел знаменателя 0, а предел числителя
конечен и отличен от нуля.
ТЕОРЕМА
4. Первый
замечательный предел равен
ТЕОРЕМА
5. Второй
замечательный предел равен
ТЕОРЕМА
6. Всякая
элементарная функция непрерывна в
каждой точке, в которой она определена. перейти к
содержанию
ВЫЧИСЛЕНИЕ
ПРЕДЕЛОВ НА ОСНОВЕ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА Пример
1. Докажем,
что
Пусть задано произвольное Тогда
для того чтобы выполнялось неравенство |f(x)-a|<,
необходимо выполнение
неравенства |x-a|<которое,
очевидно, выполняется, если |x-a|<,
где Таким
образом, согласно определению
предела функции,
число a,
действительно, является пределом
функции x при x стремящемся
к a. Пример
2. Докажем,
что
Нужно
доказать, что при произвольном найдется
такое положительное ,
что неравенство
будет
выполняться, если |x-1|<Но,
если x не
равно 1, то (1) эквивалентно неравенству
или
При
произвольном неравенство
(1) будет выполняться, если будет
справедливо (2), а последнее справедливо,
если |x-1|<,
где Поэтому
в соответствии сопределением
предела функции данная
функция при xстремящемся
к 1 имеет пределом число 2. перейти к
содержанию
ВЫЧИСЛЕНИЕ
НЕСЛОЖНЫХ ПРЕДЕЛОВ Пример
1. Комментарий.
Здесь была использована теорема
о пределе суммы. Пример
2. Комментарий.
На первом шаге была применена теорема
о пределе частного,
так как предел знаменателя не равен
нулю. На втором шаге использовалась теорема
о пределе суммы для
числителя и знаменателя дроби. После
была применена теорема
о пределе произведения. Пример
3. Найти
предел
Знаменатель
и числитель дроби при x стремящемся
к 2 стремятся к нулю, поэтому теорема
о пределе частного здесь
неприменима. В таких случаях нужно
попытаться упростить дробь. Имеем
Это
преобразование справедливо при всех
значениях x,
отличных от 2, поэтому в соответствии
с определением предела можем написать перейти к
содержанию
ВЫЧИСЛЕНИЕ
ПРЕДЕЛОВ С ПОМОЩЬЮ ТЕОРЕМЫ О ПЕРВОМ
ЗАМЕЧАТЕЛЬНОМ ПРЕДЕЛЕ Пример
1. Комментарий. На
первом этапе мы раскрыли функцию tg(x) и
представили дробь в виде произведения
дробей. Второй этап связан с
применением теоремы
о пределе произведения.
Первый предел известен,
для нахождения второго используем теорему
о пределе частного.
Наконец, cos(x)
– элементарная функция, поэтому она
непрерына, то есть предел этой функции
равен значению функции в соответствующей
точке. перейти к
содержанию
ВЫЧИСЛЕНИЕ
ПРЕДЕЛОВ С ПОМОЩЬЮ ТЕОРЕМЫ О ВТОРОМ
ЗАМЕЧАТЕЛЬНОМ ПРЕДЕЛЕ Пример
1. Комментарий. Вначале
мы разложили выражение под пределом
на множители, после применили теорему
о пределе произведения.
Пределы второго и третьего сомножителей
равны e. Для
нахождения предела первого сомножителя
используем теорему
о пределе суммы.
Наконец, предел 1/x при x стремящемся
к бесконечности равен 0, так как числитель
дроби ограничен, а знаменатель
неограниченно возрастает.
Продолжаем
наш разговор на тему Пределы
и способы их решения.
Перед изучением материалов данной
страницы настоятельно рекомендую
ознакомиться со статьей Пределы.
Примеры решений.
Из вышеуказанной статьи Вы сможете
узнать, что же такое предел, и с чем его
едят – это ОЧЕНЬ важно. Почему? Можно
не понимать, что такое определители и
успешно их решать, можно совершенно не
понимать, что такое производная и
находить их на «пятёрку». Но вот если
Вы не понимаете, что такое предел, то с
решением практических заданий придется
туго. Также не лишним будет ознакомиться
с образцами оформления решений и моими
рекомендациями по оформлению. Вся
информация изложена в простой и доступной
форме.
А для целей
данного урока нам потребуются следующие
методические материалы:Замечательные
пределы и Тригонометрические
формулы.
Их можно найти на страницеМатематические
формулы, таблицы и справочные материалы.
Лучше всего методички распечатать –
это значительно удобнее, к тому же к
ним часто придется обращаться в оффлайне.
Чем же замечательны
замечательные пределы? Замечательность
данных пределов состоит в том, что они
доказаны величайшими умами знаменитых
математиков, и благодарным потомкам
не приходиться мучаться страшными
пределами с нагромождением
тригонометрических функций, логарифмов,
степеней. То есть при нахождении пределов
мы будем пользоваться готовыми
результатами, которые доказаны
теоретически.
Замечательных
пределов существует несколько, но на
практике у студентов-заочников в 95%
случаев фигурируют два замечательных
предела: Первый
замечательный предел,Второй
замечательный предел.
Следует отметить, что это исторически
сложившиеся названия, и, когда, например,
говорят о «первом замечательном
пределе», то подразумевают под этим
вполне определенную вещь, а не какой-то
случайный, взятый с потолка предел.
Начнем.
Рассмотрим
следующий предел:
Согласно
нашему правилу нахождения пределов
(см. статью Пределы.
Примеры решений)
пробуем подставить ноль в функцию: в
числителе у нас получается ноль (синус
нуля равен нулю), в знаменателе, очевидно,
тоже ноль. Таким образом, мы сталкиваемся
с неопределенностью вида
Данный
математический факт носит название Первого
замечательного предела.
Аналитическое доказательство предела
приводить не буду, а вот его геометрический
смысл рассмотрим на уроке о бесконечно
малых функциях.
Нередко в практических
заданиях функции могут быть расположены
по-другому, это ничего не меняет:
! Но
самостоятельно переставлять числитель
и знаменатель нельзя! Если дан предел
в виде
На практике
в качестве параметра
Примеры:
Здесь
А вот следующая запись
– ересь:
Почему?
Потому-что многочлен
Кстати,
вопрос на засыпку, а чему равен предел
На практике
не все так гладко, почти никогда студенту
не предложат решить халявный предел
Переходим к рассмотрению
практических примеров:
Пример 1
Найти
предел
Если мы замечаем в
пределе синус, то это нас сразу должно
наталкивать на мысль о возможности
применения первого замечательного
предела.
Сначала
пробуем подставить 0 в выражение под
знак предела (делаем это мысленно или
на черновике):
Итак, у
нас есть неопределенность вида
,
ее обязательно
указываем в
оформлении решения. Выражение под
знаком предела у нас похоже на первый
замечательный предел, но это не совсем
он, под синусом находится
В подобных
случаях первый замечательный предел
нам нужно организовать самостоятельно,
используя искусственный прием. Ход
рассуждений может быть таким: «под
синусом у нас
,
значит, в знаменателе нам тоже нужно
получить
».
А
делается это очень просто:
То есть, знаменатель
искусственно умножается в данном случае
на 7 и делится на ту же семерку. Теперь
запись у нас приняла знакомые
очертания.
Когда задание оформляется
от руки, то первый замечательный предел
желательно пометить простым карандашом:
Готово.
Окончательный ответ:
Если не хочется
использовать пометки карандашом, то
решение можно оформить так:
“
Пример 2
Найти
предел
Опять мы
видим в пределе дробь и синус. Пробуем
подставить в числитель и знаменатель
ноль:
Действительно,
у нас неопределенность
и,
значит, нужно попытаться организовать
первый замечательный предел. На
уроке Пределы.
Примеры решений мы
рассматривали правило, что когда у нас
есть неопределенность
,
то нужно разложить числитель и знаменатель
на множители. Здесь – то же самое,
степени мы представим в виде произведения
(множителей):
Далее, по
уже знакомой схеме организовываем
первые замечательные пределы. Под
синусами у нас
Аналогично предыдущему
примеру, обводим карандашом замечательные
пределы (здесь их два), и указываем, что
они стремятся к единице:
Собственно, ответ
готов:
В следующих примерах,
я не буду заниматься художествами в
Пэйнте, думаю, как правильно оформлять
решение в тетради – Вам уже понятно.
Пример 3
Найти
предел
Подставляем ноль в
выражение под знаком передела:
Получена
неопределенность
,
которую нужно раскрывать. Если в пределе
есть тангенс, то почти всегда его
превращают в синус и косинус по известной
тригонометрической формуле
В данном случае:
Косинус нуля равен
единице, и от него легко избавиться (не
забываем пометить, что он стремится к
единице):
Таким образом, если в
пределе косинус является МНОЖИТЕЛЕМ,
то его, грубо говоря, нужно превратить
в единицу, которая исчезает в произведении.
Дальше по накатанной
схеме, организуем первый замечательный
предел:
Здесь все вышло проще,
без всяких домножений и делений. Первый
замечательный предел тоже превращается
в единицу и исчезает в произведении:
В итоге получена
бесконечность, бывает и такое.
Пример 4
Найти
предел
Пробуем подставить
ноль в числитель и знаменатель:
Получена
неопределенность
(косинус
нуля, как мы помним, равен единице)
Используем
тригонометрическую формулу
Постоянные множители
вынесем за значок предела:
Организуем первый
замечательный предел:
Избавимся от
трехэтажности:
Предел фактически
решен, указываем, что оставшийся синус
стремится к нулю:
Пример 5
Найти
предел
Этот пример сложнее,
попробуйте разобраться самостоятельно:
Некоторые
пределы можно свести к 1-ому замечательному
пределу путём замены переменной, об
этом можно прочитать чуть позже в
статье Методы
решения пределов.
В теории математического
анализа доказано, что:
Данный
факт носит название второго
замечательного предела.
Справка:
В качестве
параметра
может
выступать не только переменная
,
но и сложная функция.Важно
лишь, чтобы она стремилась к бесконечности.
Пример 6
Найти
предел
Когда выражение под
знаком предела находится в степени –
это первый признак того, что нужно
попытаться применить второй замечательный
предел.
Но сначала,
как всегда, пробуем подставить бесконечно
большое число в выражение
Нетрудно
заметить, что при
Данная
неопределенность как раз и раскрывается
с помощью второго замечательного
предела. Но, как часто бывает, второй
замечательный предел не лежит на
блюдечке с голубой каемочкой, и его
нужно искусственно организовать.
Рассуждать можно следующим образом: в
данном примере параметр
Когда задание оформляется
от руки, карандашом помечаем:
При
этом сам значок предела перемещаем в
показатель:
Далее, отметки карандашом
я не делаю, принцип оформления, думаю,
понятен.
Пример 7
Найти
предел
Внимание!
Предел подобного типа встречается
очень часто, пожалуйста, очень внимательно
изучите данный пример.
Пробуем подставить
бесконечно большое число в выражение,
стоящее под знаком предела:
В результате
получена неопределенность
Теперь можно почленно
разделить числитель на знаменатель:
Вроде бы
основание стало напоминать
Таким
образом, основание приняло вид
,
и, более того, появилась нужная нам
неопределенность
.
Организуем второй замечательный
предел
Наконец-то
долгожданное
Но на этом
мучения не закончены, в показателе у
нас появилась неопределенность вида
Готово.
А сейчас
мы рассмотрим модификацию второго
замечательного предела. Напомню, что
второй замечательный предел выглядит
следующим образом:
.
Однако на практике время от времени
можно встретить его «перевёртыш»,
который в общем виде записывается так:
Пример 8
Найти
предел
Сначала (мысленно или
на черновике) пробуем подставить ноль
(бесконечно малое число) в выражение,
стоящее под знаком предела:
В результате
получена знакомая неопределенность
.
Очевидно, что в данном примере
Выражение
Еще не
всё, в показателе у нас появилась
неопределенность вида
Косинус нуля стремится
к единице (не забываем помечать
карандашом), поэтому он просто пропадает
в произведении:
А что
такое
и
к чему оно стремится, нужно уже знать,
иначе «двойка»!
Как видите, в практических
заданиях на вычисление пределов нередко
требуется применять сразу несколько
правил и приемов.
Чтобы
окончательно разобраться в пределах
функций, и во 2-ом замечательном пределе
в частности, настоятельно рекомендую
ознакомиться с третьим уроком – Методы
решения пределов.
В 90-95% на
зачете, экзамене Вам встретится первый
замечательный предел или второй
замечательный предел. Как быть, если
попался «экзотический» замечательный
предел? (со списком всех замечательных
пределов можно ознакомиться в
соответствующей методичке). Ничего
страшного, практически все приёмы
решения 1-го замечательного предела
работают и для остальных замечательных
пределов, читайте 2-ой параграф
заключительной статьиСложные
пределы.
Да, так
чему же равен предел
?
Если у Вас
получился ответ
БЕСКОНЕЧНО
МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА Функция y=f(x) называется бесконечно
малой при x→a или
при x→∞,
если П
Функция f(x)=(x-1)2 является
бесконечно малой при x→1,
так как
Функция f(x) =
tgx –
бесконечно малая при x→0.
f(x) =
ln (1+x)–
бесконечно малая при x→0.
f(x) =
1/x–
бесконечно малая при x→∞. Установим
следующее важное соотношение: Теорема. Если
функция y=f(x) представима
при x→aв
виде суммы постоянного числа b и
бесконечно малой величины α(x):
f (x)=b+ α(x) то Обратно,
если
,
то f
(x)=b+α(x),
где a(x) –
бесконечно малая при x→a. Доказательство.
Докажем
первую часть утверждения. Из
равенства f(x)=b+α(x) следует |f(x)
– b|=| α|.
Но так как a(x) –
бесконечно малая, то при произвольном
ε найдется δ – окрестность точки a,при
всех x из
которой, значения a(x) удовлетворяют
соотношению |α(x)|<ε.
Тогда |f(x)
– b|< ε.
А это и значит, что
.
Если
,
то при любом ε>0 для
всех х из
некоторой δ – окрестность
точки a будет |f(x)
– b|< ε.
Но если обозначимf(x)
– b= α,
то |α(x)|<ε,
а это значит, что a –
бесконечно малая. Рассмотрим
основные свойства бесконечно малых
функций. Теорема
1. Алгебраическая
сумма двух, трех и вообще любого конечного
числа бесконечно малых есть функция
бесконечно малая. Доказательство.
Приведем доказательство для двух
слагаемых. Пусть f(x)=α(x)+β(x),
где Итак,
зафиксируем произвольное число ε>0.
Так как по условию теоремы α(x) –
бесконечно малая функция, то найдется
такое δ1>0,
что при |x
– a|<δ1 имеем |α(x)|< ε/2. Аналогично,
так как β(x) –
бесконечно малая, то найдется такое
δ2>0,
что при |x
– a|<δ2 имеем |
β(x)|< ε/2. Возьмем δ=min{ δ1, δ2}.Тогда
в окрестности точки a радиуса δбудет
выполняться каждое из неравенств |α(x)|< ε/2
и |
β(x)|< ε/2. Следовательно,
в этой окрестности будет |f(x)|=|
α(x)+β(x)|
≤ |α(x)|
+ | β(x)| < ε/2
+ ε/2= ε, т.е. |f(x)|<ε,
что и требовалось доказать. Теорема
2. Произведение
бесконечно малой функции a(x) на
ограниченную функцию f(x) при x→a (или
при x→∞)
есть бесконечно малая функция. Доказательство.
Так как функция f(x) ограничена,
то существует число М такое,
что при всех значениях x из
некоторой окрестности точки a|f(x)|≤M. Кроме
того, так как a(x) –
бесконечно малая функция при x→a,
то для произвольного ε>0
найдется окрестность точки a,
в которой будет выполняться
неравенство |α(x)|< ε/M.
Тогда в меньшей из этих окрестностей
имеем |
αf|< ε/M=
ε. А это и значит, что af –
бесконечно малая. Для случая x→∞ доказательство
проводится аналогично. Из
доказанной теоремы вытекают: Следствие
1. Если
и
,
то Следствие
2. Если
и c=const,
то Теорема
3. Отношение
бесконечно малой функции α(x) на
функцию f(x),
предел которой отличен от нуля, есть
бесконечно малая функция. Доказательство.
Пусть
СООТНОШЕНИЕ
МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И
БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ Теорема
1. Если
функция f(x) является
бесконечно большой при x→a,
то функция 1/f(x) является
бесконечно малой при x→a. Доказательство. Возьмем
произвольное число ε>0 и
покажем, что при некотором δ>0 (зависящим
от ε) при всех x,
для которых |x
– a|<δ,
выполняется неравенство Примеры.
Ясно,
что при x→+∞ функция y=x2+1
является бесконечно большой. Но тогда
согласно сформулированной выше теореме
функция
Можно
доказать и обратную теорему. Теорема
2. Если
функция f(x) -
бесконечно малая при x→a (или x→∞) и
не обращается в нуль, то y=1/f(x) является
бесконечно большой функцией. Доказательство
теоремы проведите самостоятельно. Примеры.
Таким
образом, простейшие свойства бесконечно
малых и бесконечно больших функций
можно записать с помощью следующих
условных соотношений: A≠
0
ТЕОРЕМЫ
О ПРЕДЕЛАХ Теорема
1. Предел
алгебраической суммы двух, трех и вообще
определенного числа функций равен
алгебраической сумме пределов этих
функций, т.е.
Доказательство.
Проведем доказательство для двух
слагаемых, так как для любого числа
слагаемых оно проводится так же.
Пусть
f(x)
+ g(x)=(b + c) + (α(x) + β(x)). Так
как b
+ cесть
постоянная величина, а α(x)
+ β(x) –
функция бесконечно малая, то
Пример. Теорема
2. Предел
произведения двух, трех и вообще
конечного числа функций равен произведению
пределов этих функций: Доказательство.
Пусть
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и fg
= (b + α)(c + β) = bc + (bβ + cα + αβ). Произведение bc есть
величина постоянная. Функция bβ
+ c α + αβ на
основании свойств бесконечно малых
функций есть величина бесконечно малая.
Поэтому Следствие
1. Постоянный
множитель можно выносить за знак
предела:
Следствие
2. Предел
степени равен степени предела:
Пример. Теорема
3. Предел
частного двух функций равен частному
пределов этих функций, если предел
знаменателя отличен от нуля, т.е.
Доказательство.
Пусть
Дробь Примеры.
Рассмотрим Т Смысл
этой теоремы понятен из рисунка. Доказательство
теоремы 4 можно найти, например, в
учебнике: Пискунов Н. С. Дифференциальное
и интегральное исчисления, т. 1 – М.:
Наука, 1985. Теорема
5. Если
при x→a (или x→∞)
функция y=f(x) принимает
неотрицательные значения y≥0 и
при этом стремится к пределу b,
то этот предел не может быть
отрицательным: b≥0. Доказательство.
Доказательство проведем методом от
противного. Предположим, что b<0,
тогда |y
– b|≥|b| и,
следовательно, модуль разности не
стремится к нулю при x→a.
Но тогда y не
стремится к пределу b при x→a,
что противоречит условию теоремы. Теорема
6. Если
две функции f(x) и g(x) при
всех значениях аргумента x удовлетворяют
неравенству f(x)≥
g(x) и
имеют пределы Доказательство. По
условию теоремы f(x)-g(x)
≥0,
следовательно, по теореме 5
ОДНОСТОРОННИЕ
ПРЕДЕЛЫ Д Если f(x) стремится
к пределу b при x стремящемся
к некоторому числу a так,
что xпринимает
только значения, меньшие a,
то пишут Таким
образом, число b называется
пределом функции y=f(x) при x→aслева,
если каково бы ни было положительное
число ε, найдется такое число δ (меньшееa),
что для всех Аналогично,
если x→a и
принимает значения большие a,
то пишут Заметим,
что если пределы слева и справа в
точке a для
функции f(x) не
совпадают, то функция не имеет предела
(двустороннего) в точке а. Примеры.
Р
Найдем
пределы функции f(x) при x→3.
Очевидно,
ТИПЫ
НЕОПРЕДЕЛЕННОСТЕЙ И
СПОСОБЫ ИХ РАСКРЫТИЯ Часто
при вычислении пределов какой-либо
функции, непосредственное применение
теорем о пределах не приводит к желаемой
цели. Так, например, нельзя применять
теорему о пределе дроби, если ее
знаменатель стремится к нулю. Поэтому
часто прежде, чем применять эти теоремы,
необходимо тождественно преобразовать
функцию, предел которой мы ищем. Условные
выражения
характеризуют
типы неопределенностей и применяются
для обозначения переменных величин,
при вычислении предела которых нельзя
сразу применять общие свойства пределов. Рассмотрим
некоторые приемы раскрытия
неопределенностей. I. Неопределенность
.
При
разложении числителя на множители
воспользовались правилом деления
многочлена на многочлен «углом». Так
как число x=1
является корнем многочлена x3 –
6x2 +
11x–
6, то при делении получим
II. Неопределенность
При
вычислении предела числитель и
знаменатель данной дроби разделили
на x в
старшей степени.
При
вычислении предела воспользовались
равенством Следующие
виды неопределенностей с помощью
алгебраических преобразований функции,
стоящей под знаком предела, сводят к
одному из рассмотренных выше
случаев
или
. III. Неопределенность
0 ·∞. IV. Неопределенность
∞ –∞.
Мы повторим
здесь определение непрерывности
функции, данное выше, в главе о пределах.
Определение 3.1
Пусть функция
Пусть
функция
определена
на некотором полуинтервале
Пусть,
наконец, функция
определена
на некотором полуинтервале
Из теоремы о
связи двустороннего предела с
односторонними (теорема 2.1) сразу
следует, как уже отмечалось в главе 2,
что имеет место следующее предложение.
Предложение 3.1 Функция
тогда
и только тогда непрерывна в точке
,
когда она непрерывна в точке
справа
и слева, то есть когда выполнены следующие
условия: 1)
функция
определена
в точке
и
в некоторой окрестности этой точки; 2)
существует предел значений функции
слева: 3)
существует предел значений функции
справа: 4)
эти два предела совпадают между собой
и со значением функции в точке
:
Рис.3.1.Функция
непрерывна: пределы слева и справа
совпадают с
Точка
,
в которой функция непрерывна,
называется точкой
непрерывности функции
;
так же определяются точки непрерывности
слева и справа.
Пример 3.1
Пусть (Функция
Пример 3.2
Рассмотрим функцию Тем, кто
внимательно изучил данное в главе 2
общее понятие базы предела, можно
предложить продумать и доказать
следующее утверждение:
Предложение 3.2 Пусть
СЛОЖНАЯ
ФУНКЦИЯ
- функция,
представленная как композиция нескольких
функций. Если множество значений Yi функции fi содержится
во множестве определения Х i+1 функции fi+1,
т. е.
то
функция
наз.
сложной функцией или (п-1)-кратной
композицией (суперпозицией) функций f1, f2,
. . ., fn.
Напр., всякая рациональная
функция любого
числа переменных является композицией
четырех арифметич. действий, т. е.
композицией функций х+у,
x-у, ху, х/у.
С.
ф. сохраняет многие свойства функций,
композицией к-рых она является. Так,
композиция непрерывных функций
непрерывна. Это означает, что если
функция
Понятие
композиции функций представляет собой
наиболее широкое понимание термина
"представление функции формулой".
Задача о представлении функций в виде
композиций возникла в связи с отысканием
формул для решений алгебраич. уравнений.
Всякий кореньуравнения
степени не выше четвертой может быть
представлен формулой, выражающей его
через коэффициенты уравнения и
представляющей собой композицию четырех
арифметич. действий и радикалов.
Всякое уравнение степени
Таким
образом, каждый корень уравнения
степени
через
коэффициенты х,
у и
z этого уравнения посредством композиций
каких-либо непрерывных функций двух
переменных (следует отметить, что всякая
функция конечного числа переменных
является композицией разрывных функций
двух переменных). Д. Гильбертом была
показана невозможность получения всех
аналитич. ций трех переменных в виде
композиций аналитич. ций двух переменных.
Он же для уравнения 9-й степени доказал
[5], что решение уравнения
9-й степени можно представить в виде
композиции алгебраич. функций четырех
переменных (вместо пяти, как это сразу
следует из применения преобразования
Чирнгаузена). Эти исследования были
продолжены многими математиками (см.
[6] - [19]).
А.
Г. Витушкин в 1954 доказал [10], что если
натуральные числа m,
п, m1 и n1 удовлетворяют
неравенству
В
1956 А. Н. Колмогоров показал [11], что всякая
определенная на n-мерном (
Этот цикл работ
завершает следующая теорема Колмогорова
[13]: любая непрерывная функция гс
переменных может быть получена с помощью
композиций непрерывных функций одного
переменного и единственной функции
двух неременных g(x,
y) =
x+y;именно,
он доказал, что любая функция f, непрерывная
на n-мерном кубе, может быть представлена
в виде
где
функции hi и
jij-
непрерывны, а функции jij,
кроме того, стандартны, т. е. не зависят
от выбора функции f.
А.
Г. Витушкин показал [14], что для любых
конечных наборов непрерывных функций pk и
непрерывно дифференцируемых
функций qk,зависящих
от ппеременных, k=1, 2, ..., т,
n=1,
2, ..., существуют даже аналитич. ции гс
переменных, не представимые композицией
вида
где fk -
произвольные непрерывные функции
одного переменного.
5.
Свойства функций, непрерывных на
отрезке
След. »
Свойство
1: (Первая
теорема Вейерштрасса (Вейерштрасс
Карл (1815-1897) - немецкий математик)).
Функция, непрерывная на отрезке,
ограничена на этом отрезке, т.е. на
отрезке
Доказательство
этого свойства основано на том, что
функция, непрерывная в точке
Свойство
2: Функция,
непрерывная на отрезке
,
принимает на нем наибольшее и наименьшее
значения.
Т.е.
существуют такие значения
Отметим
эти наибольшие и наименьшие значения
функция может принимать на отрезке
и несколько раз (например -
Разность
между наибольшим и наименьшим значением
функции на отрезке называется
колебанием функции
на отрезке.
Свойство
3: (Вторая
теорема Больцано - Коши). Функция,
непрерывная на отрезке
,
принимает на этом отрезке все значения
между двумя произвольными величинами.
Свойство
4:
Если функция
Свойство
5:
(Первая теорема Больцано (1781-1848) -
Коши). Если функция
-
непрерывная на отрезке
и
имеет на концах отрезка значения
противоположных знаков, то существует
такая точка внутри этого отрезка,
где
Т.е.
если
Определение. Функция
называется равномерно
непрерывной на отрезке
,
если для любого
Отличие
равномерной непрерывности от “обычной”
в том, что для любого существует
свое
Свойство
6: Теорема
Кантора (Кантор Георг (1845-1918) - немецкий
математик). Функция, непрерывная на
отрезке, равномерно непрерывна на
нем. (Это свойство справедливо только
для отрезков, а не для интервалов и
полуинтервалов.)
Свойство
7:
Если функция
определена,
монотонна и непрерывна на некотором
промежутке, то и обратная ей
функция
Пример. Исследовать
на непрерывность функцию и определить
тип точек разрыва, если они есть.
точка
разрыва 1 - го рода
<<
Предыдушая
Следующая
>>
Р.
Аллен. МАТЕМАТИЧЕСКАЯ ЭКОНОМИЯ, 1963 -
перейти к содержанию учебника
5.8.
НЕПРЕРЫВНЫЕ РЕШЕНИЯ РАЗНОСТНЫХ
УРАВНЕНИЙ
Разностное
уравнение относительно Yx относится
к любому ряду равноотстоящих
(equally-spaced) значений независимой
переменной х. Рассмотренные до сих
пор дискретные решения применимы к
одному частному ряду значений
переменной х = 0, 1, 2, 3, ... Однако разностное
уравнение не ограничивается таким
путем; отправной точкой для х может
быть любое значение. Если отправной
точкой является х = 0, то разностное
уравнение порождает дискретное
решение У0, Yx, У2, •••• Если в качестве
начальной 1 точки
выбрать х = , то получится совершенно
отличное дискретное решение Уі/2,
Уз/2, Г5/2. Очевидно, что не существует
ограничений для того, чтобы получить
какое угодно число различных дискретных
решений. Можно выбрать любое значение
х между 0 и 1 в качестве начальной
точки, и х можно заставить изменяться
непрерывно. Спрашивается, можно ли
все дискретные решения объединить в
отдельное непрерывное решение,
выражающее Yx в виде функции х, вообще
для любого ряда равноотстоящих
значений х. Например,
предположим, что разностное уравнение
характеризует уровень цен Yx в различные
моменты времени х, а интервал значений
х равен одному году. В этом случае х
= 0, 1, 2, ... может означать, например,
конец года, и дискретное решение У
будет тогда показывать изменение цен
на 13
5 конец
года от года к году. Но если положить
х — y ' ~2 ' 2~' т0 П°ЛУЧИТСЯ другое
дискретное решение Ух, которое будет
показывать годовое изменение цен, но
только на середину года. В обоих этих
случаях, так же как и в других, подобных
им, изменение цен в пределах года
(например, сезонные колебания цен) в
анализе не учитывается. Проблема
сводится к тому, можно ли получить
непрерывное решение для Yx, которое
характеризовало бы полностью изменение
цен во времени, то есть не только
изменение цен год от года, но и изменение
их в пределах каждого года. Уравнение
первого порядка %(х, Yx, Ух-1) = 0 имеет
дискретное решение Yx — Y(x\ Л), содержащее
одну произвольную постоянную А. Какой
бы частный ряд значений х мы ни
рассматривали, А всегда можно выразить
через начальное значение У.
Если
дано У0, решение относится к Yx при я =
0, 1, 2, ...; если начальное значение задано
Уі/2, то ре- V
13 5 шение
относится к Ух при я = у, у, ... и так
далее для всех задаваемых Yx при х в
"интервале 0<я<1. Теперь мы расширим
понятие произвольного элемента;
вместо одного заданного Ух, например
У0 или Уі/2, мы будем рассматривать
целую область задаваемых Yx при 0<я<1.
Говоря более точно, вместо одной
произвольной начальной величины, мы
возьмем произвольную начальную
функцию в области 0<я<1. Эта функция
может начинаться с любого значения
У0 и изменяться любым способом от х =
0 до х=\, возвращаясь при ж = 1 к начальному
значению. Наша произвольная функция
имеет период 1. Если продолжить наш
пример с ценами, где Yx характеризует
уровень цен, то произвольный элемент,
который мы должны указать,— это вся
область цен в пределах года, выраженных
в форме сезонных изменений, начинающихся
и кончающихся на одном и том же уровне.
Если это сделано, разностное уравнение
дает Yx для любых значений х, изменяющихся
непрерывно. Обозначим
через w(x) любую функцию с периодом 1,
так что все значения w, разделенные
единичным интервалом х, равны.
Следовательно, для единичного интервала
= Так же как и производная постоянной,
разность функций периода 1 равна нулю.
Постоянная исчезает при дифференцировании,
функция периода 1 исчезает при
исчислении дифференцирования по
конечной разности. Таким образом,
общее непрерывное решение уравнения
% (х, Ух, Yx_t) = 0 имеет вид Yx = У (х{, w), где
w — произвольная функция периода 1,
которая может быть определена через
начальные условия для Ух в интервале
0<ж< 1. Понятие непрерывного решения
легко обобщить. Разностное уравнение
второго порядка %(х, Yx, Yx_±, Yx_2) =0 имеет
дискретное решение Yx = Y(x; Av А2) при ж =
0, 1, 2, ..., где Аг и А2 — произвольные
постоянные, которые можно отождествить
с У0 и Уг Это же уравнение имеет
непрерывное решение Yx = Y(x; ОУ2) для
любого х, где и ^ — произвольные функции
периода 1, которые можно выразить
через начальные условия для Yx в двух
интервалах 0<я<1 и 1<#<2.
Очевидно,
это можно обобщить для разностного
уравнения любого порядка. Все, что
раньше было сказано о произвольных
постоянных или начальных значениях
в дискретном решении, в равной степени
относится и к произвольным функциям
периода 1 в непрерывном решении. Решения
разностных и дифференциальных
уравнений имеют ряд отличающих их
друг от друга черт. Например, область
возможных решений линейных разностных
уравнений (зависящих от показательной
функции типа ах) вообще значительно
шире или богаче, чем для линейных
дифференциальных уравнений, решения
которых зависят от показательной
функции типа еах. Это ясно из нашего
анализа в разделах 5.3 — 5.5. Однако
сравнение, настоящей и предыдущей
глав показывает, что методы решения
линейных дифференциальных и разностных
уравнений имеют очень много общего,
хотя они в значительно большей степени
освоены и разработаны для дифференциальных
уравнений. Наконец,
отметим, что разностные уравнения
можно решать методами, аналогичными
преобразованию Лапласа для
дифференциальных уравнений (см. 4.7).
Если положить YX = Y0 во всем интервале
0<#< 1, то частное дискретное решение
Yx(x = 0, 1, 2,...) превращается в частное
непрерывное решение. Это решение
становится в таком случае ступенчатой
функцией непрерывной переменной: Y(x)
= Y0 (0<а<1); =УХ (1<я<2);..., и
можно' применить метод преобразования
Лапласа [4]. Альтернативно для дискретного
ряда Yx преобразование можно определить
через суммы — аналогично интегралу
преобразования Лапласа для функции
непрерывной переменной. Простым
преобразованием такого типа является
функция женератриса (generating function)32: со
х=0 в
которой коэффициенты при возрастающих
степенях s образуют последовательность
значений Yx. Решение разностных
уравнений преобразованием Yx в У (я)
очень похоже на преобразование Лапласа
в случае дифференциальных уравнений
(см. [5], особенно пример там на стр.
194).
Пусть
функция
как
только
При
изменении
Рис.
29
В
связи с этим естественно выделить те
непрерывные функции, для которых при
данном
можно
указать
,
пригодное сразу для всех
Начнем
с определения.
О
п р е д е л е н и е 1. Функция
,
определенная на множестве
для
всех
Легко
видеть, что если функция равномерно
непрерывна на множестве
,
то тем более она равномерно непрерывна
на любом его подмножестве
Т
е о р е м а 1. Если функция
Д
о к а з а т е л ь с т в о. Допустим, что
теорема неверна. Тогда существует
такое
Зададим
стремящуюся к нулю последовательность
положительных чисел
Так
как последовательности
После
перехода к пределу в (1) при
получим
и
мы пришли к противоречию:
Заметим,
что в (2) мы воспользовались непрерывностью
функции
П
р и м е р 1. Функция
непрерывна
на отрезке
С
другой стороны, на полуинтервале
Убедимся
в том, что наша функция не является
равномерно непрерывной на
.
Точки
Если
задать
между
тем как
Из
сказанного следует, что нашу функцию
нельзя продолжить на отрезок
Точки
разрыва и их классификация.
Рассмотрим
некоторую функцию f(x),
непрерывную в окрестности точки х0,
за исключением может быть самой этой
точки. Из определения точки разрыва
функции следует, что х = х0является
точкой разрыва, если функция не
определена в этой точке, или не является
в ней непрерывной.
Следует
отметить также, что непрерывность
функции может быть односторонней.
Поясним это следующим образом.
Если
односторонний предел (см. выше)

![]() при x → 0.
при x → 0.
![]()
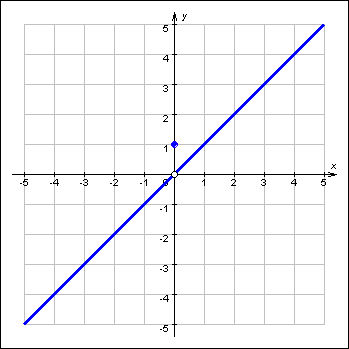
![]() в
точке a = 0 равен
0:
в
точке a = 0 равен
0: 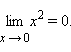 Предел
функции
в
точке a = 0 также
равен 0, хотя эта функция не существует
в этой точке (ее знаменатель обращается
в нуль). Предел функции
Предел
функции
в
точке a = 0 также
равен 0, хотя эта функция не существует
в этой точке (ее знаменатель обращается
в нуль). Предел функции  в
точке a = 0 равен
0, хотя значение функции в этой
точке f (0) = 1.
в
точке a = 0 равен
0, хотя значение функции в этой
точке f (0) = 1.![]() выполняется
неравенство
выполняется
неравенство ![]()
![]() выполняется
неравенство
выполняется
неравенство ![]()
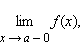 предел
справа –
предел
справа – 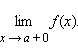 Эти
пределы характеризуют поведение функции
слева и справа от точки a.
Их часто называютодносторонними
пределами.
В обозначении односторонних пределов
при x → 0 обычно
опускают первый нуль:
Эти
пределы характеризуют поведение функции
слева и справа от точки a.
Их часто называютодносторонними
пределами.
В обозначении односторонних пределов
при x → 0 обычно
опускают первый нуль: 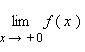 и
и 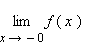 . Так,
для функции
. Так,
для функции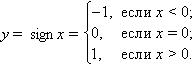
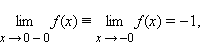
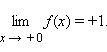
![]()
![]() имеет
в точке x = 0 бесконечный
предел
имеет
в точке x = 0 бесконечный
предел 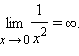 Часто
различают пределы, равные +∞ и –∞.
Так,
Часто
различают пределы, равные +∞ и –∞.
Так, 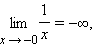
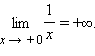
![]()
 В
качестве примера приведем функцию
В
качестве примера приведем функцию ![]() которая
стремится на бесконечности к нулю:
которая
стремится на бесконечности к нулю: 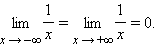
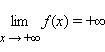 означает,
что для любого ε > 0 существует
такое δ > 0, что для любого x > δ
выполняется неравенство f (x) > ε.
Запись
означает,
что для любого ε > 0 существует
такое δ > 0, что для любого x > δ
выполняется неравенство f (x) > ε.
Запись 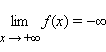 означает,
что для любого ε > 0 существует
такое δ > 0, что для любого x > δ
выполняется неравенство f (x) < –ε.
Запись
означает,
что для любого ε > 0 существует
такое δ > 0, что для любого x > δ
выполняется неравенство f (x) < –ε.
Запись 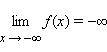 означает,
что для любого ε > 0 существует
такое δ > 0, что для любого x < –δ
выполняется неравенство f (x) < –ε.
означает,
что для любого ε > 0 существует
такое δ > 0, что для любого x < –δ
выполняется неравенство f (x) < –ε.
![]() ,
,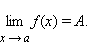
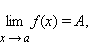
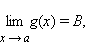 то A ≤ B.
то A ≤ B.
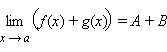 ,
,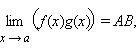
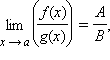 если B ≠ 0 и
если g (x) ≠ 0 в
δ-окрестности точки a.
если B ≠ 0 и
если g (x) ≠ 0 в
δ-окрестности точки a.
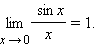
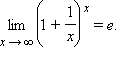
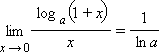
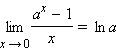
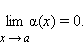 Функция x = 0 является
бесконечно малой функцией в каждой
точке. Примерами бесконечно малых (на
бесконечности) функций являются
зависимость силы тяжести от расстояния
до притягивающего центра или зависимость
скорости движения по параболической
орбите от времени.
Функция x = 0 является
бесконечно малой функцией в каждой
точке. Примерами бесконечно малых (на
бесконечности) функций являются
зависимость силы тяжести от расстояния
до притягивающего центра или зависимость
скорости движения по параболической
орбите от времени.
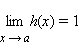 ,
то функции f (x) и g (x) называются эквивалентными при x → a:
,
то функции f (x) и g (x) называются эквивалентными при x → a:
![]() и
и ![]() эквивалентны
при x → 0,
так как
эквивалентны
при x → 0,
так как 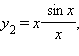 а
второй множитель стремится к 1 при x → 0.
Другие примеры эквивалентных функций
приx → 0:
а
второй множитель стремится к 1 при x → 0.
Другие примеры эквивалентных функций
приx → 0:
Критерий Коши существования предела функции в точке.
![]() называется правым
пределом функции
называется правым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для ![]()
![]() такое,
что для любого
такое,
что для любого ![]() и
и ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() (рис.
1). Правый предел обозначается
(рис.
1). Правый предел обозначается ![]()
![]() ,
выполняется неравенство
(рис.
2). Левый предел обозначается
,
выполняется неравенство
(рис.
2). Левый предел обозначается ![]()
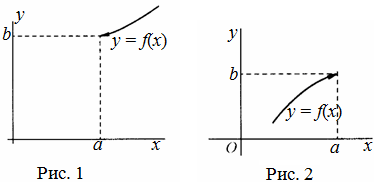
![]() и
и ![]() ,
причем
,
причем ![]() ,
то существует и
,
то существует и ![]() .
Обратное утверждение также верно.
.
Обратное утверждение также верно.![]() ,
то предел
,
то предел ![]() не
существует.
не
существует.![]() при
при ![]()
![]()
![]()
![]() и
и ![]() имеют
в точке
имеют
в точке ![]() пределы
и эти пределы соответственно равны
пределы
и эти пределы соответственно равны ![]() и
и ![]() .
Тогда функции
.
Тогда функции ![]() ,
, ![]() имеют
в точке
пределы,
равные соответственно
имеют
в точке
пределы,
равные соответственно ![]() Если
кроме этого,
Если
кроме этого, ![]() ,
то в точке
существует
предел функции
,
то в точке
существует
предел функции![]() равный
равный ![]() .
Доказательство. Пусть
.
Доказательство. Пусть ![]() -
произвольная сходящаяся к
последовательность
значений аргумента, элементы которой
отличны от
.
Тогда последовательности
-
произвольная сходящаяся к
последовательность
значений аргумента, элементы которой
отличны от
.
Тогда последовательности ![]() и
и ![]() сходятся
соответственно к пределам
и
.
Но тогда, в силу теоремы 3.7,
последовательности
сходятся
соответственно к пределам
и
.
Но тогда, в силу теоремы 3.7,
последовательности
![]() и
и 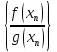 (при
)
имеют пределы, соответственно
равные
(при
)
имеют пределы, соответственно
равные ![]() и
.
Последнее утверждение, в силу определения
предела функции по Гейне, означает,
что
и
.
Последнее утверждение, в силу определения
предела функции по Гейне, означает,
что ![]() ,
, ![]() ,
, 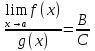 .
Теорема 4.2 доказана.
Теорема
4.3. Пусть
функции
.
Теорема 4.2 доказана.
Теорема
4.3. Пусть
функции ![]() и
и ![]() определены
в некоторой окрестности точки
,
за исключением, быть может, самой
точки
и
имеют в этой точке равные пределы. Пусть
кроме этого выполняются неравенства
определены
в некоторой окрестности точки
,
за исключением, быть может, самой
точки
и
имеют в этой точке равные пределы. Пусть
кроме этого выполняются неравенства ![]() .
Тогда существует
.
Тогда существует ![]() при
этом
при
этом ![]() .
Доказательство. Пусть
.
Доказательство. Пусть ![]() -
произвольная, сходящаяся
к
последовательность,
элементы которой отличны от
.
Тогда соответствующие
последовательности
и
-
произвольная, сходящаяся
к
последовательность,
элементы которой отличны от
.
Тогда соответствующие
последовательности
и ![]() имеют
предел, и эти пределы равны. Из условия
теоремы следует, что
имеют
предел, и эти пределы равны. Из условия
теоремы следует, что ![]() .
Тогда согласно теореме 3.9
.
Тогда согласно теореме 3.9 ![]() Следовательно,
существует и
Следовательно,
существует и ![]() и
при этом
.
Теорема 4.3 доказана.
и
при этом
.
Теорема 4.3 доказана. ![]()
![]()
![]()
![]()
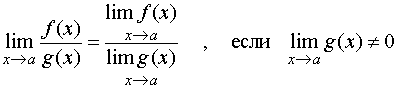
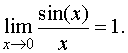
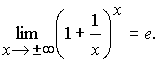
![]()
![]()
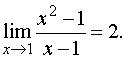

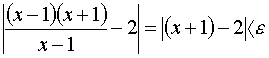
![]()
![]()
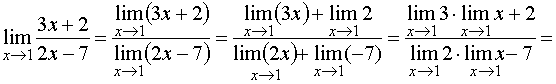
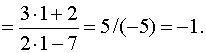
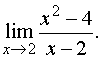
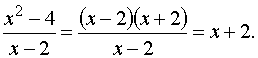
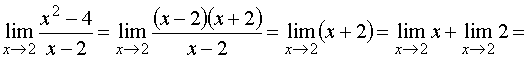
![]()
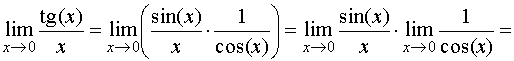
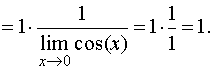
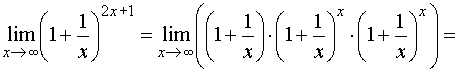
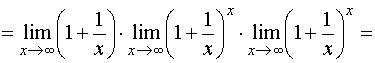
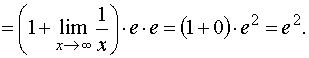
Замечательные пределы. Примеры решений
Первый замечательный предел
![]() (вместо
родной буквы «хэ» я буду использовать
греческую букву «альфа», это удобнее
с точки зрения подачи материала).
(вместо
родной буквы «хэ» я буду использовать
греческую букву «альфа», это удобнее
с точки зрения подачи материала).![]() ,
которую, к счастью, раскрывать не нужно.
В курсе математического анализа,
доказывается, что:
,
которую, к счастью, раскрывать не нужно.
В курсе математического анализа,
доказывается, что:![]()
![]() –
тот
же самый первый замечательный предел.
–
тот
же самый первый замечательный предел.![]() ,
то и решать его нужно в таком же виде,
ничего не переставляя.
,
то и решать его нужно в таком же виде,
ничего не переставляя.![]() может
выступать не только переменная
может
выступать не только переменная ![]() ,
но и элементарная функция, сложная
функция. Важно
лишь, чтобы она стремилась к нулю.
,
но и элементарная функция, сложная
функция. Важно
лишь, чтобы она стремилась к нулю.![]() ,
, 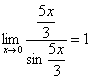 ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
и всё гуд – первый замечательный предел
применим.
,
и всё гуд – первый замечательный предел
применим.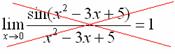
![]() не
стремится к нулю, он стремится к пятерке.
не
стремится к нулю, он стремится к пятерке.![]() ?
Ответ можно найти в конце урока.
?
Ответ можно найти в конце урока.![]() и
получить лёгкий зачет. Хммм… Пишу эти
строки и пришла в голову очень важная
мысль – все-таки «халявные» математические
определения и формулы вроде
и
получить лёгкий зачет. Хммм… Пишу эти
строки и пришла в голову очень важная
мысль – все-таки «халявные» математические
определения и формулы вроде ![]() лучше
помнить наизусть, это может оказать
неоценимую помощь на зачете, когда
вопрос будет решаться между «двойкой»
и «тройкой», и преподаватель решит
задать студенту какой-нибудь простой
вопрос или предложить решить простейший
пример («а может он (а) все-таки знает
чего?!»).
лучше
помнить наизусть, это может оказать
неоценимую помощь на зачете, когда
вопрос будет решаться между «двойкой»
и «тройкой», и преподаватель решит
задать студенту какой-нибудь простой
вопрос или предложить решить простейший
пример («а может он (а) все-таки знает
чего?!»).![]()
![]()
![]() ,
а в знаменателе
,
а в знаменателе ![]() .
.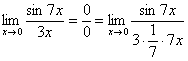
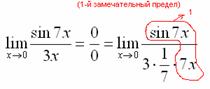 Что
произошло? По сути, обведенное выражение
у нас превратилось в единицу и исчезло
в произведении:
Что
произошло? По сути, обведенное выражение
у нас превратилось в единицу и исчезло
в произведении:
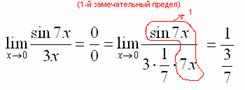 Теперь
только осталось избавиться от
трехэтажности дроби:
Теперь
только осталось избавиться от
трехэтажности дроби:
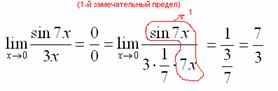 Кто
позабыл упрощение многоэтажных дробей,
пожалуйста, освежите материал в
справочникеГорячие
формулы школьного курса математики.
Кто
позабыл упрощение многоэтажных дробей,
пожалуйста, освежите материал в
справочникеГорячие
формулы школьного курса математики.![]()
![]() Используем
первый замечательный предел
Используем
первый замечательный предел
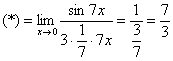 “
“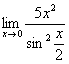
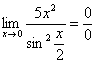
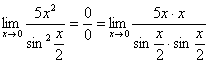
![]() ,
значит, в числителе тоже нужно получить
:
,
значит, в числителе тоже нужно получить
: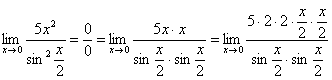
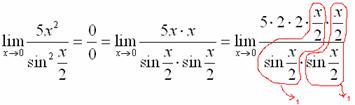
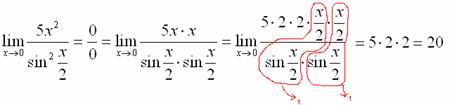
![]()
![]()
![]() (кстати,
с котангенсом делают примерно то же
самое, см. методический материалГорячие
тригонометрические формулы на
странице Математические
формулы, таблицы и справочные материалы).
(кстати,
с котангенсом делают примерно то же
самое, см. методический материалГорячие
тригонометрические формулы на
странице Математические
формулы, таблицы и справочные материалы).![]()
![]()
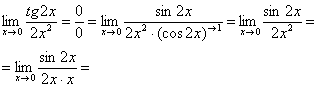
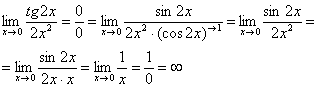
![]()
![]()
![]() .
Возьмите на заметку! Пределы с применением
этой формулы почему-то встречаются
очень часто.
.
Возьмите на заметку! Пределы с применением
этой формулы почему-то встречаются
очень часто.![]()
![]()
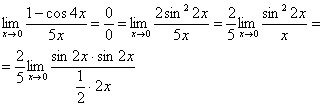 Здесь
у нас только один замечательный предел,
который превращается в единицу и
исчезает в произведении:
Здесь
у нас только один замечательный предел,
который превращается в единицу и
исчезает в произведении: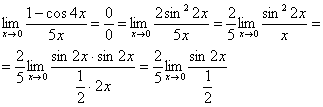
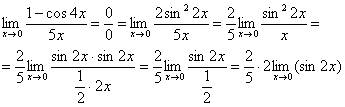
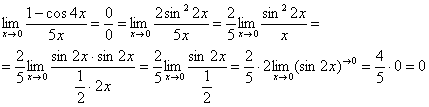
![]()
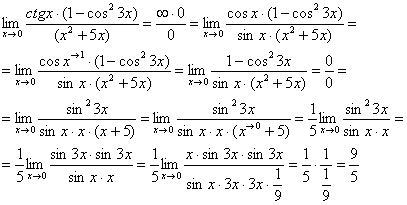
Второй замечательный предел
![]()
![]() –
это иррациональное число.
–
это иррациональное число.![]()
![]() ,
по какому принципу это делается,
разобрано на уроке Пределы.
Примеры решений.
,
по какому принципу это делается,
разобрано на уроке Пределы.
Примеры решений.![]() основание
степени
основание
степени ![]() ,
а показатель –
,
а показатель – ![]() ,
то есть имеется, неопределенность
вида
,
то есть имеется, неопределенность
вида ![]() :
:![]()
![]() ,
значит, в показателе нам тоже нужно
организовать
.
Для этого возводим основание в степень
,
и, чтобы выражение не изменилось –
возводим в степень
,
значит, в показателе нам тоже нужно
организовать
.
Для этого возводим основание в степень
,
и, чтобы выражение не изменилось –
возводим в степень ![]() :
: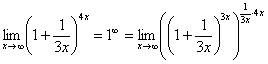
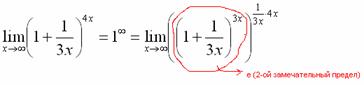 Практически
всё готово, страшная степень превратилась
в симпатичную букву
Практически
всё готово, страшная степень превратилась
в симпатичную букву ![]() :
: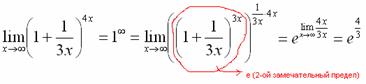
![]()
![]()
![]() .
Но второй замечательный предел применим
к неопределенности вида
.
Что делать? Нужно преобразовать основание
степени. Рассуждаем так: в знаменателе
у нас
.
Но второй замечательный предел применим
к неопределенности вида
.
Что делать? Нужно преобразовать основание
степени. Рассуждаем так: в знаменателе
у нас ![]() ,
значит, в числителе тоже нужно
организовать
:
,
значит, в числителе тоже нужно
организовать
:![]()
![]()
![]() ,
но у нас знак «минус» да и тройка какая-то
вместо единицы. Поможет следующее
ухищрение, делаем
дробь трехэтажной:
,
но у нас знак «минус» да и тройка какая-то
вместо единицы. Поможет следующее
ухищрение, делаем
дробь трехэтажной: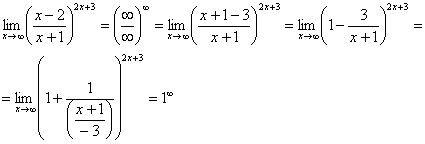
![]() .
Легко
заметить, что в данном примере
.
Легко
заметить, что в данном примере ![]() .
Снова исполняем наш искусственный
прием: возводим основание степени в
.
Снова исполняем наш искусственный
прием: возводим основание степени в ![]() ,
и, чтобы выражение не изменилось –
возводим в обратную дробь
,
и, чтобы выражение не изменилось –
возводим в обратную дробь ![]() :
: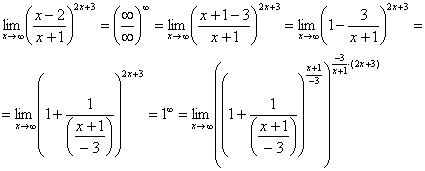
![]() устроено,
с чистой совестью превращаем его в
букву
:
устроено,
с чистой совестью превращаем его в
букву
: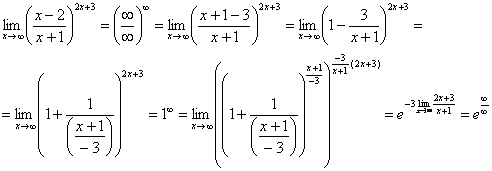
![]() ,
раскрывать такую неопределенность мы
научились на уроке Пределы.
Примеры решений.
Делим числитель и знаменатель на
:
,
раскрывать такую неопределенность мы
научились на уроке Пределы.
Примеры решений.
Делим числитель и знаменатель на
:
![]()
![]()
![]()
![]() .
С помощью знакомого искусственного
приема организуем в показателе степени
конструкцию
.
С помощью знакомого искусственного
приема организуем в показателе степени
конструкцию ![]() :
: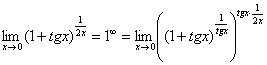
![]() со
спокойной душой превращаем в букву
:
со
спокойной душой превращаем в букву
: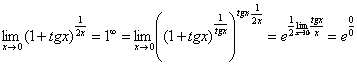
![]() .
Раскладываем тангенс на синус и косинус
(ничего не напоминает?):
.
Раскладываем тангенс на синус и косинус
(ничего не напоминает?):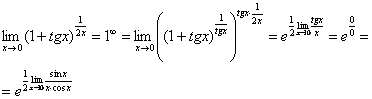

![]() ,
значит в понимании высшей математики
не всё так безнадежно = )
,
значит в понимании высшей математики
не всё так безнадежно = )![]() или
или ![]() ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю. римеры.
римеры.
![]() (см.
рис.).
(см.
рис.).![]() .
.
![]() и
и ![]() .
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдетсяδ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
.
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдетсяδ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.![]() .
.![]() .
.![]() .
Тогда 1/f(x) есть
ограниченная функция. Поэтому дробь
.
Тогда 1/f(x) есть
ограниченная функция. Поэтому дробь ![]() есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.![]() ,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
![]() –
бесконечно малая при x→+∞,
т.е.
–
бесконечно малая при x→+∞,
т.е. ![]() .
.![]() .
.
![]() .
.![]() .
.![]() ,
так как функции
,
так как функции ![]() и
и ![]() -
бесконечно малые при x→+∞,
то
-
бесконечно малые при x→+∞,
то ![]() ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же ![]() является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.![]() .
.![]() .
.![]() .Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
.Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,![]() .
.![]() .
.![]() .
.![]() .
.![]() .
.![]() .
.![]() .
.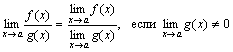 .
.![]() .
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α,
β –
бесконечно малые. Рассмотрим частное
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α,
β –
бесконечно малые. Рассмотрим частное![]() .
.![]() является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
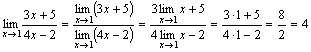 .
.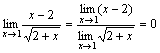 .
.![]() .
При x→1 числитель
дроби стремится к 1, а знаменатель
стремится к 0. Но так как
.
При x→1 числитель
дроби стремится к 1, а знаменатель
стремится к 0. Но так как 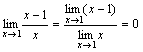 ,
т.е.
,
т.е. ![]() есть
бесконечно малая функция при x→1,
то
есть
бесконечно малая функция при x→1,
то ![]() .
.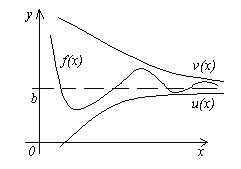 еорема
4. Пусть
даны три функции f(x),
u(x) и v(x),
удовлетворяющие неравенствам u(x)≤f(x)≤
v(x).
Если функции u(x) и v(x) имеют
один и тот же предел при x→a (или x→∞),
то и функция f(x) стремится
к тому же пределу, т.е. если
еорема
4. Пусть
даны три функции f(x),
u(x) и v(x),
удовлетворяющие неравенствам u(x)≤f(x)≤
v(x).
Если функции u(x) и v(x) имеют
один и тот же предел при x→a (или x→∞),
то и функция f(x) стремится
к тому же пределу, т.е. если![]() ,
то
,
то ![]() .
.![]() ,
то имеет место неравенствоb≥c.
,
то имеет место неравенствоb≥c.![]() ,
или
,
или ![]() .
.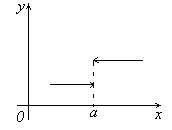 о
сих пор мы рассматривали определение
предела функции, когда x→a произвольным
образом, т.е. предел функции не зависел
от того, как располагалось x по
отношению к a,
слева или справа от a.
Однако, довольно часто можно встретить
функции, которые не имеют предела при
этом условии, но они имеют предел,
если x→a,
оставаясь с одной стороны от а,
слева или справа (см. рис.). Поэтому
вводят понятия односторонних пределов.
о
сих пор мы рассматривали определение
предела функции, когда x→a произвольным
образом, т.е. предел функции не зависел
от того, как располагалось x по
отношению к a,
слева или справа от a.
Однако, довольно часто можно встретить
функции, которые не имеют предела при
этом условии, но они имеют предел,
если x→a,
оставаясь с одной стороны от а,
слева или справа (см. рис.). Поэтому
вводят понятия односторонних пределов.![]() и
называютbпределом
функции f(x) в точке a слева.
и
называютbпределом
функции f(x) в точке a слева.![]() выполняется
неравенство
выполняется
неравенство ![]() .
.![]() и
называют b пределом
функции в точке а справа.
Т.е. число b называется пределом
функции y=f(x) при x→a
справа,
если каково бы ни было положительное
число ε, найдется такое число δ
(большее а),
что для всех
и
называют b пределом
функции в точке а справа.
Т.е. число b называется пределом
функции y=f(x) при x→a
справа,
если каково бы ни было положительное
число ε, найдется такое число δ
(большее а),
что для всех ![]() выполняется
неравенство
.
выполняется
неравенство
.
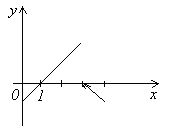 ассмотрим
функцию y=f(x),
определенную на отрезке [0,1] следующим
образом
ассмотрим
функцию y=f(x),
определенную на отрезке [0,1] следующим
образом![]()
![]() ,
а
,
а ![]() .
.
![]() .
.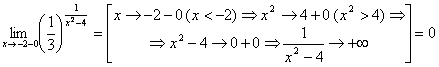 .
.![]()
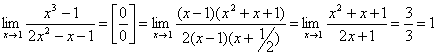 .
.![]() .
.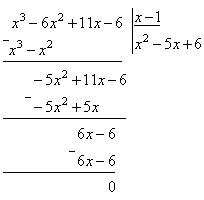

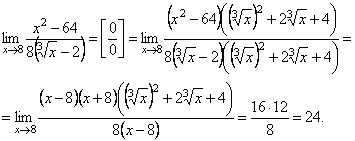
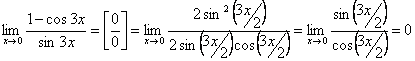 .
.![]() .
.
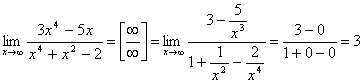 .
.
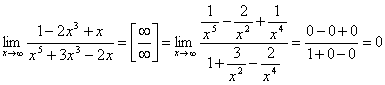 .
.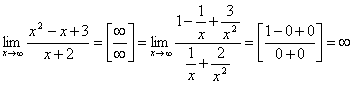 .
.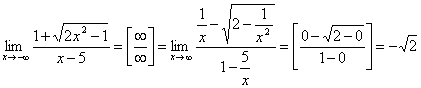 .
.![]() ,если x<0.
,если x<0.![]() .
.

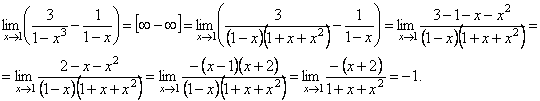
![]() .
.Определение непрерывности функции
![]() определена
на некотором интервале
определена
на некотором интервале ![]() ,
для которого
,
для которого ![]() --
внутренняя точка. Функция
называется непрерывной
в точке
,
если существует предел
при
--
внутренняя точка. Функция
называется непрерывной
в точке
,
если существует предел
при ![]() и
этот предел равен значению
и
этот предел равен значению ![]() ,
то есть
,
то есть![]()
![]() ,
для которого
--
левый конец. Функция
называется непрерывной
справа в точке
,
если существует предел
при
,
для которого
--
левый конец. Функция
называется непрерывной
справа в точке
,
если существует предел
при ![]() и
этот предел равен значению
,
то есть
и
этот предел равен значению
,
то есть![]()
![]() ,
для которого
--
правый конец. Функция
называется непрерывной
слева в точке
,
если существует предел
при
,
для которого
--
правый конец. Функция
называется непрерывной
слева в точке
,
если существует предел
при ![]() и
этот предел равен значению
,
то есть
и
этот предел равен значению
,
то есть![]()
![]() ;
;![]() ;
;![]() .
.
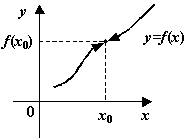
![]() и
и ![]() .
Тогда
.
Тогда ![]() и
и ![]() .
Эти значения совпадают, значит,
функция
.
Эти значения совпадают, значит,
функция ![]() непрерывна
в точке
.
непрерывна
в точке
.![]() --
элементарная функция;
--
точка её области определения
--
элементарная функция;
--
точка её области определения ![]() .
Все элементарные функции непрерывны
во всех внутренних точках своих областей
определения, в том числе и эта. Так что
в этом примере можно было бы заменить
любой
элементарной функцией, а
--
любой внутренней точкой области
.
Все элементарные функции непрерывны
во всех внутренних точках своих областей
определения, в том числе и эта. Так что
в этом примере можно было бы заменить
любой
элементарной функцией, а
--
любой внутренней точкой области ![]() ,
и вывод остался бы тем же.)
,
и вывод остался бы тем же.) 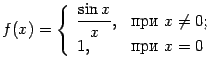 и
точку
.
При
и
точку
.
При ![]() функция
задаётся формулой
функция
задаётся формулой 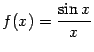 ,
при этом имеем
,
при этом имеем 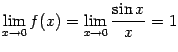 (первый
замечательный предел). Это значение
совпадает с тем, которое задано при
(первый
замечательный предел). Это значение
совпадает с тем, которое задано при ![]() :
: ![]() .
Итак,
.
Итак, ![]() ,
что означает непрервыность функции
при
.
,
что означает непрервыность функции
при
.
![]() --
база непроколотых
окрестностей точки
,
окончаниями которой служат
интервалы
--
база непроколотых
окрестностей точки
,
окончаниями которой служат
интервалы ![]() ,
, ![]() ;
; ![]() --
база непроколотых
левых окрестностей точки
,
окончаниями которой служат
полуинтервалы
--
база непроколотых
левых окрестностей точки
,
окончаниями которой служат
полуинтервалы ![]() ,
;
,
; ![]() --
база непроколотых
правых окрестностей точки
,
окончаниями которой служат
полуинтервалы
--
база непроколотых
правых окрестностей точки
,
окончаниями которой служат
полуинтервалы ![]() ,
.
Тогда непрерывность функции
в
точке
эквивалентна
тому, что существует предел
,
.
Тогда непрерывность функции
в
точке
эквивалентна
тому, что существует предел ![]() ;
непрерывность слева в точке
--
тому, что существует предел
;
непрерывность слева в точке
--
тому, что существует предел ![]() ;
непрерывность справа в точке
--
тому, что существует предел
;
непрерывность справа в точке
--
тому, что существует предел ![]() .
.
![]()
![]() определяемая
равенством
определяемая
равенством ![]()
![]() непрерывна
в точке
непрерывна
в точке ![]() ,
а функция f2 :
Y
,
а функция f2 :
Y![]() Z непрерывна
в точке
Z непрерывна
в точке ![]() ,
то С. ф. f2 о/f1 также
непрерывна в точке х 0 (здесь X,
Y и
Zявляются, напр., топологии, пространствами).
Подобным образом, композиция праз
(непрерывно) дифференцируемых функций
представляет собой также праз (непрерывно)
дифференцируемую функцию, n=1, 2, ...
Композиция возрастающих (убывающих)
функций есть возрастающая (соответственно
убывающая) функция. При композиции
функций иногда меняются количественные
характеристики свойств функций:
композиция функций f1 и f2,
удовлетворяющих условию Гёльдера
нек-рых степеней, есть функция,
удовлетворяющая условию Гёльдера
степени, равной произведению степеней
условий Гёльдера, к-рым удовлетворяют
функции f1 и f2.
Нек-рые характеристики функций не
сохраняются при композиции. Так,
композиция функций, интегрируемых по
Риману или по Лебегу, не является, вообще
говоря, функцией, интегрируемой по
Риману или, соответственно, по Лебегу;
композиция абсолютно непрерывных
функций может оказаться не абсолютно
непрерывной функцией. Вместе с тем,
согласно результатам Н. К. Бари и Д. Е.
Меньшова [1], композиция трех абсолютно
непрерывных на отрезке функций не
приводит к новому классу функций по
сравнению с композицией двух абсолютно
непрерывных функций. Н. К. Бари [2]
доказала, что любая непрерывная на
отрезке функция может быть представлена
в виде суммы трех композиций абсолютно
непрерывных функций, и есть такие
непрерывные функции, к-рые но могут
быть представлены в виде суммы двух
таких композиций. Вместе с тем, всякая
непрерывная на отрезке функция является
суммой двух композиций функций с
ограниченным изменением; однако
n-кратные композиции функций с ограниченным
изменением для каждого п=1,
2, ... приводят
к существенно новым классам функций и
существуют однократные композиции
функций с ограниченным изменением, не
являющиеся непрерывными функциями
[3].
,
то С. ф. f2 о/f1 также
непрерывна в точке х 0 (здесь X,
Y и
Zявляются, напр., топологии, пространствами).
Подобным образом, композиция праз
(непрерывно) дифференцируемых функций
представляет собой также праз (непрерывно)
дифференцируемую функцию, n=1, 2, ...
Композиция возрастающих (убывающих)
функций есть возрастающая (соответственно
убывающая) функция. При композиции
функций иногда меняются количественные
характеристики свойств функций:
композиция функций f1 и f2,
удовлетворяющих условию Гёльдера
нек-рых степеней, есть функция,
удовлетворяющая условию Гёльдера
степени, равной произведению степеней
условий Гёльдера, к-рым удовлетворяют
функции f1 и f2.
Нек-рые характеристики функций не
сохраняются при композиции. Так,
композиция функций, интегрируемых по
Риману или по Лебегу, не является, вообще
говоря, функцией, интегрируемой по
Риману или, соответственно, по Лебегу;
композиция абсолютно непрерывных
функций может оказаться не абсолютно
непрерывной функцией. Вместе с тем,
согласно результатам Н. К. Бари и Д. Е.
Меньшова [1], композиция трех абсолютно
непрерывных на отрезке функций не
приводит к новому классу функций по
сравнению с композицией двух абсолютно
непрерывных функций. Н. К. Бари [2]
доказала, что любая непрерывная на
отрезке функция может быть представлена
в виде суммы трех композиций абсолютно
непрерывных функций, и есть такие
непрерывные функции, к-рые но могут
быть представлены в виде суммы двух
таких композиций. Вместе с тем, всякая
непрерывная на отрезке функция является
суммой двух композиций функций с
ограниченным изменением; однако
n-кратные композиции функций с ограниченным
изменением для каждого п=1,
2, ... приводят
к существенно новым классам функций и
существуют однократные композиции
функций с ограниченным изменением, не
являющиеся непрерывными функциями
[3].![]() может
быть с помощью подстановки (наз.
преобразованием Чирнгаузена) приведено
к виду
может
быть с помощью подстановки (наз.
преобразованием Чирнгаузена) приведено
к виду ![]()
![]() представляет
собой функцию п-4
параметров. Задача состоит в выяснении:
можно ли эти функции представить в виде
композиции алгебраич. функций меньшего
числа неременных. Одна из 23 проблем Д.
Гильберта (D. Hilbert), поставленных им на
Международном конгрессе математиков
в Париже в 1900, относилась к этой задаче.
Именно, 13-я проблема состояла в следующем
(см. [4]): представляется ли корень f
уравнения
представляет
собой функцию п-4
параметров. Задача состоит в выяснении:
можно ли эти функции представить в виде
композиции алгебраич. функций меньшего
числа неременных. Одна из 23 проблем Д.
Гильберта (D. Hilbert), поставленных им на
Международном конгрессе математиков
в Париже в 1900, относилась к этой задаче.
Именно, 13-я проблема состояла в следующем
(см. [4]): представляется ли корень f
уравнения ![]() (*)
(*)![]() ,
то можно указать праз дифференцируемую
функцию тпеременных, непредставимую
в виде композиции n1 раз
дифференцируемых функций от m1 переменных.
В частности, при всяком пможно указать
функцию ппеременных наперед заданной
гладкости, непредставимую композицией
функций меньшего числа переменных той
же гладкости. В этом смысле среди гладких
функций любого числа переменных
существуют функции, существенно
зависящие от всех своих аргументов.
,
то можно указать праз дифференцируемую
функцию тпеременных, непредставимую
в виде композиции n1 раз
дифференцируемых функций от m1 переменных.
В частности, при всяком пможно указать
функцию ппеременных наперед заданной
гладкости, непредставимую композицией
функций меньшего числа переменных той
же гладкости. В этом смысле среди гладких
функций любого числа переменных
существуют функции, существенно
зависящие от всех своих аргументов.![]() )
кубе непрерывная
функция является
композицией непрерывных функций трех
переменных. Затем В. И. Арнольд
уменьшил число переменных
с трех до двух. Именно, он доказал [12],
что любую непрерывную на кубе функцию
трех переменных можно представить в
виде композиции непрерывных функций
двух переменных (и даже, более точно, в
виде суммы 9 функций, каждая из к-рых
является однократной композицией
непрерывных функций двух переменных).
Тем самым было показано, что каждая
непрерывная на n-мерном (
)
кубе непрерывная
функция является
композицией непрерывных функций трех
переменных. Затем В. И. Арнольд
уменьшил число переменных
с трех до двух. Именно, он доказал [12],
что любую непрерывную на кубе функцию
трех переменных можно представить в
виде композиции непрерывных функций
двух переменных (и даже, более точно, в
виде суммы 9 функций, каждая из к-рых
является однократной композицией
непрерывных функций двух переменных).
Тем самым было показано, что каждая
непрерывная на n-мерном (![]() )
кубе функция представит в виде композиции
непрерывных функций двух переменных.
Это явилось последним словом по
опровержению гипотезы Гильберта о
невозможности представления корней
уравнения (*) в виде композиций непрерывных
функций двух неременных. Работы А. Н.
Колмогорова и В. И. Арнольда дали, в
частности, положительный ответ на
вопрос о представимости корней алгебраич.
уравнений любой степени в виде композиции
непрерывных функций не более чем двух
переменных. Для композиций аналитич.
и алгебраич. функций аналогичный вопрос
не решен. До сих пор (1983) неизвестно,
являются ли корни уравнения (*) композицией
аналитич. ций или нет.
)
кубе функция представит в виде композиции
непрерывных функций двух переменных.
Это явилось последним словом по
опровержению гипотезы Гильберта о
невозможности представления корней
уравнения (*) в виде композиций непрерывных
функций двух неременных. Работы А. Н.
Колмогорова и В. И. Арнольда дали, в
частности, положительный ответ на
вопрос о представимости корней алгебраич.
уравнений любой степени в виде композиции
непрерывных функций не более чем двух
переменных. Для композиций аналитич.
и алгебраич. функций аналогичный вопрос
не решен. До сих пор (1983) неизвестно,
являются ли корни уравнения (*) композицией
аналитич. ций или нет.![]() ,
,![]()
![]() выполняется
условие -
выполняется
условие - ![]() .
.![]() ,
ограничена в некоторой ее окрестности,
а если разбивать отрезок
на
бесконечное количество отрезков,
которые “стягиваются” к точке
,
то образуется некоторая окрестность
точки
.
,
ограничена в некоторой ее окрестности,
а если разбивать отрезок
на
бесконечное количество отрезков,
которые “стягиваются” к точке
,
то образуется некоторая окрестность
точки
.![]() и
и ![]() ,
что
,
что ![]() ,
причем
,
причем ![]() .
.![]() ).
).![]() непрерывна
в точке
непрерывна
в точке ![]() ,
то существует некоторая окрестность
точки
,
в которой функция сохраняет знак.
,
то существует некоторая окрестность
точки
,
в которой функция сохраняет знак.![]() .
.![]() ,
то
,
то ![]() .
.![]() существует
существует ![]() такое,
что для любых точек
такое,
что для любых точек ![]() и
и ![]() таких,
что
таких,
что ![]() верно
неравенство
верно
неравенство ![]() .
.![]() ,
не зависящее от
,
не зависящее от ![]() ,
а при “обычной” непрерывности
зависит
от
,
а при “обычной” непрерывности
зависит
от ![]() и
.
и
.![]() тоже
однозначна, монотонна и непрерывна.
тоже
однозначна, монотонна и непрерывна.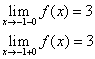
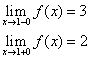 в
точке
в
точке ![]() функция
непрерывна в точке
функция
непрерывна в точке
![]()
§ 3.7. Равномерная непрерывность функции
![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() (или
интервале, полуинтервале). Тогда для
каждой точки
(или
интервале, полуинтервале). Тогда для
каждой точки ![]() этого
отрезка (интервала, полуинтервала) по
заданному
этого
отрезка (интервала, полуинтервала) по
заданному ![]() найдется
найдется ![]() такое,
что
такое,
что![]() ,
,![]() .
.![]() при
постоянном
при
постоянном ![]() число
число ![]() ,
вообще говоря, изменяется – оно зависит
не только от
,
но и от
.
Как видно из рис. 29, число
,
пригодное на участке с пологим графиком,
может оказаться слишком большим для
участка с круто поднимающимся графиком.
,
вообще говоря, изменяется – оно зависит
не только от
,
но и от
.
Как видно из рис. 29, число
,
пригодное на участке с пологим графиком,
может оказаться слишком большим для
участка с круто поднимающимся графиком.
![]() ,
принадлежащих тому множеству, где
задана функция.
,
принадлежащих тому множеству, где
задана функция.![]() ,
называется равномерно непрерывной на
этом множестве, если для всякого
найдется
,
зависящее только от
,
называется равномерно непрерывной на
этом множестве, если для всякого
найдется
,
зависящее только от ![]() ,
такое, что
,
такое, что![]()
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ![]() .
.![]()
![]() .
Обратное, вообще говоря, неверно.
.
Обратное, вообще говоря, неверно.![]() определена
и непрерывна на отрезке
,
то она равномерно непрерывна на нем.
определена
и непрерывна на отрезке
,
то она равномерно непрерывна на нем.![]() ,
что для любого
найдется
пара точек
,
что для любого
найдется
пара точек ![]() ,
удовлетворяющих неравенству
,
для которых
,
удовлетворяющих неравенству
,
для которых![]() .
.![]() .
Для каждого
.
Для каждого ![]() найдутся
точки
найдутся
точки ![]() такие,
что
такие,
что![]() ,
но
,
но ![]() .
(1)
.
(1)![]() принадлежат
к
,
то эта последовательность ограничена
и из нее по теореме Больцано-Вейерштрасса
можно выделить подпоследовательность
принадлежат
к
,
то эта последовательность ограничена
и из нее по теореме Больцано-Вейерштрасса
можно выделить подпоследовательность ![]() ,
сходящуюся к некоторой точке
,
сходящуюся к некоторой точке ![]() .
Так как
.
Так как ![]() ,
, ![]() ,
то подпоследовательность
,
то подпоследовательность ![]() тоже
сходится к точке
.
По условию функция
непрерывна
на
тоже
сходится к точке
.
По условию функция
непрерывна
на ![]() и,
следовательно, непрерывна в точке
.
Конечно, если
и,
следовательно, непрерывна в точке
.
Конечно, если ![]() или
или ![]() ,
то надо считать, что
непрерывна
в
справа
или соответственно слева. Поэтому
,
то надо считать, что
непрерывна
в
справа
или соответственно слева. Поэтому![]() .
.![]() ,
(2)
,
(2)![]() .
.![]() (см.
§ 3.3,
пример 8). Теорема доказана.
(см.
§ 3.3,
пример 8). Теорема доказана.![]()
![]() ,
поэтому на основании теоремы 1 она
равномерно непрерывна на этом отрезке.
,
поэтому на основании теоремы 1 она
равномерно непрерывна на этом отрезке.![]() эта
функция хотя и непрерывна, но не является
равномерно непрерывной. Это показывает,
что требование в теореме 1, чтобы
непрерывная функция была задана на
отрезке, а не на интервале, существенно.
эта
функция хотя и непрерывна, но не является
равномерно непрерывной. Это показывает,
что требование в теореме 1, чтобы
непрерывная функция была задана на
отрезке, а не на интервале, существенно.![]() ,
очевидно, принадлежат полуинтервалу
,
и для них
,
очевидно, принадлежат полуинтервалу
,
и для них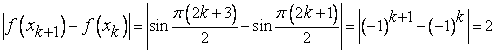 .
.![]() ,
то при любом
найдется
такое
,
то при любом
найдется
такое ![]() ,
что
,
что![]() ,
,![]() .
.![]() ,
доопределив ее в точке
,
доопределив ее в точке ![]() так,
чтобы она стала непрерывной на
,
потому что тогда, согласно теореме 1,
она была бы равномерно непрерывной
на
,
а следовательно, и на
,
чего быть не может.
так,
чтобы она стала непрерывной на
,
потому что тогда, согласно теореме 1,
она была бы равномерно непрерывной
на
,
а следовательно, и на
,
чего быть не может.![]() ,
то функция называется непрерывной
справа.
,
то функция называется непрерывной
справа.

х0
Если
односторонний предел (см. выше) ![]() ,
то функция называется непрерывной
слева.
,
то функция называется непрерывной
слева.
|
|
|
|
х0
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
![]()
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
![]()
не является непрерывной в любой точке х0.
Пример. Функция f(x)
= ![]() имеет
в точке х0 =
0 точку разрыва 2 – го рода, т.к.
имеет
в точке х0 =
0 точку разрыва 2 – го рода, т.к.
![]() .
.
![]()
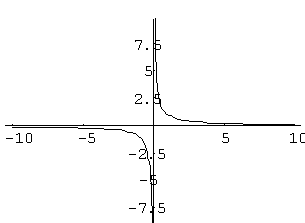
Пример. f(x)
= ![]()
Функция
не определена в точке х = 0, но имеет в
ней конечный предел ![]() ,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
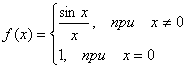
График этой функции:
Пример. f(x)
= ![]() =
=![]()
 y
y
1
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.