Достаточные условия экстремума

Пусть функция   u = f(x₁, x₂,  … , x_n)  имеет непрерывные частные производные до 2–го порядка включительно в некоторой окрестности ее стационарной точки  M₀(x₁⁰, x₂⁰,  … , x_n⁰) .

Пусть   M(x₁⁰ + dx₁, x₂⁰ + dx₂,  … , x_n⁰ + dx_n) — некоторая точка из этой окрестности. Тогда

Δu = f(x10 + dx1,x20 + dx2, … ,xn0 + dxn) − f(x10,x20, … ,xn0)

— приращение функции, которое она получает при смещении из точки M₀ в точку M .

По формуле Тейлора имеем

Δz = dz(M0) +  1 2!   d2z(M0) + o(ρ2)

где ρ — расстояние между точками M₀ и M .

Так как M₀ — стационарная точка функции u = f(x₁, … ,x_n) , то dz(M₀) = 0 .

Допустим, что d²z(M₀) ≠ 0 для всех точек M из некоторой окрестности O_δ(M₀), достаточно малой, чтобы в ней выполнялось неравенство |d²z(M₀)| > |o(ρ²)| . Тогда знаки Δz иd²z(M₀) одинаковы .

Если d²z(M₀)>0 для всех точек M из окрестности O_δ(M₀) то и Δz > 0. В этом случае функция u = f(x₁, … ,  x_n) имеет минимум в точке M₀ .

Если d²z(M₀)<0 для всех точек M из окрестности O_δ(M₀), то и Δz < 0. В этом случае функция u = f(x₁, … ,x_n) имеет максимум в точке M₀ .

Таким образом, достаточным условием экстремума функции нескольких переменных в ее стационарной точке является знакоопределенность (положительная или отрицательная определенность) дифференциала 2–го порядка в этой точке.

Достаточные условия экстремума функции 2–х переменных

Теорема. Пусть функция z = f(x, y) определена и имеет непрерывные частные производные второго порядка в стационарной точке   M(x₀, y₀) (т.е.   z'_x (x₀, y₀) = z'_y(x₀, y₀) = 0 ):

A = z''xx(x0, y0),  B = z''xy(x0, y0),  C = z''yy(x0, y0).

Тогда:

• если AC − B²0 , то M — точка экстремума, причем при A0 — точка минимума, при A<0 — точка максимума;

• если AC − B²<0 ,  то M не является точкой экстремума;

• если AC − B² = 0 , то требуется дополнительное исследование.

Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М.: Изд–во МЭИ, 2002 (стр. 163).



Выпуклость, вогнутость функции, точка перегиба.

Определение.

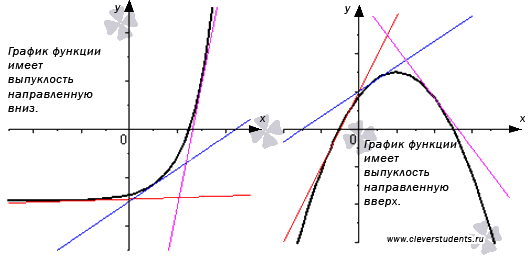
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Определение.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

Определение.

Точка   называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.

Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.

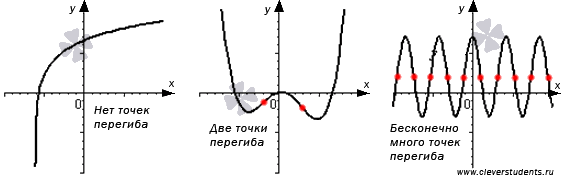
На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

К началу страницы