Понятие последовательности
Если функция определена на множестве натуральных чисел N, то такая функция называется бесконечной числовой последовательностью. Обычно числовые последовательность обозначают как(Xn), где n принадлежит множеству натуральных чисел N.
Числовая последовательность может быть задана формулой. Например, Xn=1/(2*n). Таким образом мы ставим в соответствие каждому натуральному числу n некоторый определенный элемент последовательности (Xn).
Если теперь последовательно брать n равными 1,2,3, …., мы получим последовательность (Xn): ½, ¼, 1/6, …, 1/(2*n), …
Виды последовательности
Последовательность может быть ограниченной или неограниченной, возрастающей или убывающей.
Последовательность (Xn) называет ограниченной, если существуют два числа m и M такие, что для любого n принадлежащего множеству натуральных чисел, будет выполняться равенство m<=Xn
Последовательность (Xn), не являющаяся ограниченной, называется неограниченной последовательностью.
Последовательность (Xn) называется возрастающей, если для всех натуральных n выполняется следующее равенство X(n+1) > Xn. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена.
Последовательность (Xn) называется убывающей, если для всех натуральных n выполняется следующее равенство X(n+1) < Xn. Иначе говоря, каждый член последовательности, начиная со второго, должен быть меньше предыдущего члена.
Пример последовательности
Проверим, являются ли последовательности 1/n и (n-1)/n убывающими.
Если последовательность убывающая, то X(n+1) < Xn. Следовательно X(n+1) – Xn < 0.
1/n:
X(n+1) – Xn = 1/(n+1) – 1/n = -1/(n*(n+1)) < 0. Значит последовательность 1/n убывающая.
(n-1)/n:
X(n+1) – Xn =n/(n+1) - (n-1)/n = 1/(n*(n+1)) > 0. Значит последовательность (n-1)/n возрастающая.
Свойства пределов, связанные с арифметическими операциями над последовательностями
Править 
Обсуждение0
1831СТАТЬЯ НА ЭТОЙ ВИКИ
1. Сумма сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме пределов исходных последовательностей.
Доказательство .
Пусть 
, 
, 
,
-
бесконечно малая последовательность, 
, 
-
бесконечно малая последовательность.
2. Если
,
,
то 
3. Если
,
,
то 
Доказательство .
, - бесконечно малая последовательность, , - бесконечно малая последовательность.
,
где
Лемма .
Если
≠ 
,
то начиная с некоторого номера определена
последовательность 
которая
является ограниченной.
Доказательство .
Положим 
При 
при
при
4. Если
,
≠
0, то 
= 
Доказательство .
В
силу леммы начиная с некоторого номера
N элементы последовательности 
ограничена.
Сэтого номера будем рассматривать
последовательность 
,
-
бесконечно малая последовательность.
,
-
бесконечно малая последовательность.
-
бесконечно малая последовательность.
Сходящиеся последовательности и их свойства. Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число а, что последовательность {xn−a} является бесконечно малой. Если последовательность {xn→a } является сходящейся и имеет своим пределом число a, то символически это записывают так:limn→∞xn=a или xn→a при n→∞ Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число a, что для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всехn>Nэлементы xn этой последовательности удовлетворяют неравенству ∣xn−a∣<ε При этом число a называется пределом последовательности. Неравенство (5) можно записать в эквивалентной форме −ε<xn−a<+ε или, a−ε<xn<a+ε . (5') Определение. Последовательность {xn} называется сходящейся, если существует такое число a, что в любой ε-окрестности точки aнаходятся все элементы последовательности {xn} начиная с некоторого номера (зависящего от ε). Теорема 1. Сходящаяся последовательность имеет только один предел. Доказательство. Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a . Последовательность {an−bn} является бесконечно малой, а в силу равенства an−bn=b−a все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числуb−a . Число b−a равно нулю, т. е. b=a. Теорема доказана.
Теорема 2. Всякая сходящаяся последовательность является ограниченной.
Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε при n≥N или, a−ε<xn<a+ε при n≥N . Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣ ∣ x1∣ ∣ ,∣ ∣ x2∣ ∣ ,...,∣ ∣ хN−1∣ ∣ . Тогда, очевидно, ∣xn∣≤A для всех номеров n, а это и доказывает ограниченность последовательности{xn}. Теорема доказана.
Следствие 1. Не всякая ограниченная последовательность является сходящейся. Так, например, посл. 0,1,0,1,...,0,1, ... является ограниченной, но не является сходящейся. В самом деле, обозначим n-й член этой последовательности символом xn и предположим, что эта последовательность сходится к некоторому пределу a. Но тогда каждая из последовательностей {xn+1−a} и {xn−a} являлась бы бесконечно малой. Стало быть, являлась бы бесконечно малой и разность этих последовательностей {xn+1−xn} а этого быть не может в силу того, что ∣ ∣ xn+1−xn∣ ∣ =1 для всех номеров n. Последовательность {an} называется бесконечно малой, если для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>Nэлемент an последовательности удовлетворяет неравенству ∣an∣<ε .
Теорема 3. Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам а и b соответственно. Тогда в силу того что xn=a+an будут справедливы соотношения xn=a+an,yn=b+bn, (6), в которых anи bn представляют собой элементы некоторых бесконечно малых последовательностей {an}и {bn}. Из (6) вытекает, что(xn+yn)−(a−b)=an+bn . (7) Т.к. сумма {an+bn} двух бесконечно малых последовательностей {an} и {bn} представляет собой бесконечно малую последовательность, то из соотношения (7) вытекает в силу определения, что последовательность {xn+yn} сходится и вещественное число a+b является ее пределом. Теорема доказана.
Теорема 4. Разность сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {xn} и {yn} Доказательство этой теоремы аналогично доказательству Теоремы 3, только вместо соотношения (7) мы получим соотношение (xn−yn)−(a−b)=an−bn .
Теорема 5. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn}сходятся к пределам a и bсоответственно. Тогда для элементов этих последовательностей справедливы (6), перемножая которые, мы получим xn·yn=a·b+abn+ban+an·bn или, xnyn−a·b=abn+ban+an·bn (8) Лемма 1. Если последовательность {yn} сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное {1yn} последовательностей {\{}1{\}} и {yn}, которое представляет собой ограниченную последовательность.
Теорема 6. Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам a и bсоответственно. В силу леммы 1 найдется номер N такой, что при n>N элементы yn нe обращаются в нуль, определена последовательность {1yn} и эта последовательность является ограниченной. Начиная с номера N, мы и будем рассматривать частное {ynxn} . В силу определения достаточно доказать, что последовательность {ynxn−ba} является бесконечно малой. Будем исходить из тождества ynxn−ba=yn·bxn·b−yn·a (9) Т.к. для элементов xn и yn справедливы (6), то
n·b−yn·a=(a+an)·bn−(b+bn)·an=anb−bna
Подставляя (10) в (9), получим ynxn−ba=1yn(an−babn) (11) Остается доказать, что в правой части (11) стоит элемент бесконечно малой последовательности, но это сразу вытекает из того, что последовательность {1yn} (в силу леммы 1) является ограниченной, а последовательность {an−babn} (как разность двух бесконечно малых) является бесконечно малой последовательностью. Теорема доказана.
Определение предела по Коши и по Гейне, их эквивалентность
1 комментарий
1. Определение предела по Коши и по Гейне
Определение
1.1. (определение по Коши или на языке 
):
—
предел
функции 
в
точке 
(и
пишут 
),
если: 
В
определении допускается, что 
,
то есть
может
не принадлежать области
определения функции.
Определение 1.2. (определение по Гейне):
называется
пределом функции
в
точке
,
если 
,
то есть 
,
соответствующая последовательность
значений 
, то
есть 
.
Замечание 1.1.
Из определения предела функции по Гейне следует, что функция не может иметь в точке два разные предела.
Замечание 1.2.
Понятие предела функции в точке есть локальное понятие: существование и значение предела полностью определяется значениями функции в как угодно малой окрестности этой точки.
Замечание 1.3.
Данную
запись в определении можно сформулировать
иначе: точка 
принадлежит
проколотой 
-окрестности
точки
(
)
2. Эквивалентность определений
Пусть
число
является
пределом функции
в
точке
по
Коши. Выберем произвольную
подходящую последовательность 
, 
,
то есть такую, для которой
.
Покажем, что
является
пределом по Гейне.
Зададим
произвольное 
и
укажем для него такое 
,
что для всех
из
условия 
следует
неравенство 
.
В силу того, что
,
для
найдётся
такой номер 
,
что 
будет
выполняться неравенство 
,
то есть
.
Докажем
теперь обратное утверждение: предположим,
что
по
Гейне, и покажем, что число
является
пределом функции
в
точке
по
Коши. Предположим, что это неверно, то
есть: .
В качестве
рассмотрим 
,
а соответствующие значения 
будем
обозначать
.
Тогда при любом
выполняются
условия 
и 
.
Отсюда следует, чтопоследовательность 
является
подходящей, но число
не
является пределом функции
в
точке
.
Получили противоречие.
3. Примеры
Пример 3.1.
а) 
,
например 
б) 
Пример 3.2.
Доказать,
что 
не
имеет предела в точке 0.
Вывод: последовательность по Гейне не имеет предела.
Бесконечно большая последовательность[править]
Определение. Последовательность 
называется бесконечно
большой, если для любого положительного
числа A можно
указать номер N такой,
что при 
все
элементы 
этой
последовательности удовлетворяют
неравенству 
.
Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, ... 1, n, ... не является бесконечно большой, так как при A > 1 неравенство не выполняется для с нечетными номерами.
Бесконечно малая последовательность[править]
Определение. Последовательность
называется бесконечные
малой, если для любого положительного
числа ε можно
указать номер N такой,
что при
все
элементы
этой
последовательности удовлетворяют
неравенству 
.
Любая бесконечно малая последовательность является ограниченной [1].
Свойства бесконечно малых последовательностей |
|
|
|
Свойство
1. Произведение бесконечно малой
последовательности
для всех n > N, что доказывает утверждение. Следствие. Умножиение бесконечно малой последовательности на любое число дает бесконечно малую последовательность.
Свойство
2. Сумма любого конечного числа
бесконечно малых величин есть величина
бесконечно малая.
Доказательство.
Рассмотрим сначала сумму двух бесконечно
малых величин
Аналогично,
Обозначим
символом N наибольший из
номеров
и
выражающее справедливость доказываемого утверждения. Переходя к случаю суммы произвольного конечного числа бесконечно малых величин, заметим, что любая пара бесконечно малых в этой сумме может быть представлена одной бесконечно малой. Затем каждая пара полученных бесконечно малых может быть заменена одной бесконечно малой и так далее, что в конечном итоге позволит свести рассматриваемую сумму к единственной бесконечно малой. |
|
и ограниченной последовательности
есть бесконечно малая последовательность
.
Доказательство.
Ограниченность последовательности
означает, что 
для всех 
,
где B – некоторое положительное
число. Выберем сколь угодно малое
число ε > 0. Согласно определению
бесконечно малой последовательности
существует такой номер N, начиная
с которого величины 
становятся меньше любого положительного
числа и, в частности, 
.
Тогда
и 
.
Пусть
ε – произвольное положительное
число. Тогда существуют номер 
,
начиная с которого бесконечно малые
величины
становятся меньше числа 
:
.
Тогда для всех номеров n > N
выполняется неравенство
§ 128. Монотонные последовательности
Если каждый член последовательности, начиная со второго, больше предыдущего, то последовательность называется монотонно возрастающей.
Другими словами, числовая последовательность a1, a2, a3, ... называется монотонно возрастающей, если для любого п
an+1 > an
Если при любом n an+1 > an , то последовательность {an} называется монотонно неубывающей. Например, последовательность 1, 1, 2, 2, 3 , 3,... не является монотонно возрастающей, но является монотонно неубывающей.
Примером монотонно возрастающей числовой последовательности является натуральный ряд чисел 1, 2, 3, 4 ... . Другим примером монотонно возрастающей числовой последовательности может служить последовательность
p4, p8, p16, p32, ...
периметров правильных 4-, 8-, 16-угольников и т. д., в п и с а н н ы х в одну и ту же окружность. Действительно, пусть АВ — сторона квадрата, вписанного в окружность О (рис. 199).
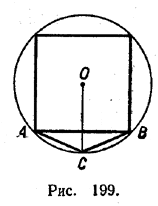
Опустим на АВ перпендикуляр из центра окружности О и продолжим его до пересечения с окружностью в точке С. АС и ВС будут, очевидно, сторонами правильного восьмиугольника. В треугольнике ABC
АС + ВС > АВ.
Поскольку p4 = 4 АВ, p8 = 4 (АС+ВС), то p8 > p4 . Аналогично показывается, чтоp16 > p8 , p32 > p16 и т. д.
Если каждый член числовой последовательности, начиная со второго, меньше предыдущего, то последовлтельность называется монотонно убывающей.
Другими словами, числовая последовательность a1, a2, a3, ... называется монотонно убывающей, если для любого п
an+1 < an
Если при любом п an+1 < an , то последовательность {an} называется монотонно невозрастающей. Например, последовательность 1, 1, 1/2, 1/2, 1/3, 1/3 , , не является монотонно убывающей, но является монотонно невозрастающей.
Примером монотонно убывающей числовой последовательности может служить последовательность
1, 1/2, 1/3, 1/4, ...., 1/n , ... .
Другим примером монотонно убывающей последовательности является последовательность
Р4 , Р8 , Р16 , Р32 ,...
периметров правильных 4-, 8-, 16-угольников и т. д., описанных около одной и той же окружности. Доказательство этого факта мы предлагаем учащимся провести самостоятельно.
Монотонно возрастающие и монотонно убывающие последовательности иногда называются просто монотонными последовательностями.
Не следует думать, что всякая числовая последовательность является монотонной. Так, например, последовательность
—1; 1; —1; 1; ...
с общим членом an = (—1)n не принадлежит ни к монотонно возрастающим, ни к монотонно убывающим последовательностям. То же самое можнэ сказать и о последовательности
1, —1/2, 1/3, —1/4, 1/5 , ....
с
общим членом 
.
Подобные последовательности
получили
название колеблющихся последовательностей.
Упражнения
935. Какие из данных последовательностей являются возрастающими, какие убывающими и какие колеблющимися:
а) 1, 3, 5,...., 2п — 1, ... ;
б) 1, 1/2, 1/3, ...., 1/n , ... ;
в) sin 1, sin 2, sin3..... sin n, ... ;
г) tg π/3, tg π/6, tg π/9 , ....., tg π/3n , ...
д) 1, 4, 9, .... , n2 ...;
е) 1; — 0,1; 0,01; — 0,001; ... ; (— 0,1) n — 1;
936.
Доказать, что последовательность
с общим членом 
является
возрастающей.
937.
Доказать, что последовательность с
общим членом 
является
убывающей.
938.
Какому условию должны удовлетворять
положительные числа а, b, с и d,
чтобы последовательность с общим
членом 
была
монотонно возрастающей?
939.
Доказать, что последовательность
с общим членом 
,
где а — некоторое
положительное число,
отличное от 1, является монотонно
возрастающей.
ОТВЕТЫ
