Относительные показатели вариации.

Используются при сравнении колеблемости признака в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической.

Эти показатели вычисляются как отношение абсолютных показателей вариации к средней арифметической или медиане:

• коэффициент осцилляции:

• относительное линейное отклонение (линейный коэффициент вариации):

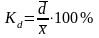
• коэффициент вариации:

Самый используемый показатель – коэффициент вариации:

• для сравнения оценки вариации;

• для характеристики однородности совокупности.

Совокупность однородна, если .

Виды дисперсий.

Если статистическая совокупность разбита на группы по какому либо признаку, то для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, может использоваться разложение общей дисперсии на составляющие: на межгрупповую и внутригрупповую дисперсию.

Общая дисперсия - дисперсия признака по всей изучаемой совокупности – характеризует вариацию признака как результат влияния всех факторов.

Вариацию, обусловленную влиянием фактора, положенного в основу группировки характеризует межгрупповая дисперсия 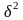, которая является мерой колеблемости частных средних по группам вокруг общей средней :

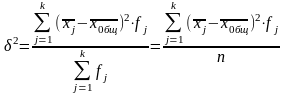
k – число групп;

f_j – число единиц в j-й группе;

- среднее в j-й группе;

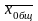- общая средняя.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия (частная групповая дисперсия) - .

По всей совокупности вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий:

.

Связь между (немец Лексис) – правило сложения дисперсий:

.

Оценка вариации качественных признаков.

При оценке вариации качественных признаков оценивается наличие или отсутствие какого-либо признака. Для обозначения наличия признака вводится эквивалент – 1 , для обозначения отсутствия признака у единицы совокупности – эквивалент – 0. Пусть f единиц совокупности обладают некоторым признаком, тогда n-f единиц совокупности на обладают признаком. Ряд распределения в этом случае имеет вид:

Переменная (x)	частота	частость
1	f	p
0	n-f	q
итого	n	1

Где p= , , p+q=1.

Определим значение средней арифметической для качественного признака:

Следовательно, доля единиц совокупности, обладающих признаком равна p, а доля единиц совокупности, не обладающих признаком равна q.

Определим значение дисперсии для качественного признака:

Если значения p и q встречаются одинаково часто, т.е. p=q, то дисперсия достигает своего максимума, pq=0.25.

Среднее квадратическое отклонение: .

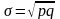Правило сложения дисперсий для доли признака (для качественных признаков): общая дисперсия:

внутригрупповая дисперсия:

Средняя из групповых:

Межгрупповая: , где

Правило сложения дисперсий:

9