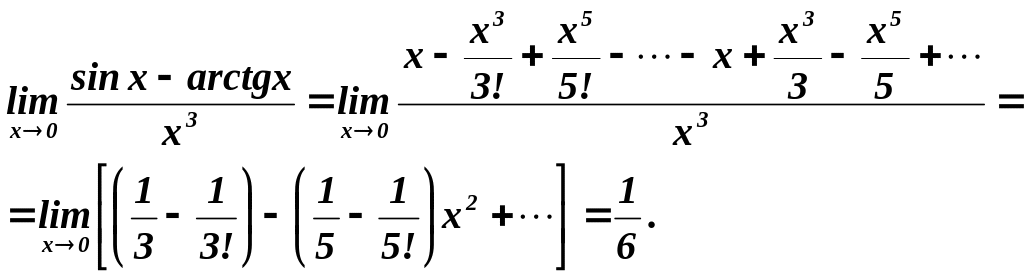7 . Розклад функції в ряд Тейлора і Маклорена.
Для прикладних задач дуже важливо вміти розкласти задану функцію в степеневий ряд, тобто функції надати вигляд суми степеневого ряду. Це дозволяє досить просто обчислювати її значення.
а) Ряд Тейлора.
Припустимо,
що функція
нескінчене число раз диференційована
в околі деякої точки
і її можна представити у вигляді суми
степеневого ряду
(4)
де
невизначені поки що коефіцієнти.
Покажемо,
як можна знайти ці коефіцієнти, знаючи
значення функції
і її похідних в точці
Покладемо
в рівності (1)
Будемо мати
Продиференціюємо степеневий ряд
і
знову покладемо
Тоді
Аналогічно
знаходимо
і
тобто
Після n-кратного диференціювання одержимо
тобто
Підставивши
знайдені коефіцієнти
в (4) отримаємо ряд Тейлора функції
:
(5)
Приклад
1.
Розкласти многочлен
за зростаючими степенями
.
Розв’язання.
Продиференціювавши функцію
одержимо
...
Підставивши
одержимо
Ряд
Тейлора для функції
,
згідно (2), матиме вигляд
б)Ряд Маклорена.
Для
нескінченно диференційованої функції
,
яка допускає розклад за зростаючими
степенями
,
ряд Маклорена має вигляд (частковий
випадок ряду Тейлора при
(6)
Приклад
2.
Розкласти в ряд Маклорена функцію
Розв’язування.
Маємо
,
Поклавши
,
одержимо
Підставивши ці значення в ряд Маклорена (6), одержимо
.
Застосувавши ознаку Даламбера до ряду, складеного з абсолютних величин, маємо
Отже
степеневий ряд для функції
збіжний для будь-якого
Аналогічно отримуємо розклад інших елементарних функцій в ряд Маклорена :
,
-
біноміальний
ряд збігається для
8.Інтегрування і диференціювання степеневих рядів.
Приведемо дві важливі теореми без доведення.
.
Теорема 1. Степеневий ряд (7)
і
отриманий із нього почленним
диференціюванням ряд
(8)
має
один і той же інтервал збіжності
Сума
ряду (8) дорівнює похідній
суми
ряду (7) при всіх значеннях
,
для яких
Теорема
2.
Степеневийй ряд
(9)
і ряд
(10)
одержаний
із ряду (9) почленним інтегруванням,
мають одинаковий інтервал збіжності..
Сума ряду (10) рівна
де
сума ряду (9).
Приклад
3.
Розкласти в степеневий ряд функцію
.
Розв’язування.
Представимо функцію
у виді ряду нескінченно спадної
геометричної прогресії. Тоді
при
Проінтегрувавши почленно, одержимо:
,
Але
тоді
(для
Аналогічно отримуємо розклади інших елементарних функцій в степеневий ряд :
(для
(для
).
9.Застосування степеневих рядів для наближених обчислень.
Одержані в попередніх підрозділах розклади деяких функцій в степеневі ряди дають можливість наближено обчислювати значення функції, визначені та невизначені інтеграли, границі функцій і т.д.
Приклад
1. Обчислити
,
обмежившись двома членами розкладу.
Розв’язування.
Використаємо формулу розкладу в ряд
cos
x
за
зростаючими степенями
.
Переведемо 50
у радіанну міру:
Тоді
Приклад
2.
Обчислити
Роз’язування.
Замінюючи в рівності
на
одержимо:
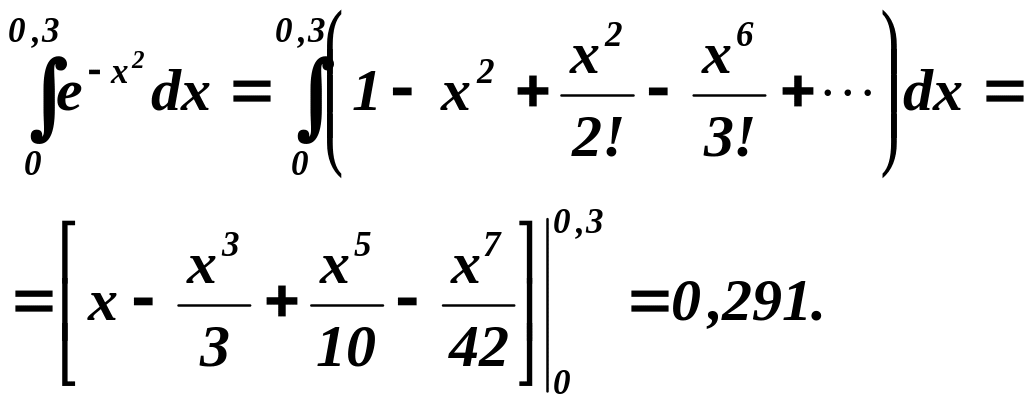
Приклад
3.
Знайти
.
Розв’язування. Оскільки
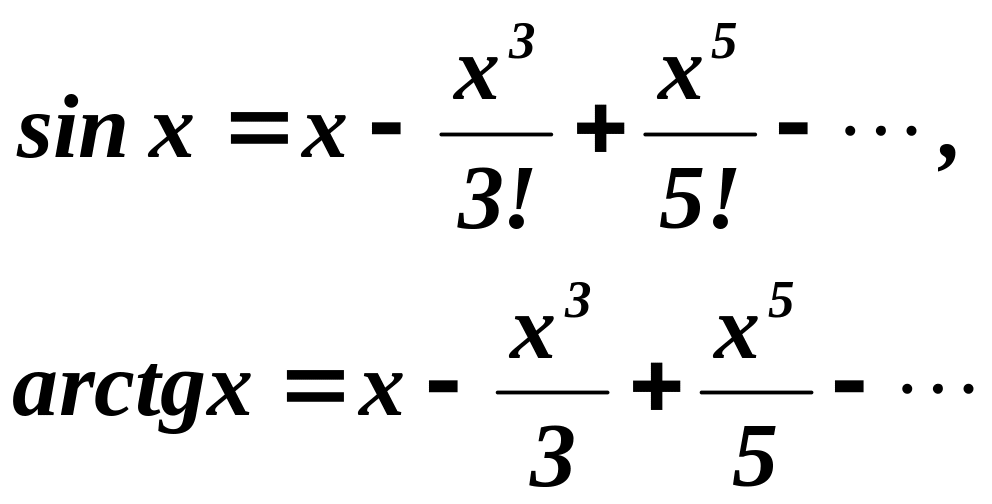
то
