
- •§10. Числові та степеневі ряди
- •Числовий ряд та його збіжність.
- •3.Достатні ознаки збіжності знакопостійних рядів:
- •4.Знакозмінні ряди. Ознака Лейбніца збіжності знакопереміжного ряду.
- •5. Абсолютна та умовна збіжність ряду.
- •6.Степеневий ряд та його збіжність. Область збіжності степеневого ряду.
- •7 . Розклад функції в ряд Тейлора і Маклорена.
- •8.Інтегрування і диференціювання степеневих рядів.
4.Знакозмінні ряди. Ознака Лейбніца збіжності знакопереміжного ряду.
Згадані ознаки збіжності числових рядів відносились до рядів з додатніми членами. Розглянемо тепер ряди, частина членів яких додатня, а частина - від’ємна або рівна 0.
Якщо члени числового ряду мають різні знаки, то ряд називається знакозмінним.
Якщо
два підряд члени ряду мають різні
знаки, то знакозмінний ряд називається
знакопереміжним. Він має вигляд
![]() .
.
Числа
![]() - додатні. На питання про збіжність або
розбіжність такого ряду дає відповідь
ознака Лейбніца.
- додатні. На питання про збіжність або
розбіжність такого ряду дає відповідь
ознака Лейбніца.
Ознака
Лейбніца.
Якщо із зростанням номера
n
члени
ряду
за абсолютною величиною спадають, а
загальний член
![]() прямує до нуля при
прямує до нуля при
![]() ,
тобто
,
тобто
![]() то знакозмінний ряд збігається.
то знакозмінний ряд збігається.
Приклад. Дослідити збіжність ряду
![]() .
.
Розв’язування. Абсолютні величини членів знакозмінного ряду спадають:
![]() і
границя загального члена рівна 0,
тобто
і
границя загального члена рівна 0,
тобто
![]()
Обидві умови ознаки Лейбніца виконуються , тому заданий ряд збігається.
5. Абсолютна та умовна збіжність ряду.
Розглянемо
знакозмінний ряд, у якому члени з
додатніми і від’ємними
знаками не обов’язково
чергуються. Позначимо такий ряд
де
![]() числа як додатні, так і від’ємні.
Складаємо ряд з абсолютних величин
його членів:
числа як додатні, так і від’ємні.
Складаємо ряд з абсолютних величин
його членів:
![]() .
.
Якщо ряд з абсолютних величин збігається, то знакозмінний ряд називається абсолютно збіжним. Якщо знакозмінний ряд збігається, а ряд, складений з абсолютних величин, розбігається, то знакозмінний ряд називається неабсолютно збіжним або умовно збіжним.
Приклад
1.
Дослідити збіжність ряду
![]()
Розв’язування.
Даний ряд називається рядом Лейбніца.
Оскільки
![]()
![]() то
даний ряд збігається (згідно з ознакою
Лейбніца).
то
даний ряд збігається (згідно з ознакою
Лейбніца).
Ряд,
складений із абсолютних величин
![]() є гармонічним, який, як відомо, розбіжний.
Отже, даний ряд є умовно збіжний.
є гармонічним, який, як відомо, розбіжний.
Отже, даний ряд є умовно збіжний.
Приклад 2. Дослідити збіжність ряду
![]() .
.
Розв’язування.
Складемо ряд з абсолютних величин
![]() . Він збігається як ряд нескінченно
спадної геометричної прогресії із
знаменником
. Він збігається як ряд нескінченно
спадної геометричної прогресії із
знаменником
![]() Отже заданий ряд збігається абсолютно.
Отже заданий ряд збігається абсолютно.
6.Степеневий ряд та його збіжність. Область збіжності степеневого ряду.
Ряд,
членами якого є функції змінної
х,
називається функціональним. Це ряд
вигляду
![]() .
.
Якщо х набуває будь-якого числового значення, то ряд називається числовим.
Сукупність
всіх значень змінної х,
при яких функціональний ряд збігається,
називається областю збіжності цього
ряду. Будемо розглядати ряди, областями
збіжності яких служать різні інтервали
осі
![]()
Якщо
для всякого значення
![]() із інтервалу
із інтервалу
![]() функціональний ряд збігається,то його
сума
функціональний ряд збігається,то його
сума![]() (1) Інакше кажучи, функція
в інтервалі ]а,b[
розкладається в ряд.
(1) Інакше кажучи, функція
в інтервалі ]а,b[
розкладається в ряд.
Степеневим
рядом
називається функціональний ряд вигляду
![]() , (2)
, (2)
де
![]() - постійні числа.
- постійні числа.
Іноді
розглядають степеневий ряд більш
загального вигляду:![]() , (3)
, (3)
де
![]() деяке постійне число.
деяке постійне число.
Останній
ряд (3) легко зводиться до попереднього
степеневого ряду (2), якщо перепозначити
![]()
Теорема
1 (без
доведення).
Степеневий ряд (2) абсолютно збігається
при значеннях
![]() які знаходяться в деякому інтервалі
які знаходяться в деякому інтервалі
![]() і розбігається при значеннях
зовні цього інтервалу. Цей інтервал
називається інтервалом збіжності
(областю збіжності), а число
і розбігається при значеннях
зовні цього інтервалу. Цей інтервал
називається інтервалом збіжності
(областю збіжності), а число![]() радіусом
збіжності ряду (2).
радіусом
збіжності ряду (2).
Теорема
2.
Якщо існує
![]() то
то
![]() .
.
Доведення.
Маємо
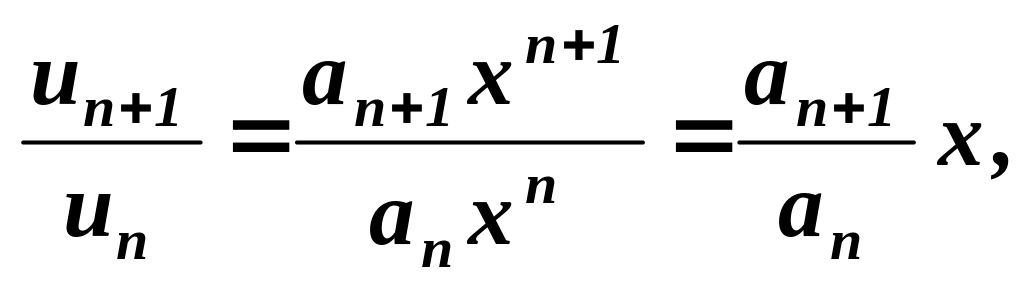 звідки
звідки
![]()
Згідно
ознаки Даламбера ряд (2) збігається,
якщо
![]() тобто
тобто
![]() і розбігається, якщо
і розбігається, якщо
![]() тобто якщо
тобто якщо
![]()
Отже,
степеневий ряд (2) збігається при тих
значеннях
![]() ,
для яких
,
для яких
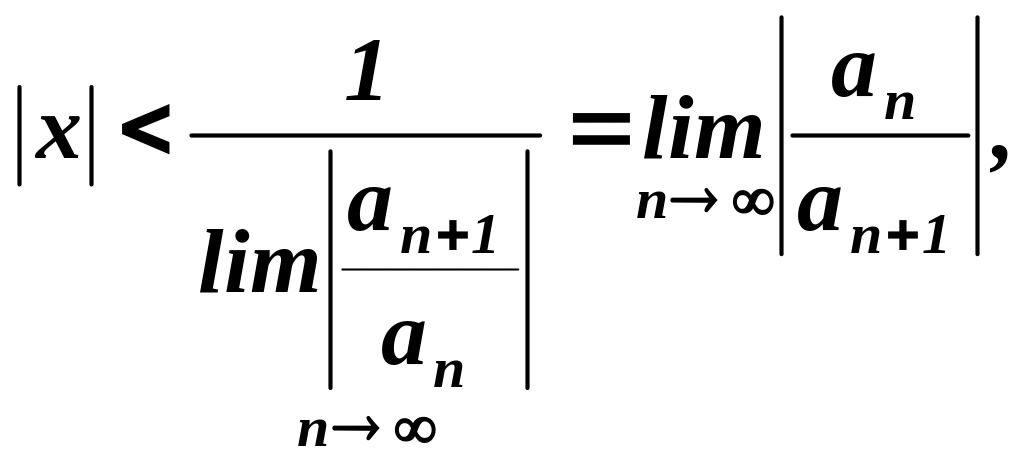 і
розбігається при тих значеннях
,
для яких
і
розбігається при тих значеннях
,
для яких
![]()
Таким
чином, для ряду (2)
![]()
При
![]() тобто при
тобто при
![]() степеневий ряд може збігатись, або
розбігатись.
степеневий ряд може збігатись, або
розбігатись.
Якщо
![]() то інтервал збіжності вироджується в
точку, а при
то інтервал збіжності вироджується в
точку, а при
![]() -
це вся числова вісь.
-
це вся числова вісь.
Приклад.
Знайти інтервал збіжності степеневого
ряду
![]() і дослідити збіжність на кінцях
інтервалу.
і дослідити збіжність на кінцях
інтервалу.
Розв’язування.
Тут
![]()
![]() .
.
Знаходимо радіус збіжності ряду
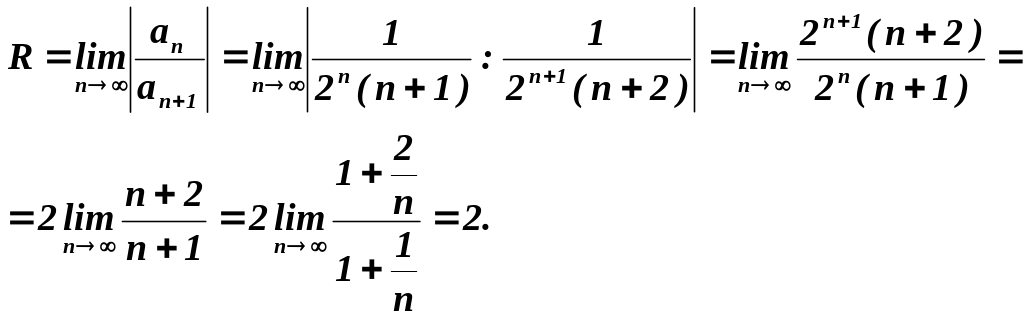
Отже
ряд збігається в інтервалі
![]() Щоб вирішити питання про збіжність
степеневого ряду на кінцях інтервалу,
покладемо спочатку
Щоб вирішити питання про збіжність
степеневого ряду на кінцях інтервалу,
покладемо спочатку
![]()
Отримаємо
гармонічний ряд
![]() який,
як відомо, розбігається.
який,
як відомо, розбігається.
При
![]() одержимо знакозмінний ряд Лейбніца:
одержимо знакозмінний ряд Лейбніца:
![]() який
збігається умовно (див. попередній
матеріал). Таким чином, степеневий ряд
збігається для
є
який
збігається умовно (див. попередній
матеріал). Таким чином, степеневий ряд
збігається для
є
![]()
