5. Восстановление непрерывного сигнала

При прохождении дискретизированного сигнала через восстанавливающий фильтр (рис.10) каждая дельта-функция породит на выходе соответствующим образом сдвинутую и масштабированную копию импульсной характеристики фильтра. Следовательно, выходной сигнал представляет собой сумму сдвинутых и умноженных на отсчеты сигнала копий импульсных характеристик фильтра.

Выражение для дискретизированного сигнала:

.

Импульсная характеристика идеального фильтра низких частот:

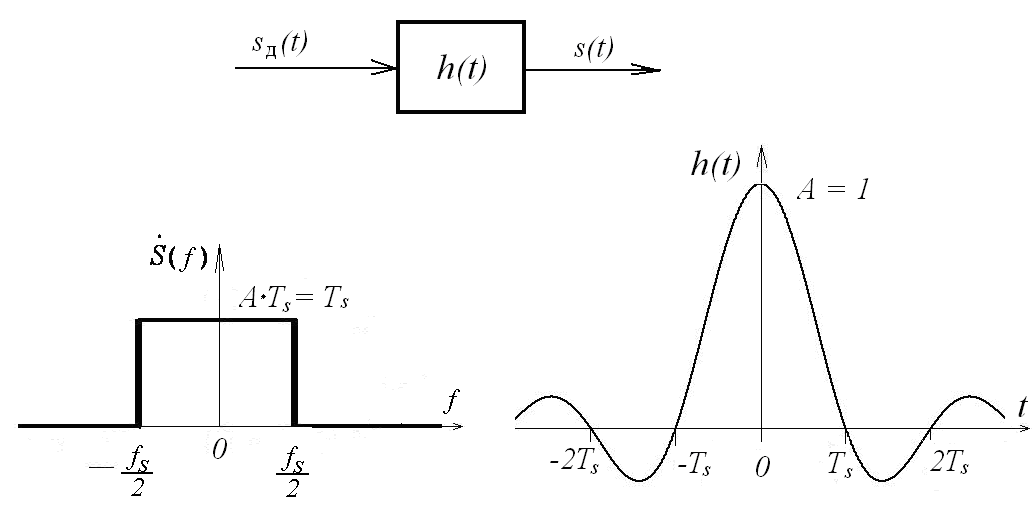
Рис.10 Амплитудно-частотная и импульсная характеристики

идеального восстанавливающего фильтра

Коэффициент передачи фильтра в полосе пропускания равен T_s (а не единице) с целью компенсации множителя 1/T_s в формуле расчета спектра дискретизированного сигнала. Импульсная характеристика фильтра рассчитывается согласно обратному преобразованию Фурье.

Следовательно, восстановленный сигнал:

Это выражение представляет собой разложение сигнала в ряд по системе функций , называемой базисом Котельникова, т.е. , что соответствует свертке: .

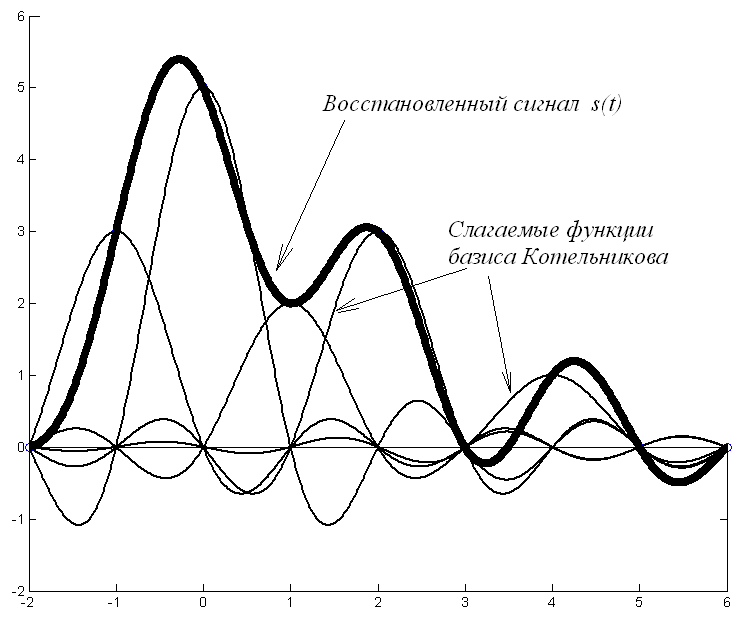
Пример восстановления непрерывного сигнала по дискретным отсчетам {0, 3, 5, 2, 3, 0, 1, 0, 0}, оцифрованных в моменты времени t_-2 … t₆ показан на рис.11. Сигнал бесконечен во времени, а его значения, за исключением исходных заданных, отличны от нуля. Колебания сигнала нигде не заканчиваются, несмотря на стремление амплитуды к нулю.

Рис.11 Пример восстановления непрерывного сигнала по дискретным отсчетам

6. Дискретизация полосовых сигналов

При полосовой дискретизации существенным является не максимальная частота сигнала, а ширина его спектра. Полосовая дискретизация учитывает эффект размножения спектра и позволяет снизить частоту семплирования.

Спектр непрерывного полосового сигнала, содержащего частоты от до , показан на рис.12а. При дискретизации с частотой согласно критерию Найквиста формируется частотный периодический спектр, показанный на рис.12б. Сигнал восстанавливается после предварительной фильтрации через фильтр нижних частот.

Рис.12 Спектры: а) - непрерывного сигнала, б), в) - дискретизированного сигнала при различных частотах семплирования

Однако для точного восстановления достаточно не иметь перекрытия сдвинутых копий спектра. По причине частотной узкополосности исходного сигнала возможен выбор частоты дискретизации, не удовлетворяющей критерию Найквиста, но обеспечивающей, тем не менее, отсутствие перекрытия спектров (один из вариантов показан на рис.12в). В таком случае сигнал должен восстанавливаться с помощью полосового фильтра.

При отсутствии наложения спектр находится между зеркальными копиями (рис.13). Следовательно, и .

Рис.13. Расположение копий спектра

Из этих неравенств следует: и . Таким образом, , т.е. частота семплирования ограничена снизу удвоенной шириной спектра.

При уменьшении частоты семплирования будет увеличиваться количество зеркальных копий, максимально возможное число которых равно: . Для всех целых значений k, не превышающих допустимое значение, можно определить диапазон возможных значений частоты семплирования: .

Аналогично: , , .

Например, для сигнала со средней частотой 40Гц и шириной полосы 10Гц справедливо: .

Для целочисленных значений k допустимые частоты дискретизации:

k=1: ,

k=2: ,

k=3: (рис.14).

При k=0 диапазон допустимой частоты дискретизации – от 90Гц до бесконечности.

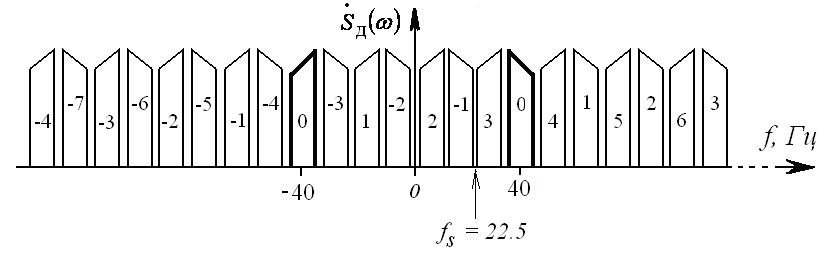
Рис.14 Спектр полосового сигнала

Допустимые частоты семплирования при полосовой дискретизации образуют ряд частотных диапазонов, разделенных неприемлемыми фрагментами. На рис.15 показан график допустимых частот дискретизации как функции переменной (параметр R определяет соотношение наибольшей частоты в сигнале к ширине спектра).

Рис.15 Графическое представление допустимых частот

семплирования при полосовой дискретизации

Для последнего примера R=4.5. Из графика следует, что наибольшее значение k=3, а минимально допустимая частота в 2,25 раза должна превышать ширину спектра, т.е. быть равной 22,5Гц.