Дискретизация сигналов Стр.13(13)

Дискретизация сигналов

Сигнал преобразуется из аналоговой формы в цифровую в ходе оцифровки, предполагающей дискретизацию во времени, квантование по уровню и кодирование.

1. Теоретические основы дискретизации

Дискретизация – это регистрация значений амплитуды непрерывного сигнала через определенные интервалы времени (рис.1а).

а) б)

Рис.1 Дискретизация сигнала

Исходный сигнал является непрерывной функцией времени, т.е. аналоговым. Измеренные значения амплитуды образуют набор дискретных значений сигнала, называемых отсчетами. Такое представление сигнала называют дискретным (рис.1б). Результатом дискретизации является сигнал в амплитудно-импульсной модуляции (pulse-amplitude modulation - PAM).

Количество замеров амплитуды в одну секунду называют частотой дискретизации или частотой выборки, частотой семплирования (англ. "sampling" – "выборка"). Частота дискретизации определяет разрешающую способность аналого-цифрового преобразования. Величина, обратная частоте дискретизации, называется периодом или шагом дискретизации (семплирования).

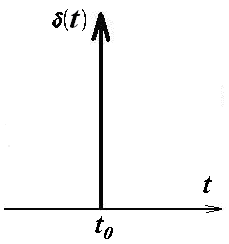
Для анализа дискретизации используется специальная теоретическая функция – "дельта-функция" (функция Дирака), которая представляет собой бесконечно узкий импульс с бесконечной амплитудой, расположенной при нулевом значении аргумента (рис.2).

	Размерность дельта-функции обратна размерности ее аргумента, например, дельта-функция времени имеет размерность 1/с.
Рис.2 График дельта-функции

Свойства дельта-функции:

а) Площадь импульса равна единице, т.е. .

б) Фильтрация – если дельта-функция присутствует под интегралом в качестве множителя, то результат интегрирования равен значению остального подынтегрального выражения в той точке, где сосредоточен дельта-импульс: .

в) Спектр дельта-функции равен единице: .

г) Согласно обратному преобразованию Фурье: .

При использовании дельта-функций непрерывному сигналу ставится в соответствие дискретизированный сигнал, который выглядит как последовательность дельта-функций, взвешенных значениями соответствующих амплитуд, т.е. отсчетов. Один из вариантов теоретического представления дискретизации поясняется на рис.3.

а) Непрерывный сигнал – функция от времени

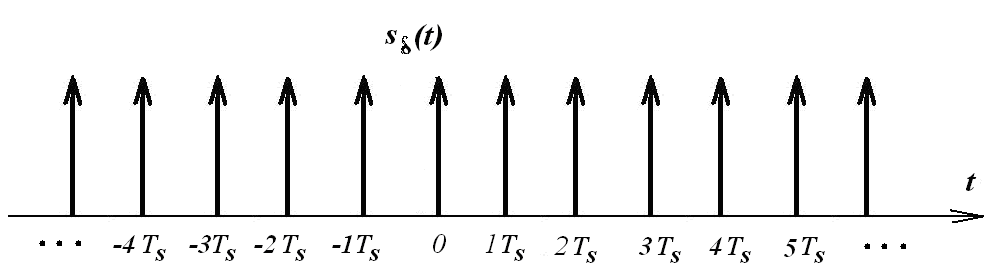
б) Сигнал из дельта-функций

в) Дискретизированный сигнал – ряд импульсов:

При T_s=1: , что аналогично записи

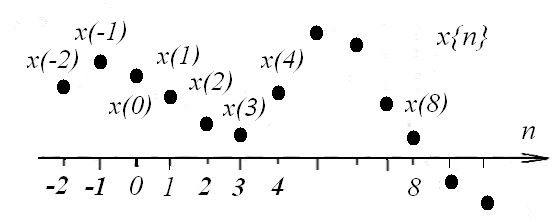
г) Дискретные отсчеты – последовательность чисел

Рис.3 Форма сигналов при дискретизации

Например, запись

или соответствует дискретизации сигнала, показанного на рис.4 (при единичном шаге).

Рис.4 Пример дискретизации

2. Неопределенность дискретизации.

Дискретное представление сигнала связано с частичной потерей информации об исходном сигнале в интервалах между измеренными значениями. Качество дискретизации оценивается способностью сохранить в последовательности отсчетов информацию об исходном сигнале, и зависит, в первую очередь, от частоты дискретизации. Но, в любом случае, дискретизации свойственна неопределенность, заключающаяся в том, что никакая последовательность отсчетов не может однозначно представить один и только один непрерывный сигнал без дополнительной информации. Одна и та же дискретная последовательность отсчетов может быть сопоставлена бесконечному количеству разных непрерывных сигналов.

Например, в результате дискретизации непрерывного синусоидального сигнала с частотой (с шагом ) сформированы отсчеты в моменты времени , , …, которые имеют значения:

Момент времени		Номер отсчета	Значение сигнала	Значение отсчета
t0	0Ts	0
t1	1Ts	1
t2	2Ts	2
t3	3Ts	3
		…	…	…
tn-1	(n-1)Ts	(n-1)
tn	nTs	n
tn+1	(n+1)Ts	(n+1)
		…	…	…

Согласно такому представлению первый период синусоидального сигнала начинается с отсчета с номером 0, второй – с номером n, третий – с номером 2n и т.д. Значения сигнала в эти моменты одинаковы, но разнесены на интервал, кратный радиан, т.к. в синусоиде , где m – любое целое число. Тогда

.

Значение m можно выбрать кратным значению n , т.е. , где k – любое положительное или отрицательное число:

.

Таким образом, .

Следовательно, множители и дают одинаковый результат. Дискретизация на частоте формирует последовательность цифровых отсчетов, представляющих не только синусоиду частотой , но и синусоиды с частотами, кратными , т.е. и т.д.

Например, отсчеты, полученные при дискретизации синусоиды на частоте , могут быть получены в случае , , , т.к. (рис.5). Такой сигнал называется алиас (alias), т.е. псевдоним, а эффект - алиасинг (aliasing), т.е. наложение частот.

Рис.5 Дискретизация сигналов 7Гц и 3Гц на частоте 4Гц