1.3 Множення на дробові числа
Часто на уроках математики завдавало складнощів множення на дроби. Розглянувши наступні способи труднощів стане менше.
Множення на щоб усно помножити число на , додають до першого множника його половину. Наприклад:
34∙ =34+17=51;
23∙
=23+
=
(або 34,5)
8
Щоб усно помножити число на , додають до його множника його четверту частину. Наприклад:
48∙ =48+12=60;
68∙
=58+
=
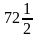(або 72,5)
Щоб
помножити перший множник на
,
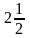до подвоєного числа додають половину
множника. Наприклад:
18∙ =36+9=45;
39∙
=78+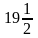
=
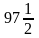(або 97,5)
Інший спосіб полягає в тому щоб множник помножити на 5 і поділити навпіл. Наприклад: 18∙ =90:2=45.
Щоб
усно помножити на
,
дане число множать на
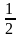і ділять навпіл. Наприклад:
30∙
=
=
(або
22,5).
1.4 Швидке ділення.
Швидко ділити так само важливо як і швидко множити
Ділення на 4 і на 8.
Щоб усно поділити число на 4, його двічі ділять пополам. Наприклад:
76:4=38:2=19;
256:4=118:2=59.
Щоб усно поділити число на 8, його тричі ділять пополам. Наприклад:
464:8=232:4=116:2=38;
516:8=258:4=129:2=64,5.
9
Щоб
усно поділити число на 5, відділяють
комою в подвоєному числі останню цифру.
Наприклад: 68:5=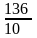
=13,6;
237:5=47,5.
Щоб усно поділити число на , ділять подвоєне число на три. Наприклад:
36: =72:3=24;
53:
=106:3=
Щоб усно поділити число на 15, ділять подвоєне число на 30. наприклад:
240:15=480:30=16;
462:15=924:30=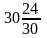
=30,8.
1.5 Ознаки подільності.
Важливо знати ознаки подільності. Частково їх вивчаються у школі на уроках
математики та цього надто мало. Я протпоную розглянути деякі з них
Ознаки подільності
Ознака подільності на 10
На 10 діляться всі ті і лише ті числа, які закінчуються нулями.
Ознака подільності на 2 і на 5
На 2 або на 5 діляться ті і лише ті числа, у яких остання цифра зображає число, що ділиться відповідно на 2 або на 5.
Ознака подільності на 3 і на 9
На 3 або на 9 діляться ті і лише ті числа, у яких сума цифр ділиться відповідно на 3 або на 9.
Ознака подільності на 4 і на 25
На 4 або на 25 діляться ті і лише ті числа, які закінчуються двома нулями, або у яких дві останні цифри зображають число, що ділиться відповідно на 4 або на
25. 10
Ознака подільності на 8 і на 125
На 8 або на 125 діляться ті і лише ті числа, які закінчуються трьома нулями, а також ті, у яких три останні цифри зображають число, що ділиться відповідно на 8 або на 125.
Ознака подільності на 7, 11 і 13
На 7, 11 і 13 діляться ті і лише ті числа, у яких різниця між числом, зображеним трьома останніми цифрами, і числом, зображеним рештою цифр (або навпаки), ділиться відповідно на 7, на 11 або на 13.
Ознака подільності на 11
На 11 діляться ті і лише ті числа, у яких різниця між сумою цифр, що стоять на парних місцях, і сумою решти цифр ділиться на 11.
Ознаки подільності на 6, 12, 18, 24 і т. д.
На 6 діляться ті і лише ті числа, які діляться на 2 і на 3.
Ознака подільності на 17
Число ділиться на 17 тоді і тільки тоді, коли число його десятків, складене із збільшеним в 12 разів числом одиниць, кратно 17 (наприклад, 29053 → 2905 +36 = 2941 → 294 +12 = 306 → 30 +72 = 102 → 10 +24 = 34 . Оскільки 34 ділиться на 17, то і 29053 ділиться на 17). Ознака не завжди зручний, але має певне значення в математиці. Є спосіб трохи простіше - число ділиться на 17 тоді і тільки тоді, коли різниця між числом його десятків і упятеренним числом одиниць кратна 17 (наприклад, 32952 → 3295-10 = 3285 → 328-25 = 303 → 30-15 = 15; оскільки 15 не ділиться на 17, то і 32952 не ділиться на 17) Після перевірки спосіб не діє.
Ознака подільності на 23
Число ділиться на 23 тоді і тільки тоді, коли число його сотень, складене з потроєною числом десятків і одиниць, кратно 23 (наприклад, 28 842 ділиться на 23, так як 288 + (3 * 42) = 414; продовжуємо: 4 + (3 * 14) = 46 - очевидно, ділиться на 23).
Ознака подільності на 99
11
Розіб'ємо число на групи по 2 цифри справа наліво (у самій лівій групі може бути одна цифра) і знайдемо суму цих груп, вважаючи їх двозначними числами. Ця сума ділиться на 99 тоді і тільки тоді, коли саме число ділиться на 99.
Ознака подільності на 101
Розіб'ємо число на групи по 2 цифри справа наліво (у самій лівій групі може бути одна цифра) і знайдемо алгебраїчну суму цих груп зі змінними знаками, вважаючи їх двозначними числами. Ця сума ділиться на 101 тоді і тільки тоді, коли саме число ділиться на 101. Наприклад, 590547 ділиться на 101, так як 59-05 +47 = 101 ділиться на 101.
Загальна ознака подільності чисел
Для того, щоб число N ділилося на d, необхідно і достатньо, щоб сума добутків цифр цього числа на остачі, які одержуються від ділення на d відповідних степенів десяти ділилася на d.