Теорема Коши о существовании и единственности решения задачи дифференциального уравнения первого порядка.
См. Степанова. Более адекватного доказательства я не нашел.
Метод последовательных приближений.
Пусть требуется найти
решение 
дифференциального
уравнения
(1) |
удовлетворяющее начальному условию
(2) |
Будем предполагать,
что в некотором прямоугольнике 
с
центром в точке 
для
уравнения (1) выполнены условия а) и б)
теоремы существования и единственности
решения задачи (1)-(2).
Решение задачи (1)-(2) может быть найдено методом последовательных приближений, который состоит в следующем.
Строим
последовательность 
функций,
определяемых рекуррентными соотношениями
(3) |
В качестве нулевого
приближения 
можно
взять любую функцию, непрерывную в
окрестности точки 
,
в частности 
—
начальное значение Коши (2). Можно
доказать, что при сделанных предположениях
относительно уравнения (1) последовательные
приближения
сходятся
к точному решению уравнения (1),
удовлетворяющему условию (2), в некотором
интервале
,
где
(4) |
Оценка погрешности,
получаемой при замене точного решения 
n-м
приближением 
,
даётся неравенством
(5) |
где 
.
Применяя метод последовательных
приближений, следует остановиться на
таком 
,
для которого 
не
превосходит допустимой погрешности.
Следствия из теоремы Коши.
Опять же Степанов.
Принцип сжатых отображений. Особые точки и особые решения.
Определение особого решения
Функция φ(x) называется особым решением дифференциального уравнения F(x,y,y') = 0, если единственность решения нарушается в каждой точке этой функции в области определения дифференциального уравнения. Геометрически это означает, что через каждую соответствующую точку (x0,y0) проходит более одной интегральной кривой с общей касательной. Примечание: Иногда используется более слабое определение особого решения, когда единственность решения нарушается лишь в некоторых точках. Особое решение дифференциального уравнения не описывается общим интегралом. Поэтому, оно не выводится из общего решения ни при каком значении постоянной C. Это можно проиллюстрировать следующим примером: Пусть требуется решить уравнение (y')2 − 4y = 0. Видно, что общее решение данного уравнения описывается функцией y = (x + C)2. Графически общее решение представляется в виде семейства парабол (Рисунок 1).
|
|
|
Рис.1 |
|
|
Кроме этого, функция y = 0 также удовлетворяет дифференциальному уравнению. Однако эта функция не содержится в общем решении! Поскольку через каждую точку прямой y = 0 проходит более одной интегральной кривой, то единственность решения на этой прямой нарушается, и, следовательно, данная прямая является особым решением дифференциального уравнения.
p-дискриминант
Одним из способов
нахождения особого решения является
исследование так
называемого p-дискриминантадифференциального
уравнения. Если функция F(x,y,y') и
ее частные производные 
, 
непрерывны
в области определения дифференциального
уравнения, то особое решение находится
из системы уравнений:
Уравнение ψ(x,y) = 0, которое получается при решении данной системы, называется p-дискриминантомдифференциального уравнения. Соответствующая кривая, определенная этим уравнением, называется p-дискриминантной кривой. После нахождения p-дискриминантной кривой необходимо проверить следующее:
Является ли p-дискриминант решением дифференциального уравнения?
Является ли p-дискриминант особым решением, то есть существуют ли другие интегральные кривые дифференциального уравнения, которые касаются p-дискриминантной кривой в каждой точке?
Это можно сделать следующим образом:
Сначала нужно найти решение дифференциального уравнения (обозначим его как y1);
Затем нужно записать условия касания кривой особого решения (обозначим его как y2) и семейства интегральных кривых общего решения y1 в произвольной точке x0:
Если данная система имеет решение в произвольной точке x0, то функция y2 будет являться особым решением. Особое решение обычно соответствует огибающей семейства интегральных кривых общего решения дифференциального уравнения.
Огибающая семейства интегральных кривых и C-дискриминант
Другой способ нахождения особого решения в виде огибающей семейства интегральных кривых основан на использовании C-дискриминанта. Пусть Φ(x,y,C) является общим решением дифференциального уравнения F(x,y,y') = 0. Графически уравнениеΦ(x,y,C) = 0 соответствует семейству интегральных кривых на плоскости xy. Если функция Φ(x,y,C) и ее частные производные непрерывны, то огибающая семейства интегральных кривых общего решения определяется системой уравнений:
Чтобы убедиться, что решение данной системы уравнений действительно является огибающей, можно воспользоваться методом, рассмотренным в предыдущем пункте.
Общий алгоритм нахождения особых точек
Более общий способ нахождения особых точек дифференциального уравнения основан на одновременном использовании p-дискриминанта и C-дискриминанта. Сначала мы определяем уравнения p-дискриминанта и C-дискриминанта:
ψp(x,y) = 0 − уравнение p-дискриминанта;
ψC(x,y) = 0 − уравнение C-дискриминанта;
Оказывается, что эти уравнения имеют определенную структуру. В общем случае, уравнение p-дискриминанта представляется в виде произведения трех функций:
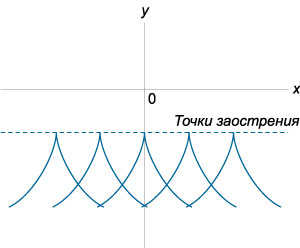
где E означает уравнение огибающей, T − уравнение точек прикосновения и C − уравнение точек заострения. Аналогично, уравнение C-дискриминанта также раскладывается на произведение трех функций:
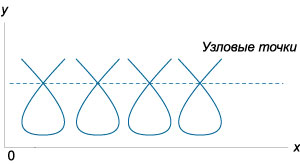
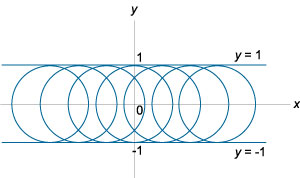
где E − уравнение огибающей, N − уравнение узловых точек, а C − уравнение точек заострения. Здесь мы имеем дело с новыми типами особых точек: C - точки заострения, T - точки прикосновения иN - узловые точки. Их вид в плоскости xy схематически представлен на рисунках 2-4.
|
|
|
Рис.2 |
|
Рис.3
|
|
|
|
Рис.4 |
|
Рис.5 |
Три типа особых точек из четырех, а именно: точки заострения, точки прикосновения и узловые точки, − являются внешними, то есть они не удовлетворяют дифференциальному уравнению и, поэтому, не являются особыми решениями дифференциального уравнения. Только уравнение огибающей будет являться особым решением. Поскольку огибающая входит в уравнения обоих дискриминантов в виде множителя в первой степени, то ее уравнение легко определяется из данной системы.