Список вопросов.

1. Определение дифференциального уравнения. Понятие общего решения и частного решения. 2. Уравнения с разделяющимися переменными. 3. Однородные уравнения и уравнения, приводящие к однородным. 4. Линейные уравнения первого порядка. 5. Уравнение Бернулли. 6. Уравнение Риккати. 7. Уравнения в полных дифференциалах. 8. Уравнения с интегрирующим множителем. 9. Теорема Коши о существовании и единственности решения задачи дифференциального уравнения первого порядка. 10. Метод последовательных приближений. 11. Следствия из теоремы Коши. 12. Принцип сжатых отображений. 13. Особые точки и особые решения. 14. Уравнения, не разрешенные относительно производной.

Определение дифференциального уравнения. Понятие общего решения и частного решения.

Дифференциальное уравнение – уравнение, связывающее независимую переменную x и y, y’, y’’,…,y⁽ⁿ⁾

Общий вид:

Решение ДУ – всякая функция , которая, при подстановке в ДУ, обращает ДУ в тождество.

При этом график функции называется интегральной кривой.

Общее решение уравнения это функция , удовлетворяющая следующим условиям:

1. C обращает в тождество

2. , удовлетворяет данным условиям, при этом - частное решение.

По Степанову:

Уравнения с разделяющимися переменными.

(*)

(*):

Получим

или при

Затем проверим

Пусть при x=b, тогда x=b – частное решение.

Пусть при y=a, тогда y=a – частное решение.

Однородные уравнения и уравнения, приводящие к однородным.

По Степанову:

Проверка уравнения на однородное

В исходное уравнение:  

вместо   подставляем  , вместо   подставляем  , производную не трогаем:

Буква лямбда – это некоторый абстрактный числовой параметр, дело не в самих лямбдах, и не в их значениях, а дело вот в чём:

Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.

Очевидно, что лямбды сразу сокращаются в показателе степени: Теперь в правой части выносим лямбду за скобки:

Обе части уравнения можно сократить на эту самую лямбду: В результате все лямбды исчезли как сон, как утренний туман, и мы получили исходное уравнение.

Вывод: Данное уравнение является однородным.

Приведение к уравнению с разделяющимися переменными

Однородное уравнение приводится к уравнению с разделяющимися переменными путем замены y=tx, где t-функция, зависящая от x.

Уравнения, приводимые к однородным

К однородным уравнениям первого порядка приводится уравнение вида:

Как определить, что дифференциальное уравнение приводится к однородному

Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы: a₁ x + b₁ y + c₁, a₂ x + b₂ y + c₂, и выполнить замену:

a₁ x + b₁ y + c₁ → t(a₁ x + b₁ y + c₁); a₂ x + b₂ y + c₂ → t(a₂ x + b₂ y + c₂)

Если после преобразований t сократится, то это уравнение приводится к однородному.

Решение дифференциального уравнения, приводящегося к однородному уравнению

Решаем систему уравнений:

Здесь возможны три случая:

1) Система имеет бесконечное множество решений (прямые a₁ x + b₁ y + c₁ = 0 и a₂ x + b₂ y + c₂ = 0совпадают). В этом случае

Тогда

Это простейший вид уравнения с разделяющимися переменными:

Его решение:

2) Система не имеет решений (прямые a₁ x + b₁ y + c₁ = 0 и a₂ x + b₂ y + c₂ = 0 параллельны). В этом случае a₁ b₂ – a₂ b₁ = 0;

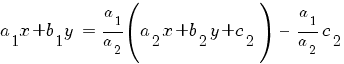
Это уравнение приводится к уравнению с разделяющимися переменными подстановкой  z = a₂ x + b₂ y + c₂.

3) Система имеет одно решение (прямые a₁ x + b₁ y + c₁ = 0 и a₂ x + b₂ y + c₂ = 0 пересекаются в одной точке). Обозначим это решение x₀, y₀. Тогда

Делаем подстановку x = t + x₀, y = u + y₀. Тогда dx = dt, dy = du,

или

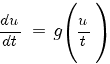
Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой u = zt, где z - функция от t.

Линейные уравнения первого порядка.

Решение линейного дифференциального уравнения с помощью интегрирующего множителя

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:

Существует три способа решения этого уравнения:

• метод интегрирующего множителя;

• метод введения двух функций (Бернулли);

• метод вариации постоянной (Лагранжа).

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.

Умножим исходное уравнение на интегрирующий множитель -

:

(1)

Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (1):

Интегрируем:

Умножаем на 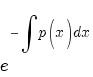   . Получаем общее решение линейного дифференциального уравнения первого порядка:

 

Метод введения двух функций (Бернулли)

Ищем решение исходного уравнения в виде произведения двух функций:

y = u·v

где u, v - функции от x. Дифференцируем:

y' = u'·v + u·v'

Подставляем в исходное уравнение:

Выносим u за скобки:

(1)

В качестве v возьмем любое, отличное от нуля, решение уравнения:

(2)

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx, делим на v:

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. Тогда

Потенцируем и опускаем знак модуля (это сводится к умножению на постоянную ±1)

Подставим в (1) учитывая, что согласно (2) выражение в скобках равно нулю:

Отсюда

Интегрируем

Окончательно находим:

 

Метод вариации постоянной (Лагранжа)

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx, делим на y:

Интегрируем:

Интеграл по y - табличный:

Тогда

Потенцируем:

Заменим постоянную e^C на C и уберем знак модуля, что сводится к умножению на постоянную ±1, которую включим в C:

(1)

Теперь считаем, что постоянная C является функцией от x:

Находим производную:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в исходное уравнение:

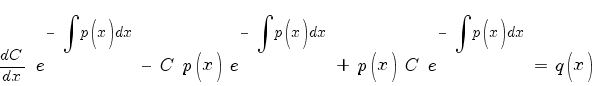
Два члена сокращаются. Отсюда

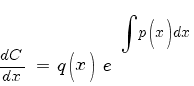
Интегрируем:

Где C₁ - постоянная интегрирования. Подставляем в (1):

Заменим постоянную C₁ на C. В результате получаем общее решение линейного дифференциального уравнения первого порядка:

Уравнение Бернулли.

Дифференциальное уравнение Бернулли – это уравнение вида 

 

Решение дифференциального уравнения Бернулли приведением к линейному уравнению

Исходное уравнение:

(1)

Разделим на yⁿ. При y ≠ 0 имеем

Это уравнение сводится к линейному с помощью замены переменной:

По правилу дифференцирования сложной функции

Подставляем:

Или:

Это линейное относительно z дифференциальное уравнение. После его решения следует рассмотреть случай y = 0. При n > 0, y = 0 также является решением уравнения и должно входить в ответ.

 

Решение методом Бернулли

Рассматриваемое уравнение можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:

где u, v - функции от x. Дифференцируем:

Подставляем в исходное уравнение (1):

(2)

В качестве v возьмем любое, отличное от нуля, решение уравнения:

(3)

Уравнение (3) - это уравнение с разделяющимися переменными. После того, как мы нашли его частное решение v = v(x), подставляем его в (2). Поскольку оно удовлетворяет уравнению (3), то выражение в круглых скобках обращается в нуль. Получаем:

Это также уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv.

Уравнение Риккати.

В Степанове оказалось очень много и сложно, поэтому из него не стал приводить.

Дифференциальное уравнение Риккати – это уравнение вида 

Общее решение этого уравнения можно получить только в некоторых частных случаях.

 

Решение дифференциального уравнения Риккати при известном частном решении

Пусть известно частное решение y₁(x) уравнения Риккати:

Тогда подстановкой y = y₁ + u такое уравнение приводится к уравнению Бернулли:

Или:

Или:

Это уравнение Бернулли с n = 2.

 

Свойства уравнения Риккати

Не меняет вид уравнения:

Произвольное преобразование независимого переменного:

x = φ(x₁)

Произвольное дробно-линейное преобразование зависимого переменного:

При таких подстановках уравнение также является уравнением Риккати, но с другими функциямиp, q, r.

 

Общее решение уравнения Риккати есть дробно-линейная функция от произвольной постоянной:

 

И наоборот если общее решение уравнения есть дробно-линейная функция от произвольной постоянной, то соответствующее уравнение есть уравнение Риккати.

 

Упрощение уравнение Риккати

Подстановкой:

где А - постоянная, уравнение Риккати приводится к виду:

где:

 

Далее, подстановкой:

оно приводится к виду:

где:

 

Упрощенное уравнение Риккати

Упрощенное уравнение Риккати - это уравнение вида:

(1)

где A, B - постоянные. Оно интегрируется при

где n = ±1, ±2, ±3,… - целое. Сделаем подстановку:

Подставляем в (1):

Умножаем на x²:

(2)

Но:

Подставляем в (2):

Или:

(3)

где:

Уравнение (3) интегрируется при   . Для этого разделим его на u² и перепишем в виде:

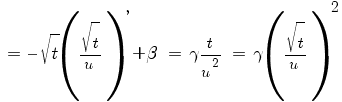
Или:

Это уравнение с разделяющимися переменными. Оно легко интегрируется.

При   уравнение (3) можно преобразовать двумя путями:

1. Подстановкой  , где  , оно преобразуется к виду:

2. Подстановкой  , где  , оно преобразуется к виду:

Таким образом, при  , где ν - целое число, ряд подстановок приводит к полному решению.

Уравнения в полных дифференциалах.

Дифференциальные уравнения первого порядка в полных дифференциалах – это уравнения вида 

 

Если выполняется условие:

(1)

то выражение:

является дифференциалом некоторой функции:

Тогда:

(2)

Исходное уравнение:

(3)

принимает вид:

dU = 0

Отсюда получаем его интеграл:

U = C

 

Как распознать дифференциальное уравнение в полных дифференциалах

Для того чтобы определить, что уравнение является уравнением в полных дифференциалах, нужно проверить выполнение соотношения (1). Поскольку вычисление производной занимает некоторое время, то сначала желательно проверить, не принадлежит ли уравнение одному из рассмотренному выше типов.

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:

du ± dv = d(u ± v)

v du + u dv = d(uv)

В этих формулах u и v - произвольные выражения, составленные из любых комбинаций переменных.

Метод последовательного интегрирования

Проинтегрируем первое уравнение (2):

где φ - функция от y.

Подставляем во второе уравнение (2):

Отсюда:

Интегрируя находим φ и, тем самым, U.

Метод прямого интегрирования

Функцию U, определяемую соотношением:

Можно найти непосредственным интегрированием:

где интегрирование выполняется по любой кривой, принадлежащей области существования p и q, соединяющей произвольную точку (x₀, y₀) и точку (x, y). После интегрирования члены, содержащиеx₀ и y₀ включают в постоянную C.

Для интегрирования этим методом нужно представить уравнение кривой, соединяющей точки (x₀, y₀) и (x, y) в параметрическом виде:

x₁ = s(t);    y₁ = r(t);

x₀ = s(t₀);    y₀ = r(t₀);

x = s(t₁);    y = r(t₁);

и интегрировать по t от t₀ до t₁.

Наиболее просто выполняется интегрирование по отрезку, соединяющем точки (x₀, y₀) и (x, y). В этом случае:

x₁ = x₀ + (x - x₀)t;    y₁ = y₀ + (y - y₀)t;

t₀ = 0; t₁ = 1

dx₁ = (x - x₀)dt;    dy₁ = (y - y₀)dt

После подстановки, получается интеграл по t от 0 до 1.

Данный способ, однако, приводит к довольно громоздким вычислениям, поэтому применять его не стоит.