
- •Новороссийск 2013
- •Числовая последовательность, предел последовательности
- •Функции
- •Ограниченная функция. Если существует такое число m, что . Например, функции
- •Квадратный трехчлен
- •4.1 Определение производной
- •2.2 Основные правила дифференцирования
- •Производная функции, заданной неявно
- •Правило Лопиталя для нахождения предела функции.
- •Производные высших порядков
- •2.4 Исследование функций План полного исследования функции:
- •Примеры исследования функции:
- •1.Основные понятия.
- •Упражнения
- •Интегрально исчисление
- •3.1 Неопределенный интеграл
- •1 Способ. Тригонометрическая подстановка.
- •3 Способ. Метод неопределенных коэффициентов.
- •3 .2 Определенный интеграл
- •3.2.1 Понятие определенного интеграла и его свойства
- •Тейлор (1685-1731) – английский математик
- •§9. Разложение функций в степенные ряды.
- •§10. Некоторые приложения степенных рядов.
§9. Разложение функций в степенные ряды.
I.
Непосредственное вычисление
![]()
II. Использование известных разложений (§8), действий с рядами, алгебраических формул,
единственности разложения, сдвига центра.
Примеры.
1)![]()
{
![]() }
}
2)
![]() {
{
![]()
![]()
![]() }
}
III. Почленное интегрирование рядов.
Пример.
Разложить в ряд Маклорена функцию
![]()
{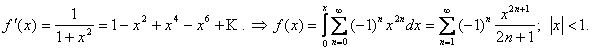 }
}
§10. Некоторые приложения степенных рядов.
Приближенные вычисления.
Пример.
Найти значение
![]() с точностью 0.001.
с точностью 0.001.
{![]() Так как это знакочередующийся ряд, то
его остаток меньше первого отброшенного
члена (гл.1,§11). Следовательно,
Так как это знакочередующийся ряд, то
его остаток меньше первого отброшенного
члена (гл.1,§11). Следовательно,![]() (с точностью 0.001).}
(с точностью 0.001).}
2. Интегрирование с помощью рядов.
Пример.
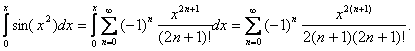
3. Решение дифференциальных уравнений.
Примеры. 1. Найти четыре первых члена разложения в ряд Тейлора решения дифференциального
уравнения:
![]()
{ Вычислим производные в т. х0=1:

![]() }
}
2*.
Решить уравнение:
![]()
{Будем
искать решение в виде степенного ряда:
![]()
Тогда
![]() Подставляя
данные выражения в уравнение, имеем:
Подставляя
данные выражения в уравнение, имеем:
![]() или
или
![]()
В силу начальных условий: а0 = 0, а1 = 1. Сравнивая коэффициенты при одинаковых степенях,
получим:
![]() Отсюда :
Отсюда :
![]() и
и
![]() }
}
