Московский государственный технический университет

имени Н. Э. Баумана

Домашнее задание

по курсу «Теория управления»

Вариант №3

Выполнил: Королева А.А.

Группа: АК2-91

Реутов, 2012 г.

1. Постановка задачи и исходные данные

1.1 Постановка задачи

1. Составить математическую модель пространственного движения КА вокруг центра масс (относительно ОСК).

2. Выбрать исполнительные органы – маховики для обеспечения стабилизации КА и разворота на заданные углы.

3. Провести моделирование режима разворота КА на заданный угол для диагонального и недиагонального тензора инерции. Рассмотреть влияние перекрестных связей на процесс разворота КА.

1.2 Исходные данные

Где Н – высота орбиты

i – угол наклонения орбиты

m – масса спутника

Jx, Jx, Jy, Jxy, Jyz, Jxz – компоненты тензора инерции

Система поворотов – ракетная

Задание кинематики – уравнения Пуассона

T – период обращения КА

h = 0,01 с – шаг интегрирования

R₀ = 6370 км – радиус орбиты

m = 3.958*10¹⁴ 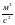– гравитационная постоянная Земли

Начальные значения: - углов

- угловых скоростей

2. Математическая модель пространственного движения ка вокруг центра масс.

Динамика вращательных движений относительно центра масс в соответствии с основной теоремой механики об изменении кинетического момента описывается векторным уравнением

- в инерциальных осях

(1)

где H – вектор кинетического момента КЛА,

М – главный момент внешних сил

- в связанных осях

(2)

,где - гироскопический момент.

В проекциях на связанные оси это уравнение выглядит следующим образом:

(3)

Проекции вектора кинетического момента КЛА на связанные оси

(4)

Подставив (4) в (3) получим следующую систему уравнений:

(5)

Считаем, что внутренние возмущающие моменты от сил Кориолиса малы (полагаем, что в задаче не происходит существенного изменения распределения масс). В таком случае можно упростить выражение (5) и получить следующую систему уравнений:

(6)

В случае, если тензор инерции диагональный, то для него будут справедлива следующая система уравнений:

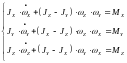(7)

Определяем производные угловых скоростей (динамические соотношения):

Запишем уравнение Пуассона

где А – матрица направляющих косинусов

- кососимметрическая матрица, составленная из проекций вектора угловой скорости на связанные оси координат

(11)

(12)

(13)

Подставляем (11) и (13) в (9) и раскрываем это уравнение, получим:

(14)

Для решения системы (14) достаточно будет шести уравнений.

Получаем математическую модель пространственного движения КА вокруг центра масс:

(15)

Другие элементы матрицы направляющих косинусов можно определить из соотношений:

(16)

Интегрируя численным методом Эйлера систему (15), вычисляем значения углов и угловых скоростей

, где