Примеры решения задач

Задача 12

Маховое колесо, имеющее момент инерции 245 кг∙м², вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.

Решение

При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.

ω ₀ = 2 π ν₀, ω = 0,

0 = 2 π ν₀ - ε t,

отсюда ε = .

Это ускорение обусловлено действием момента сил трения

M_тр = I ε = .

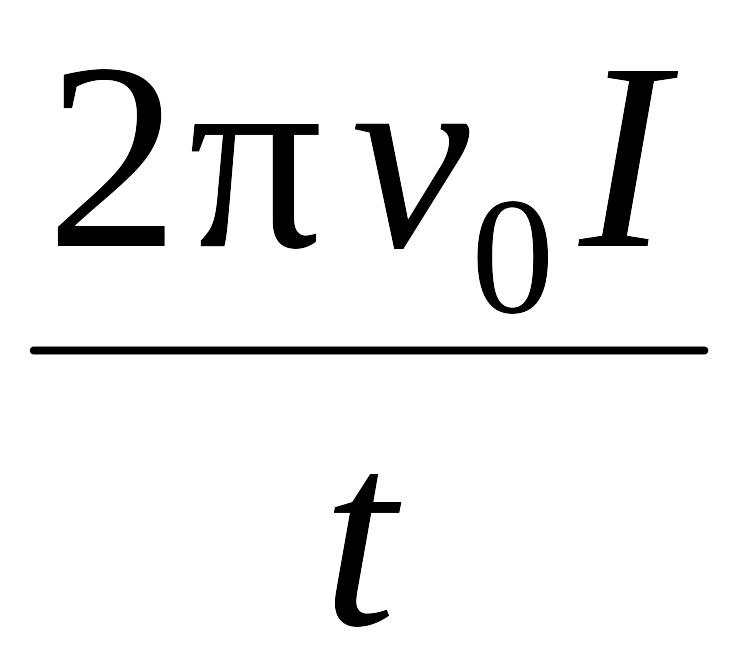Полный угол поворота при равнозамедленном движении находится из соотношения:

φ = ω₀ t- ,

φ =2π N, ω ₀ = 2 π ν₀, ε = .

Перепишем соотношения для угла в виде:

2π N = 2 π ν₀ t - = 2 π ν₀ t - = .

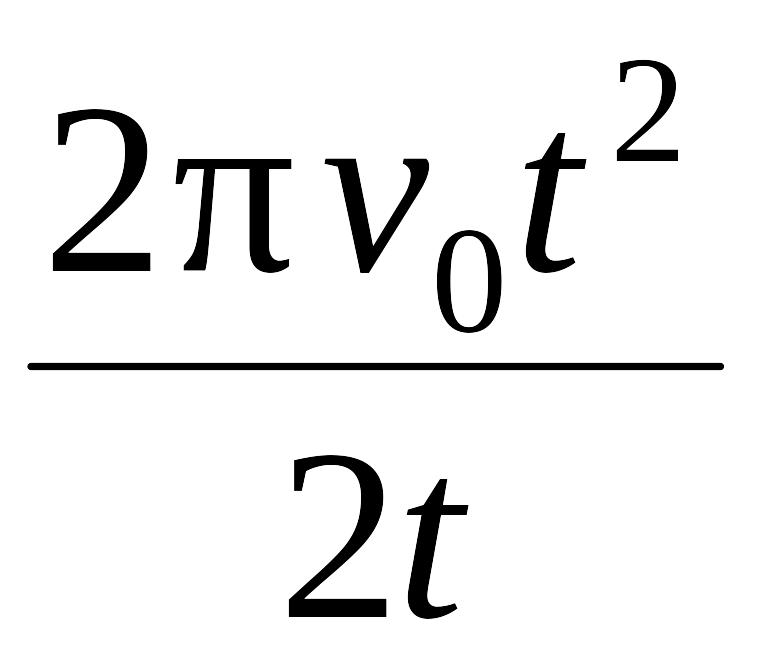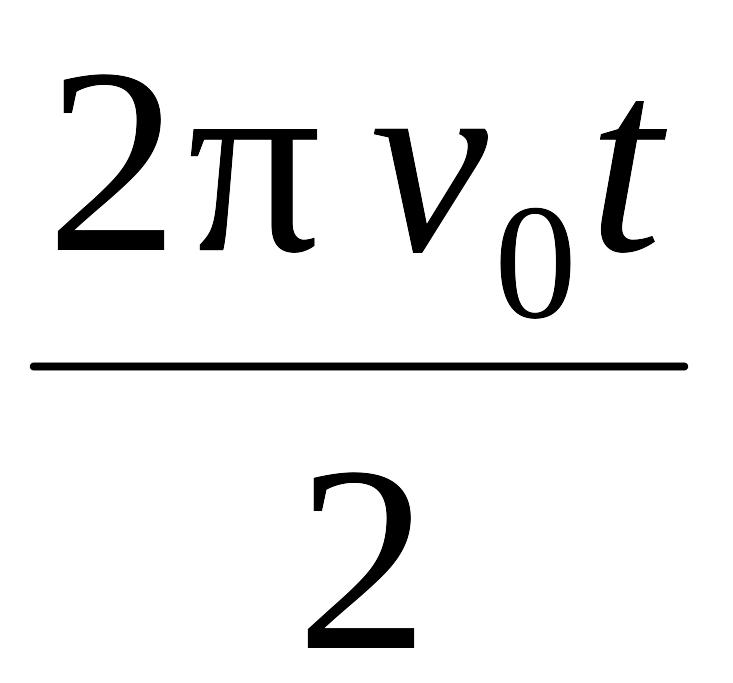Для нахождения числа оборотов получим:

N = .

Подставив числовые значения, найдём:

M_тр = 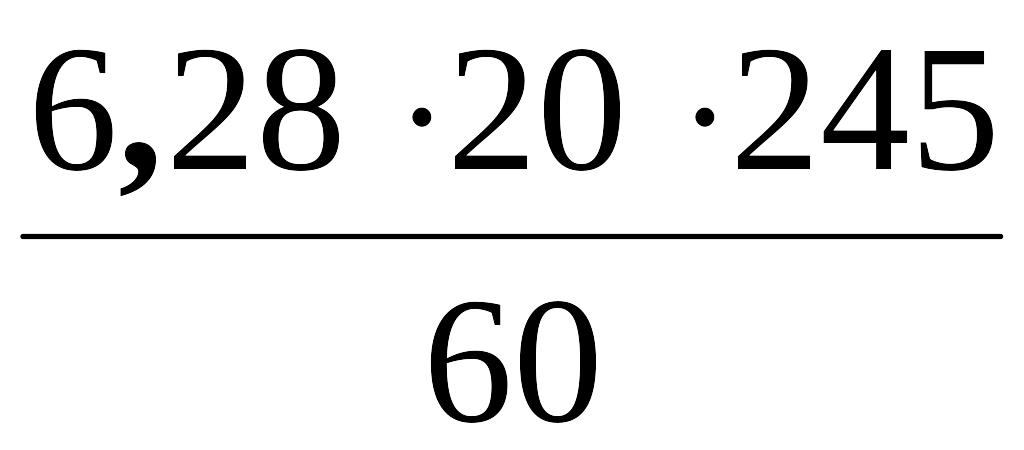= 506 Нм,

N = 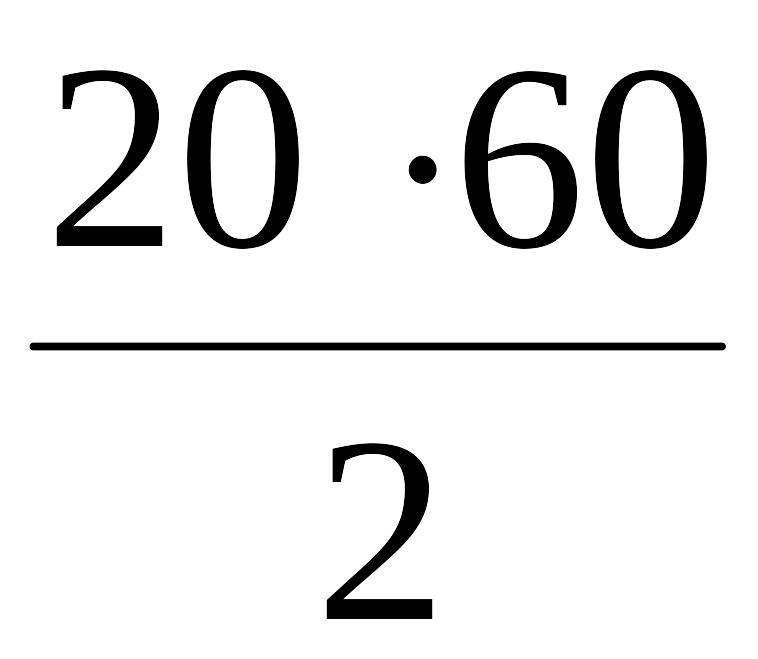= 600 об.

Задача 13

На барабан радиусом R = 20 см, момент инерции которого равен I = 0,1 кг∙м², намотан шнур, к которому привязан груз массой m = 0,5 кг. До начала вращения высота груза над полом равна h₁ = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.

Решение

Н а груз действует сила тяжести mg и сила натяжения шнура Т. Уравнение поступательного движения груза ma = mg – T.

Барабан вращается вокруг неподвижной оси. Его уравнение движения M = I ε,

где М – момент силы натяжения шнура, М = TR, I – момент инерции барабана,

ε = – его угловое ускорение.

TR = I .

Выражаем отсюда силу натяжения шнура:

T = I (10)

и подставляем ее в уравнение движения груза:

mg = a(m + ) = am(1 + ).

Получаем ускорение груза:

a = 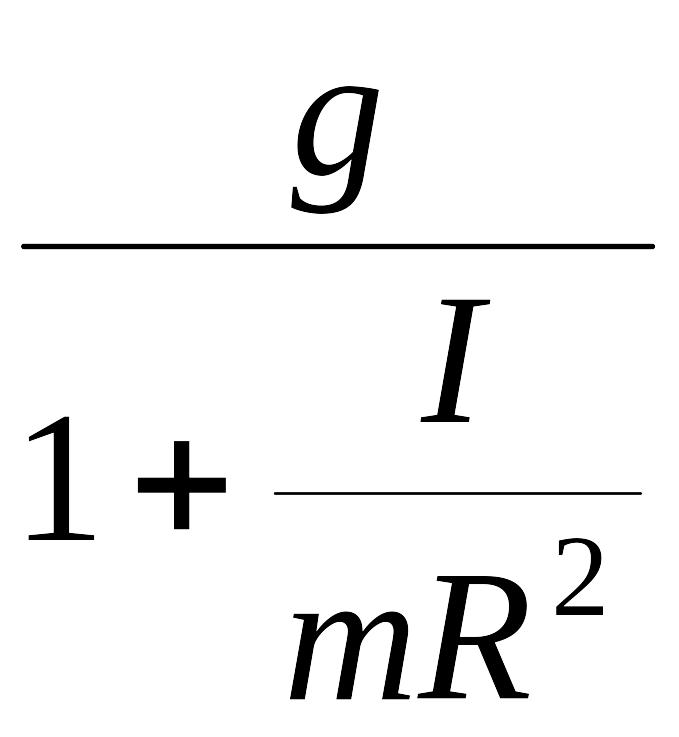. (11)

Время движения груза можно найти из уравнения:

h₁ = ,

t = = .

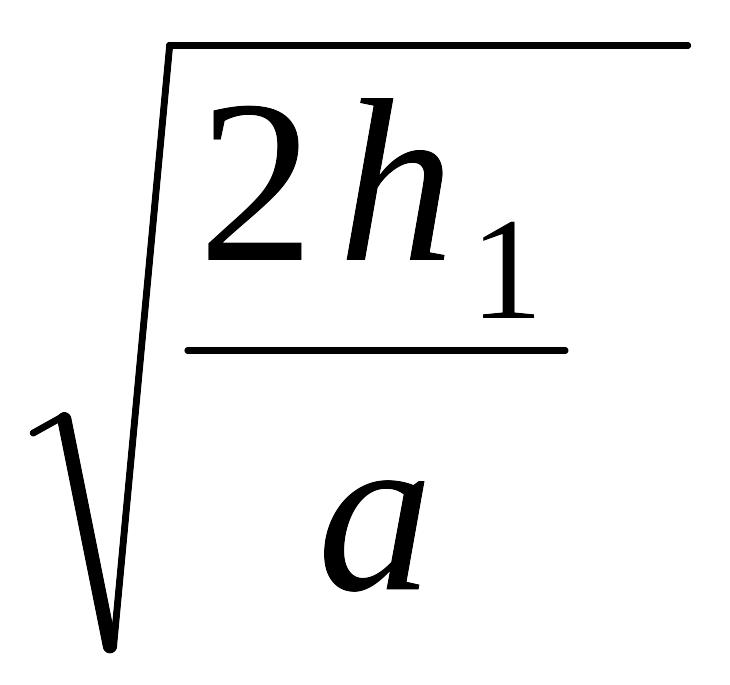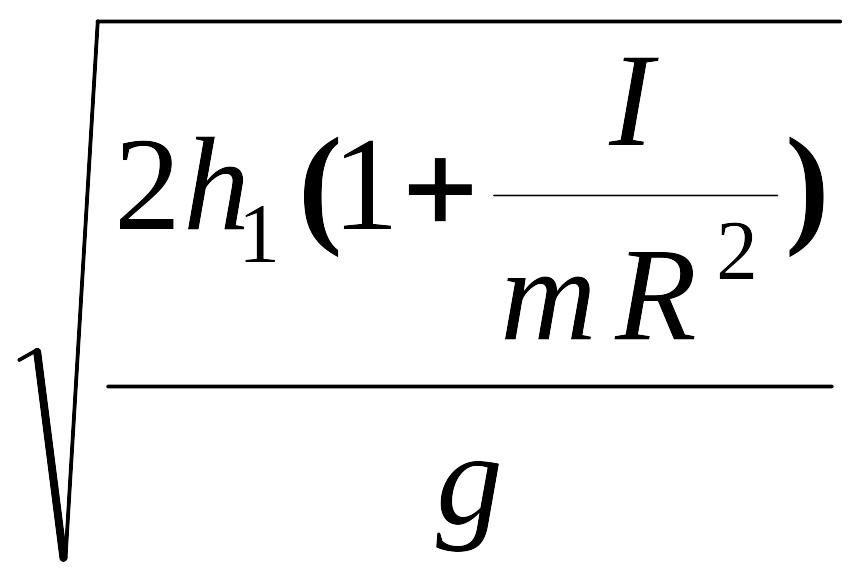В момент удара о пол груз имел скорость:

υ = at = .

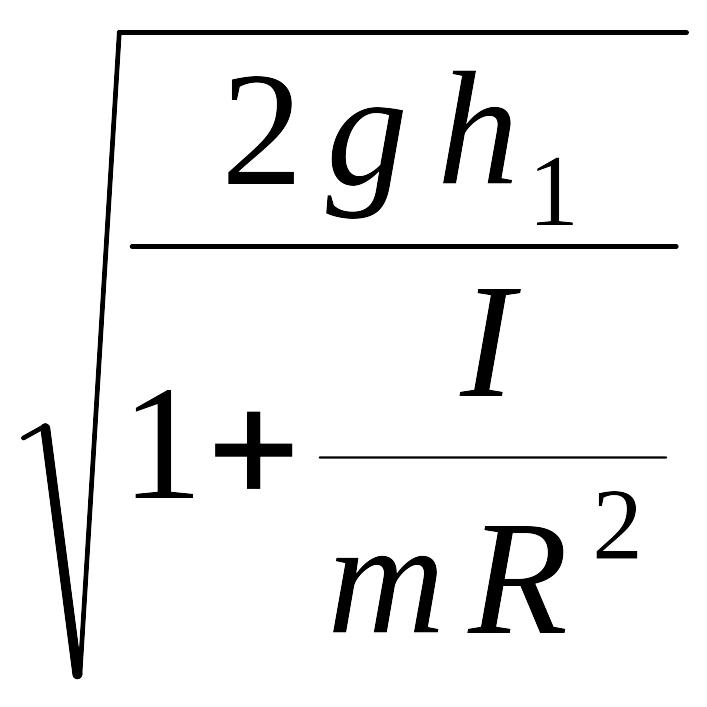Следовательно, его кинетическая энергия:

E_k = = .

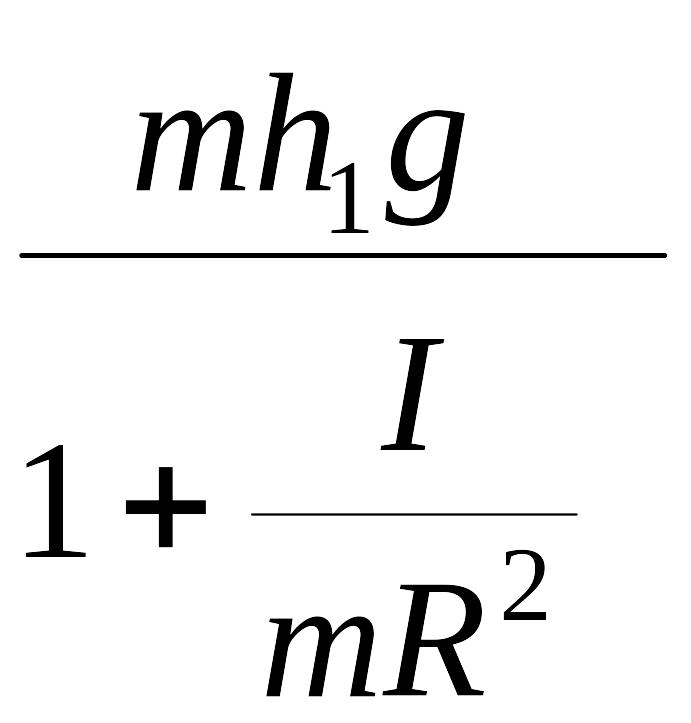Подставив выражение для ускорения (11) в формулу (10), получим:

T = = .

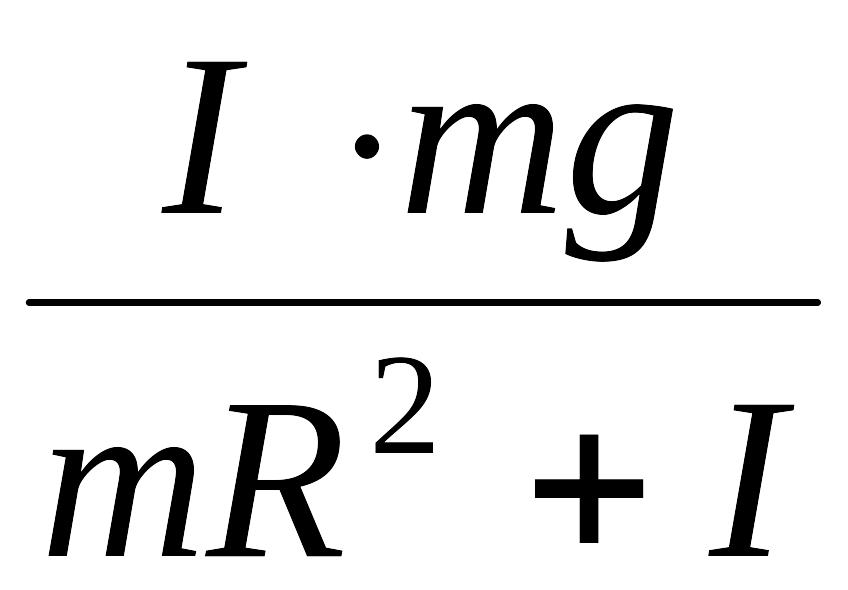Подставив числовые значения, определим искомые величины:

t = 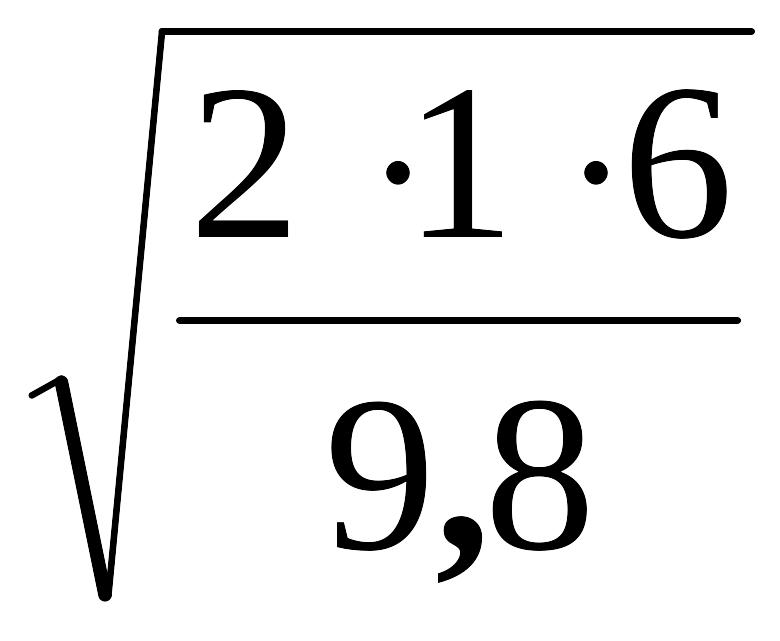= 1,1 c,

E_k = 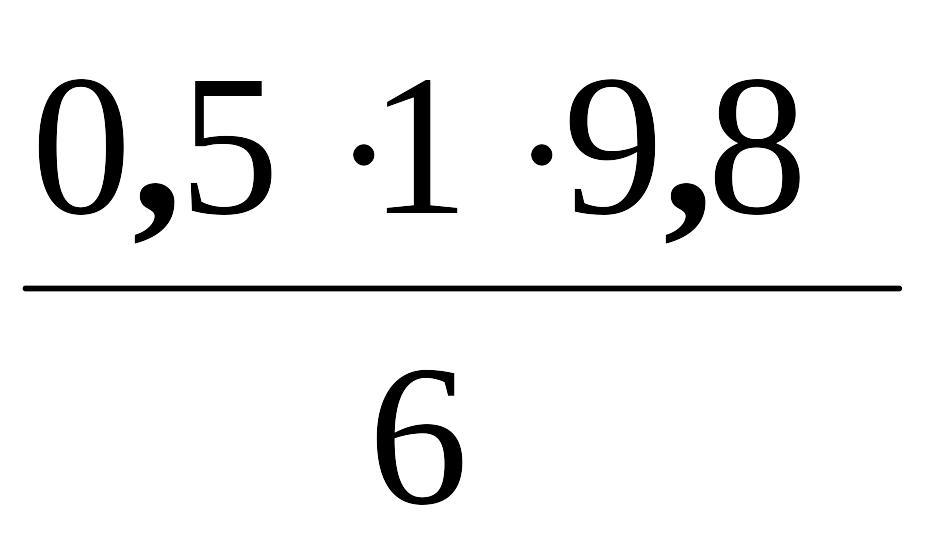= 0,82 Дж,

T = 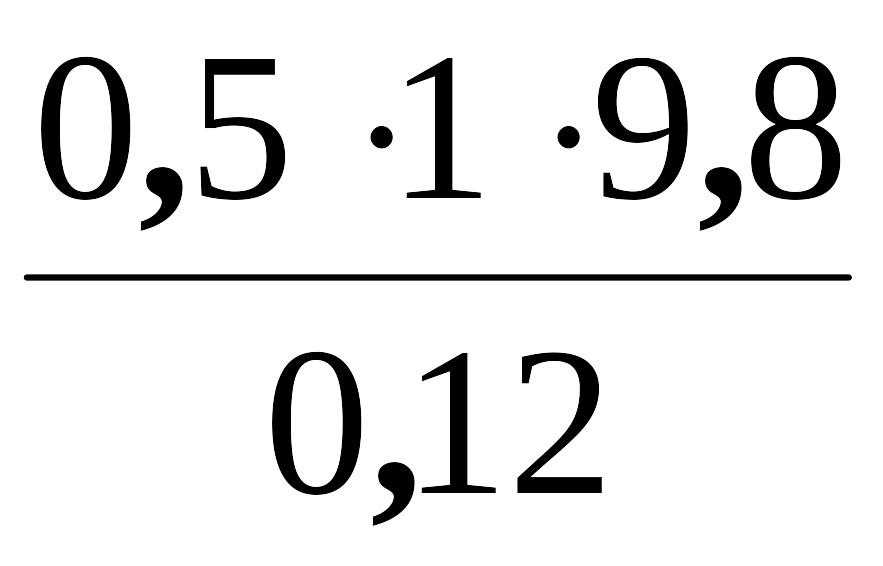= 4,1 Н.

Задача 14

Шар массой m = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.

Решение

Кинетическая энергия катящегося тела равна:

E_k = + . (12)

Момент инерции шара I = ,

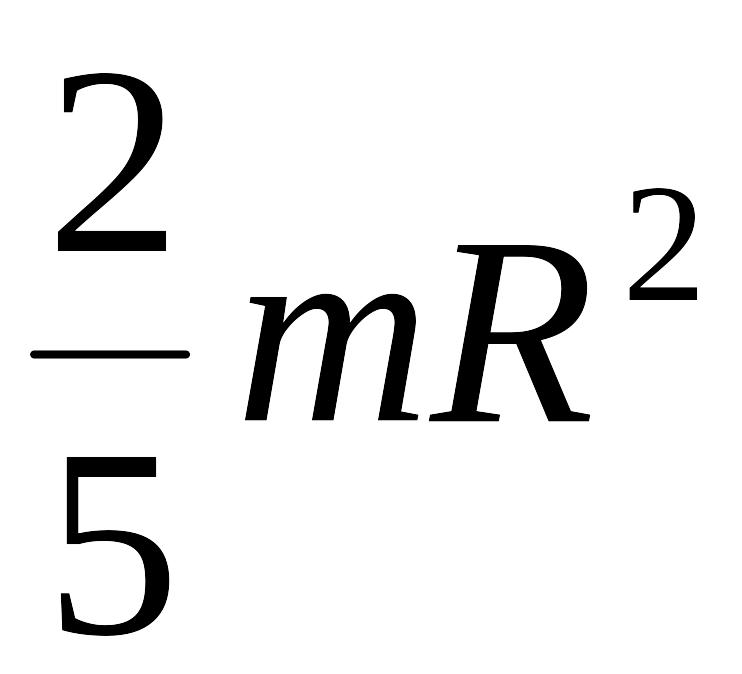угловая скорость вращения w = .

Подставляем эти величины в формулу (12):

E_k = + 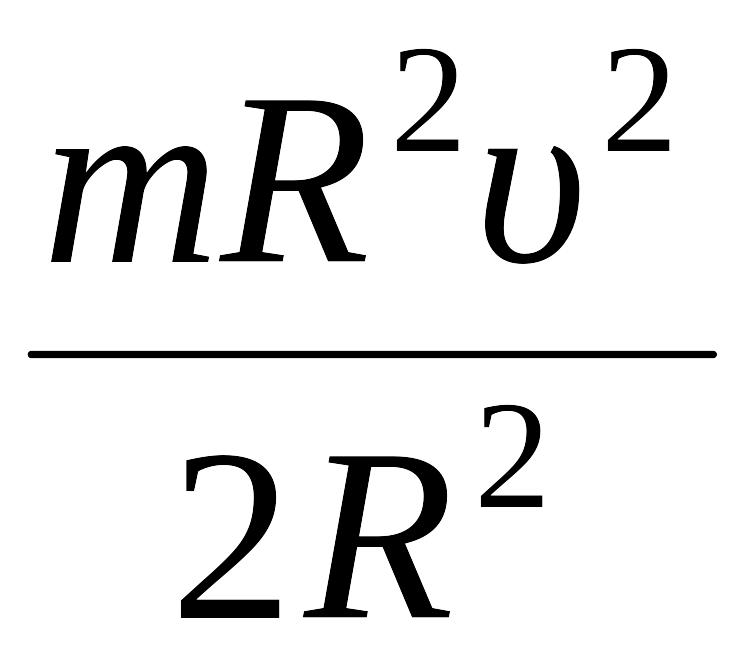= m υ ².

Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:

Q = E_k1 – E_k2 = m υ₁² - m υ₂² = m(υ₁² - υ₂²).

Подставив числовые значения, получим:

а = ∙1(100∙10^-4 – 64^.10^-4) = 10^-4 = 2,25∙10^-3 Дж = 2,52 МДж.

Задача 15

Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m₁ = 3 кг. Колеса считать тонкими обручами.

Решение

Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.

E_k = + .

Момент инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения w = .

Подставляем эти значения в выражение для кинетической энергии: E_k = + = .

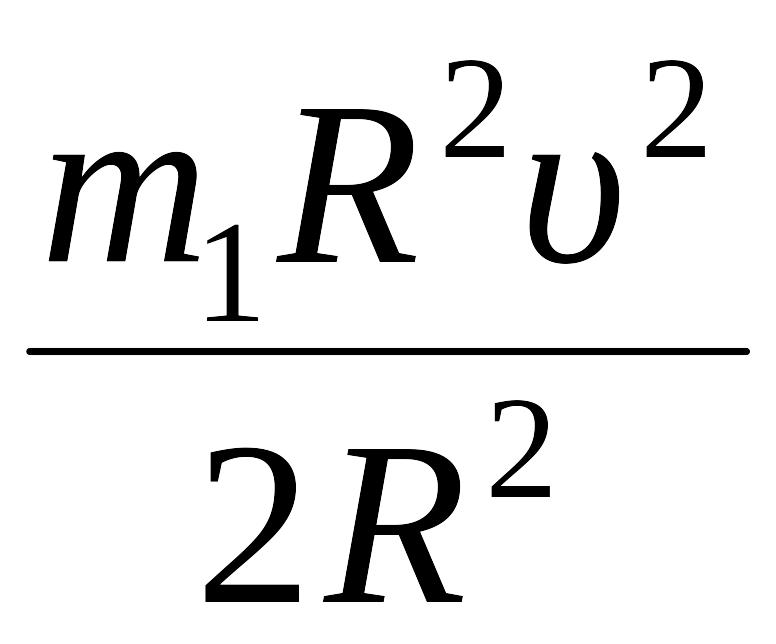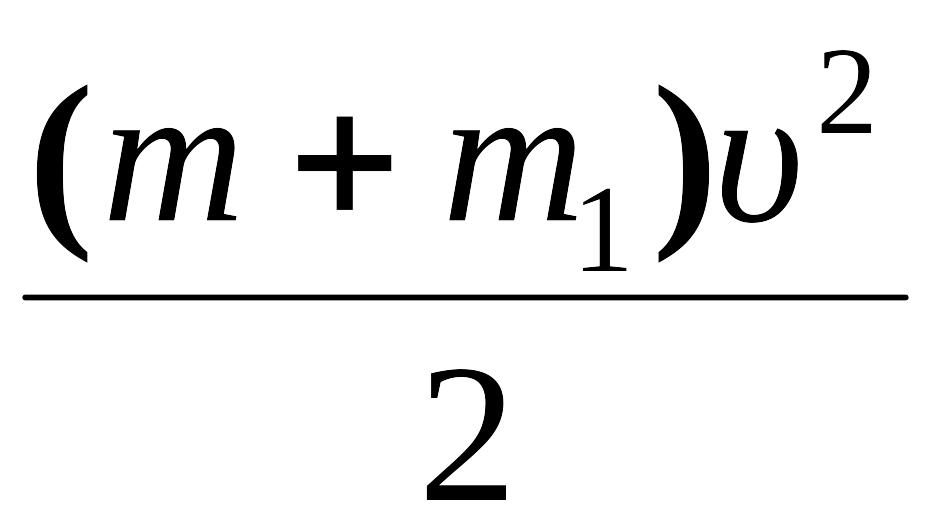Скорость надо перевести в м/с: υ = 2,5 м/с.

Подстановка числовых значений дает: E_k =253 Дж.