Задачи для самостоятельного решения

1. Пуля, летящая горизонтально, попадает в шар, подвешенный на очень легком жестком стержне и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти первоначальную скорость пули, если стержень с шаром отклонился от удара пули на угол 10.

2. Шар массой m₁ = 5 кг движется со скоростью v₁ = 1 м/с и сталкивается с покоящимся шаром массой m₂ = 2 кг. Определить скорости u₁ и u₂ шаров после удара. Шары считать однородными и абсолютно упругими, удар  прямым, центральным.

3. Тело массой 2 кг движется навстречу второму телу массой 1,5 кг и абсолютно неупруго соударяется с ним. Скорости тел непосред­ственно перед ударом были 1 м/с и 2 м/с. Какое время будут двигаться эти тела после удара, если коэффициент трения равен 0,05?

4. Пренебрегая трением, определить наименьшую высоту h, с которой должна скатываться тележка с человеком по желобу, переходящему в петлю радиуса R = 6 м, и не оторваться от него в верхней точке петли.

5. Спортсмен с высоты h = 12м падает на упругую сетку. Пренебрегая массой сетки, определить, во сколько раз наибольшая сила давления спортсмена на сетку больше его силы тяжести, если прогиб сетки под действием силы тяжести спортсмена х_о = 15 см.

6. Пуля массой m = 12 г, летящая с горизонтальной скоростью υ = 0,6 км/с, попадает в мешок с песком массой М = 10 кг, висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) долю кинетической энергии, израсходованной на пробивание песка.

7. Два шара массами m₁= 200 г и m₂ =400 г подвешены на нитях длиной l = 67,5 см. Первоначально шары соприкасаются между собой, затем первый шар отклонили от положения равновесия на угол α = 60° и отпустили. Считая удар упругим, определить на какую высоту h поднимется второй шар после удара.

8. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара m₁ = 0,2 кг, масса второго шара m₂ = 100 г. Первый шар отклоняют так, что его центр поднимается на высоту h = 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если удар неупругий?

9. Шар массой m₁ = 1 кг движется со скоростью v₁ = 4 м/с и сталкивается с шаром массой m₂ = 2 кг, движущимся навстречу ему со скоростью v₂ = 3 м/с. Каковы скорости шаров после удара? Удар считать абсолютно упругим, прямым, центральным.

10. Шар массой m₁ = 4 кг сталкивается с покоящимся шаром большей массы и при этом теряет 30% кинетической энергии. Определить массу m₂ большего шара. Удар считать абсолютно упругим, прямым, центральным.

4. Динамика вращательного движения твердого тела Основные формулы

Мерой инертности твердого тела при вращательном движении является момент инерции:

I = Σ m_i∙ r_i²,

где m_i – элементарная масса i – го кусочка тела, r_i – расстояние этого кусочка от оси вращения.

Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:

Полый цилиндр I = m ( R₁² + R₂²).

Тонкий обруч I = mR².

Сплошной цилиндр I = mR².

Шар I = mR².

Тонкий стержень I = ml².

Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:

I = I₀ + ma²,

где I – момент инерции тела относительно данной оси, I₀ – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, m – масса тела, а – расстояние между осями.

Основное уравнение динамики вращательного движения твердого тела:

I e = M,

где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.

Момент силы F равен: M = F l,

где l – расстояние от линии, вдоль которой действует сила, до оси вращения.

Момент импульса твердого тела относительно неподвижной оси:

L = I ω,

где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.

Момент импульса материальной точки относительно неподвижной оси:

L = m υ r,

где m – масса частицы, υ – ее скорость, r – расстояние от линии, вдоль которой движется частица, до данной оси.

В замкнутой системе частиц полный момент импульса не меняется:

ΣL_i = const.

Кинетическая энергия вращающегося тела:

E_k = ,

где I – момент инерции тела, ω – его угловая скорость.

Кинетическая энергия катящегося тела:

E_k = + ,

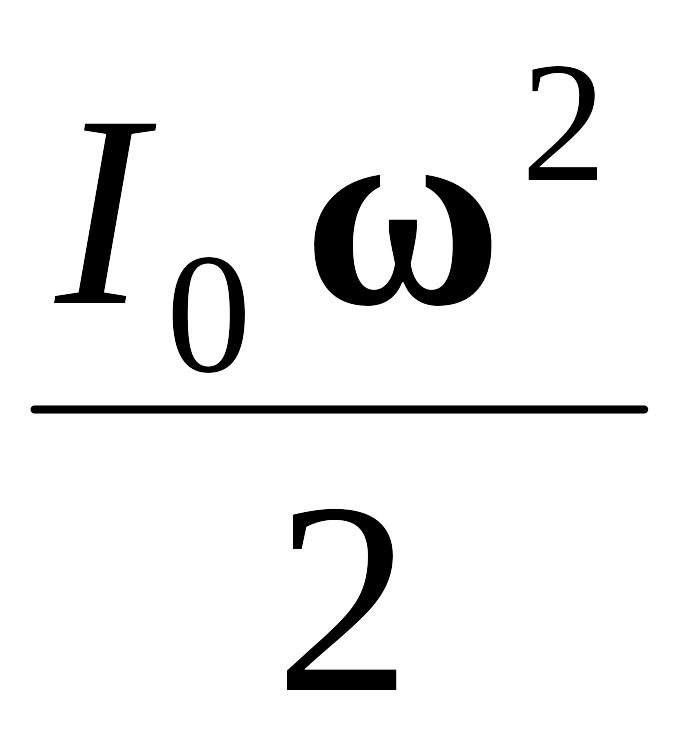где m – масса тела, υ₀ – скорость поступательного движения центра масс, I₀ – момент инерции тела относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.