3. Законы сохранения импульса и энергии Основные формулы

Работой силы F на перемещении ds называется произведение проекции силы на направление перемещения на это перемещение:

dA = F_s ds = Fds cosα,

где α – угол между направлениями силы и перемещения.

Работа переменной силы вычисляется как: A = .

Мощностью называют работу, произведенную за единицу времени: N = .

Мгновенная мощность равна скалярному произведению силы, действующей на тело, на его скорость: N = .

Кинетическая энергия тела при поступательном движении: ,

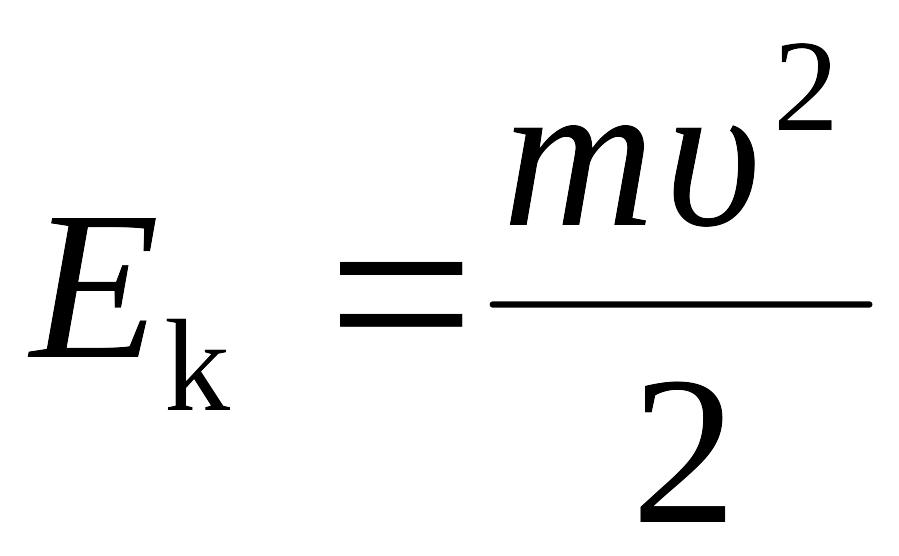где m – масса тела, υ – его скорость.

Потенциальная энергия тела

– в однородном поле тяжести: E_п = mgh

(m – масса тела, g – ускорение свободного падения, h – высота тела над точкой, в которой потенциальная энергия принимается равной нулю);

– в поле упругих сил: E_п =

(k – коэффициент жесткости упругого тела, x – смещение от положения равновесия).

В замкнутой системе частиц полный импульс системы не меняется в процессе ее движения:

Σ = const.

В замкнутой консервативной системе частиц сохраняется полная механическая энергия:

E = E_k + E_п = const.

Работа сил сопротивления равна убыли полной энергии системы частиц или тела:

A_conp = E₁ – E₂.

Примеры решения задач

Задача 6

Вагон массой 20 т, двигавшийся равномерно, под действием силы трения в 6 кН через некоторое время остановился. Начальная скорость вагона равна 54 км/ч. Найти: 1) работу сил трения; 2) расстояние, которое вагон пройдёт до остановки.

Решение

Работа равна приращению кинетической энергии тела:

A_тр = 0 – = – ,

Знак «–» означает, что работа сил трения отрицательна, так как силы трения направлены против движения.

С другой стороны, работу силы трения можно рассчитать через произведение силы на путь:

A_тр = F_тр^. S,

отсюда S = =

Подставив числовые значения:

m = 2^.10⁴ кг, F_тр = 6^.10³ Н, υ = 15 м/с,

получим:

A_тр = 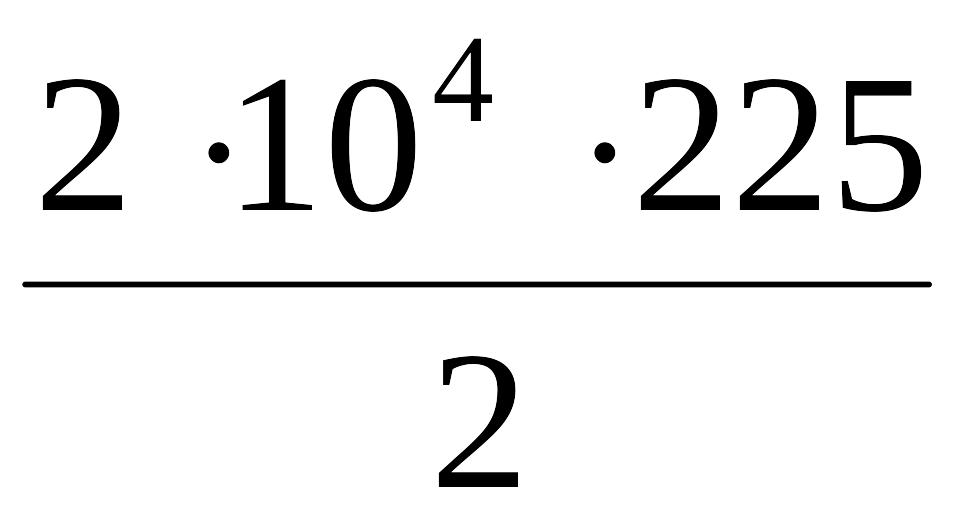= 2,25^.10⁶ Дж = 2,25 МДж,

S = 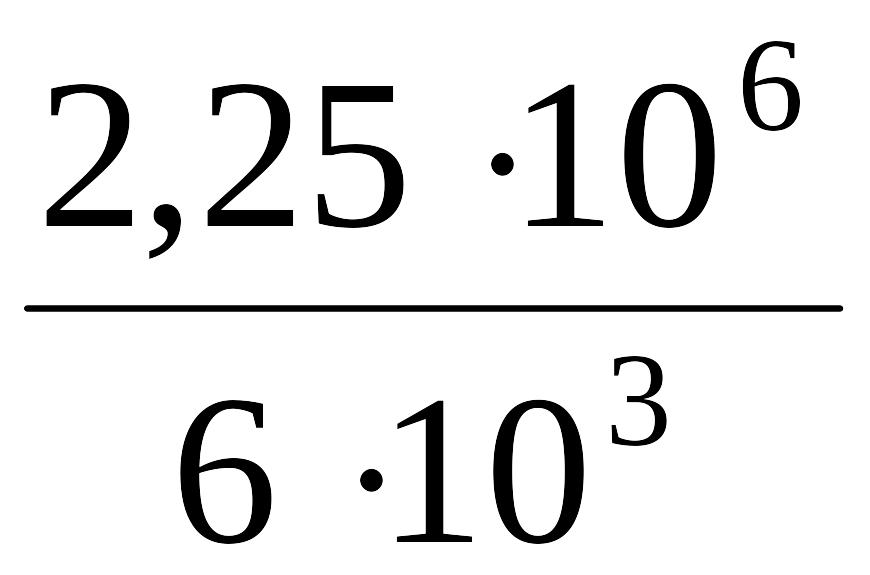= 358 м.

Задача 7

Камень бросили под углом α = 60^о к горизонту со скоростью υ₀=15 м/с. Найти кинетическую, потенциальную и полную энергию камня: 1) спустя одну секунду после начала движения; 2) в высшей точке траектории. Масса камня m = 0,2 кг. Сопротивлением воздуха пренебречь.

Решение

Выберем ось х – по горизонтали, а ось у – по вертикали.

Проекции скорости:

υ_x = υ₀ cos a, (6)

υ_о υ_y = υ₀ sin a – gt (7)

a x В момент времени t модуль скорости определится из соотношения:

υ² = υ₀² cos² a+ (υ₀ sin a – gt)² = υ₀² – 2 υ₀ gt sin a + g²t².

Высота камня над поверхностью земли в момент времени t определяется из соотношения:

h = υ₀ sin a - . (8)

Находим кинетическую, потенциальную и полную энергию в момент времени t:

E_k = = ( υ₀² – 2 υ₀ gt sin a + g²t²),

E_п = mgh = ( 2 υ₀ gt sin a – g²t²),

E = E_k + E_п= .

В высшей точке траектории υ_y = 0. Этой точки камень достигает за время = 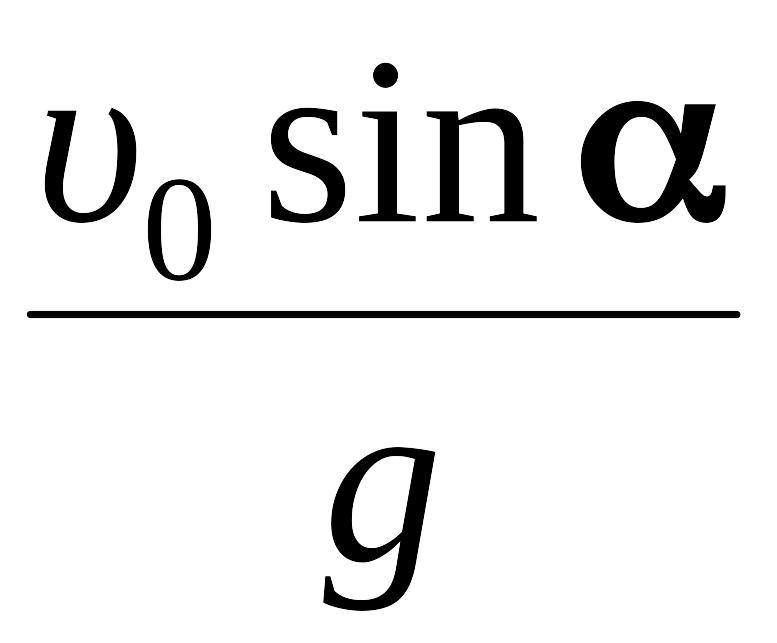(из (7)), и максимальная высота подъёма h_max= (из (8)).

E_k = = ,

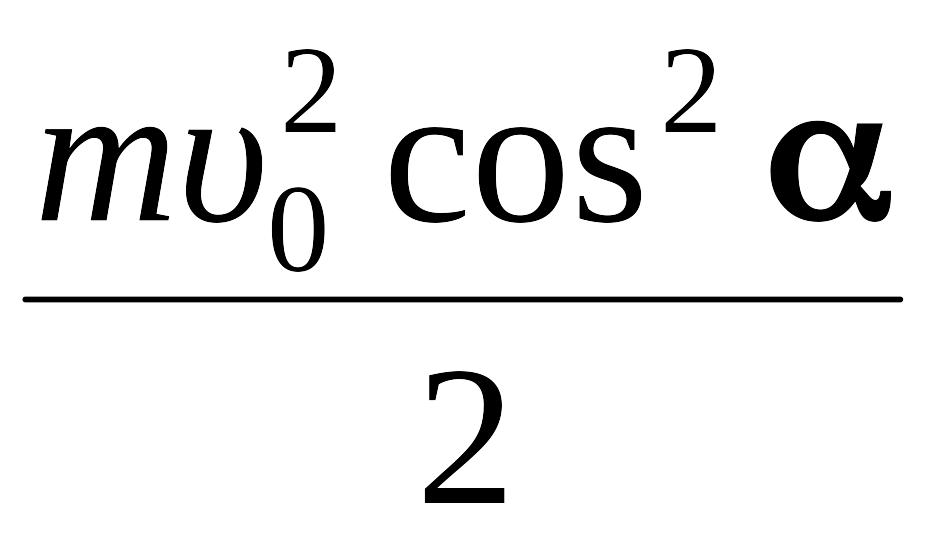E_п = mgh_max = ,

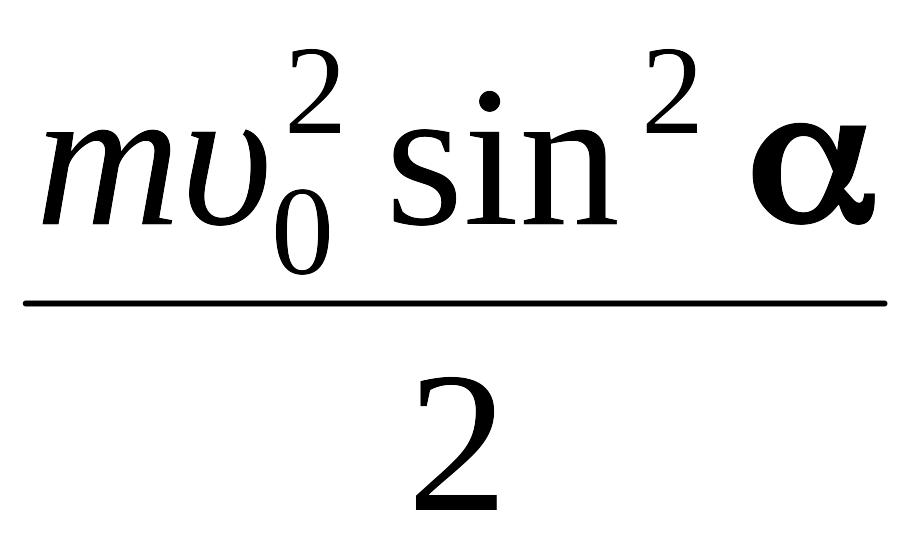E = E_k + E_п = .

Подставляем числовые значения. В момент времени t = 1 c.

E_k = 17,4 Дж, E_п = 5,1 Дж, E = 22,5 Дж.

В высшей точке траектории:

E_k = 16,9 Дж, E_п = 5,6 Дж, E = 22,5 Дж.

Задача 8

На рельсах стоит платформа массой m₁ = 10 т, на платформе закреплено орудие массой m₂ = 5 т, из которого проводится выстрел вдоль рельсов. Масса снаряда m₃ = 100 кг, его начальная скорость относительно орудия υ₀ = 500 м/с. Определить скорость υ_x платформы в первый момент времени, если: 1) платформа стояла неподвижно, 2) платформа двигалась со скоростью υ₁ = 18км/ч, и выстрел был произведён в направлении её движения, 3) платформа двигалась со скоростью υ₁ = 18 км/ч, и выстрел был произведён в направлении, противоположном её движению.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы до какого-либо события (в данном случае выстрела) должен быть равен её импульсу после события. За положительное выбираем направление скорости снаряда. До выстрела вся система имела импульс (m₁+m₂+m₃)υ₁, после выстрела платформа с орудием движутся со скоростью υ_x, их импульс (m₁+m₂)υ_x, а снаряд относительно земли движется со скоростью υ₀+ υ₁, его импульс m₃(υ₀+υ₁). Закон сохранения импульса записывается так:

(m₁ + m₂ + m₃) υ₁ = (m₁ + m₂) υ_x + m₃(υ₀+ υ₁),

отсюда υ_x = 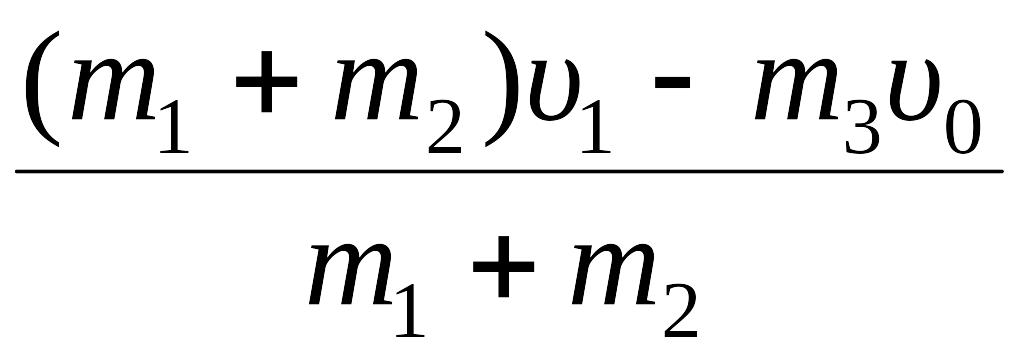= υ₁ – υ₀.

Подставляем значения масс, υ₁ и υ₀:

1) υ₁ = 0

υ_x = – 3,33 м/с.

Знак минус означает, что платформа с орудием движется противоположно направлению движения снаряда;

2) υ₁ = 18 км/ч = 5 м/с,

υ_x = 5 – 3,33 = 1,67 м/с.

Платформа с орудием продолжает двигаться в направлении выстрела, но с меньшей скоростью;

3) υ₁ = – 18 км/ч = – 5 м/с

υ_x = – 5 – 3,33 = – 8,33 м/с.

Скорость платформы, двигавшейся в направлении, противоположном направлению выстрела, увеличивается.

Задача 9

Пуля, летящая горизонтально, попадает в шар, подвешенный на лёгком жёстком стержне, и застревает в нём. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара на угол 10^о.

Решение.

Если пуля застревает в шаре, то удар

абсолютно неупругий, и выполняется только закон сохранения импульса. До удара пуля имела импульс mυ, шар импульса не имел. Непосредственно после удара пуля с шаром имеют общую скорость υ₁, их импульс (M + m) υ₁.

Закон сохранения импульса:

m υ = (M + m) υ₁,

отсюда υ₁ = 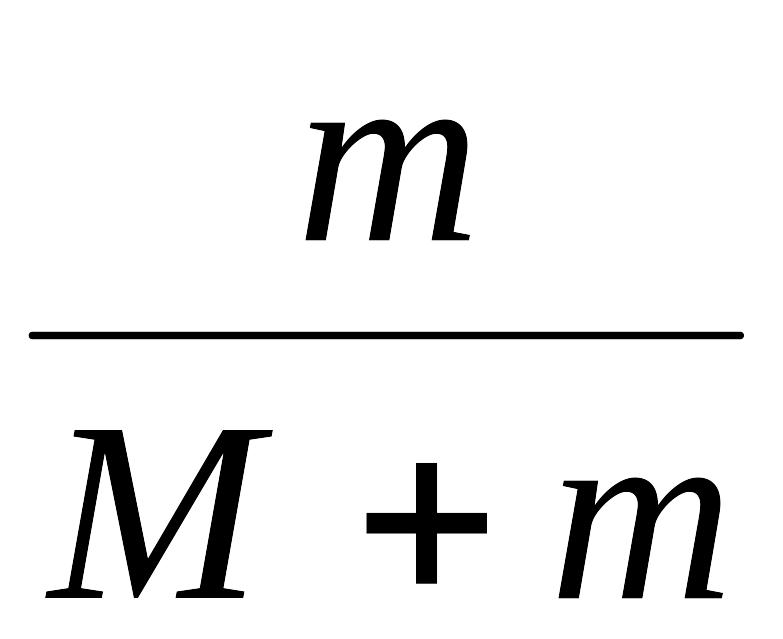υ.

Шар вместе с пулей в момент удара приобрёл кинетическую энергию:

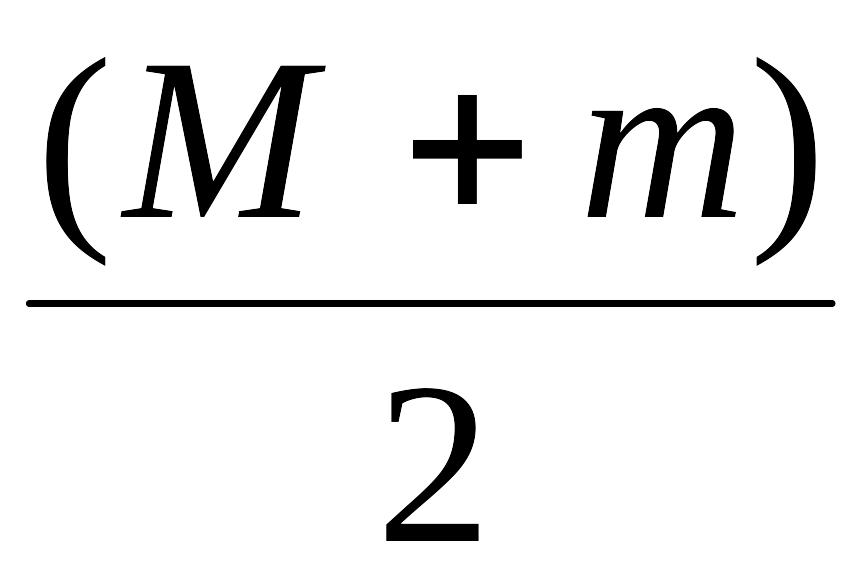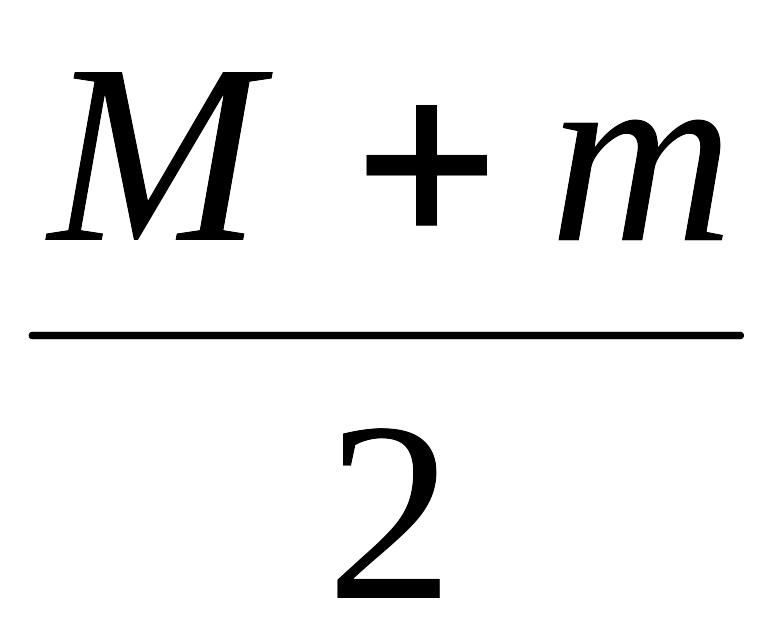
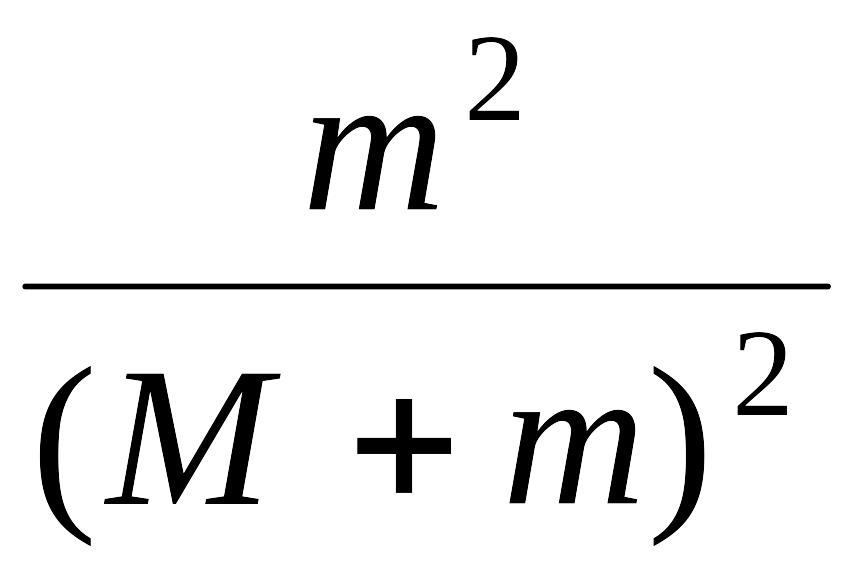E_k = υ₁² = υ² = .

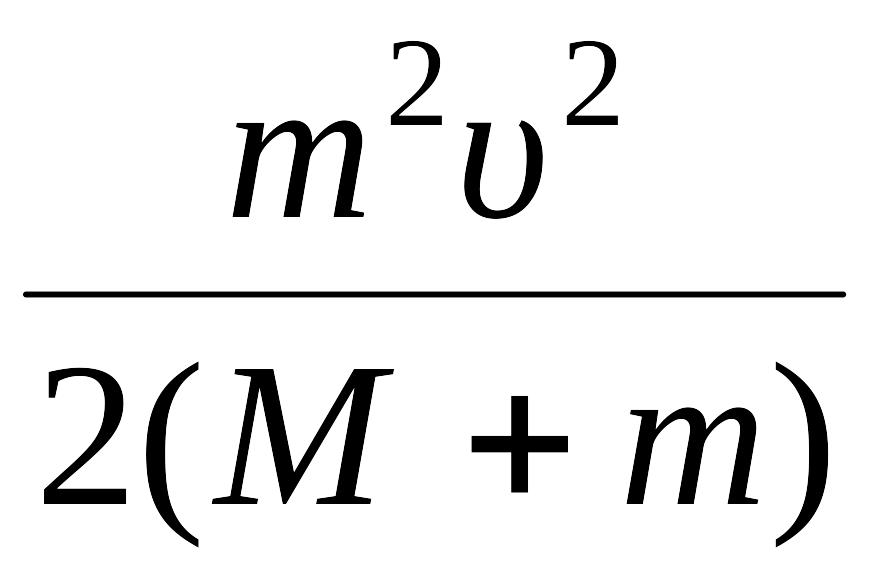За счёт этой энергии шар поднялся на высоту h, при этом его кинетическая энергия переходит в потенциальную:

E_k = E_п Þ = (M + m) gh. (9)

Высоту h можно выразить через расстояние от точки подвеса до центра шара и угол отклонения от вертикали

h = L – L cos a = L(1 – cos a).

Подставив последнее выражение в соотношение (9), получим:

a L = gL(1 – cos a),

h и определим скорость пули:

υ = .

Подставив числовые значения, получим:

υ = 1001 » 543 м/с.

Задача 10

К амень, привязанный к верёвке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями верёвки равны 9,8 Н.

Решение

В верхней точке траектории и сила тяжести, и сила натяжения верёвки направлены вниз.

L Уравнение движения в верхней точке имеет вид:

ma_n = m = mg + T₁.

В нижней точке траектории сила тяжести направлена вниз, а сила натяжения верёвки и нормальное ускорение вверх. Уравнение движения в нижней точке:

ma_n = m = T₂ – mg.

По условию камень вращается с постоянной скоростью, поэтому левые части обоих уравнений одинаковы. Значит, можно приравнять правые части:

mg + T₁ = T₂ – mg,

отсюда T₂ – T₁ = 2mg,

m = .

Подставляем числа: m = 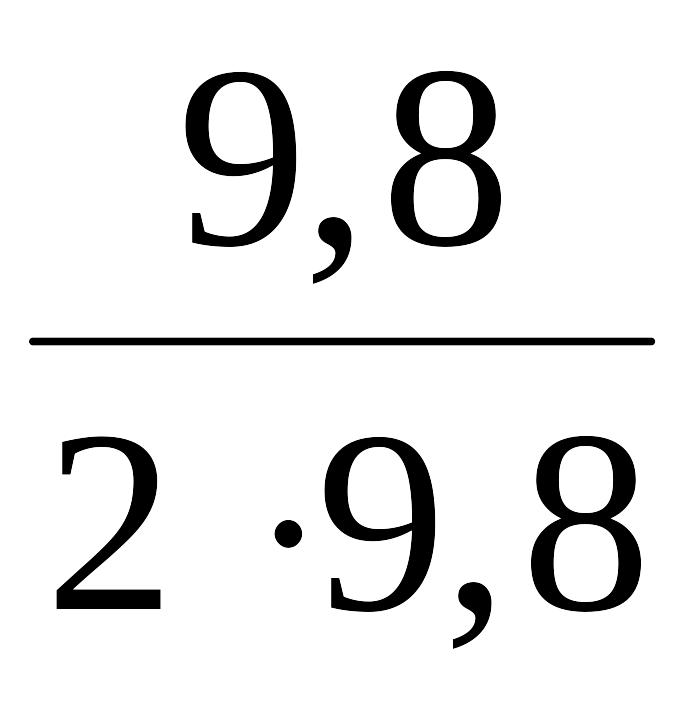= 0,5 кг.

Задача 11

Шоссе имеет вираж с уклоном в 10° при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?

Решение

Сила, действующая на автомобиль, складывается

из силы тяжести и силы нормального давления . Сумма этих сил обусловливает нормальное ускорение автомобиля при повороте.

Из треугольника сил видно, что: = tg a.

Рассчитаем a_n, сократив массу

= tg a,

отсюда υ = =41,5 м/с.