Решение типовых задач
Задача 24. Кислород массой 1 кг совершает цикл Карно. При изотермическом расширении газа его объём увеличивается в 2 раза, а при последующем адиабатическом расширении совершается работа 3000 Дж. Определить работу, совершенную за цикл.
Дано: V2 = 2V1 A2-3 = 3000 Дж i = 5 |
Решение: Идеальный цикл Карно состоит из двух изотерм и двух адиабат (рис. 3). |
А - ? |
На рисунке 3 участок 1-2 соответствует изотермическому расширению газа (Т1 = Т2), участок 2-3 – адиабатическому расширению газа, участок 3-4 – изотермическому сжатию (Т3 = Т4) и участок 4-1 – адиабатическому сжатию.
П
ри
изотермическом расширении внутренняя
энергия идеального газа остается
постоянной, следовательно, все подводимое
тепло Q1
идет на работу по расширению газа на
участке 1-2,
т.е.
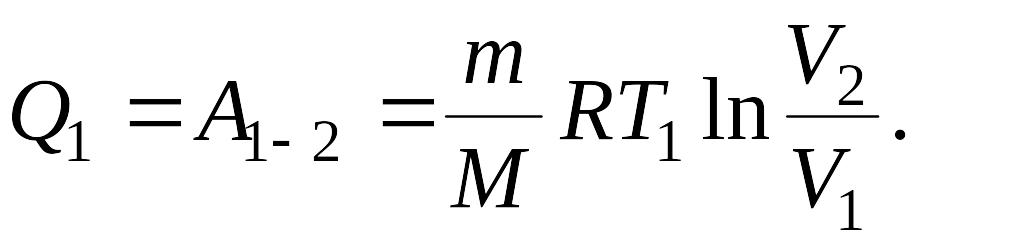(1)
При изотермическом сжатии на участке 3-4 Q2 тепло отдается холодильнику (Q2), и это количество теплоты определяется работой, затраченной на сжатие газа:
(2)
Состояния 2 и 3 лежат на одной адиабате, поэтому можно записать:
(3)
Для состояний 4 и 1, которые отвечают одной адиабате, имеем:
(4)
Поделив выражение (3) на (4), получим:
, (5)
так как Т1 = Т2 и Т3 = Т4.
Работа при адиабатическом расширении на участке 2-3 равна:
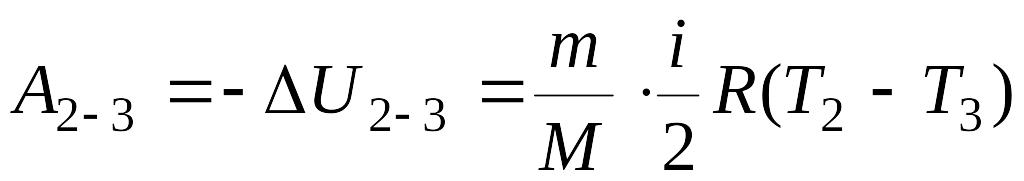(6)
Работа при адиабатическом сжатии на участке 4-1 равна:
.
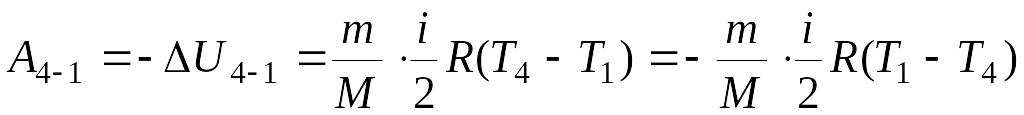Так как Т1 = Т2, а Т3 = Т4, то А2 - 3 = -А4 - 1, т.е. полная работа по адиабатическому сжатию и расширению равна нулю.
Следовательно, работа цикла: А = А1-2 – А3-4.
Из уравнений
(1), (2) и (5) получим:
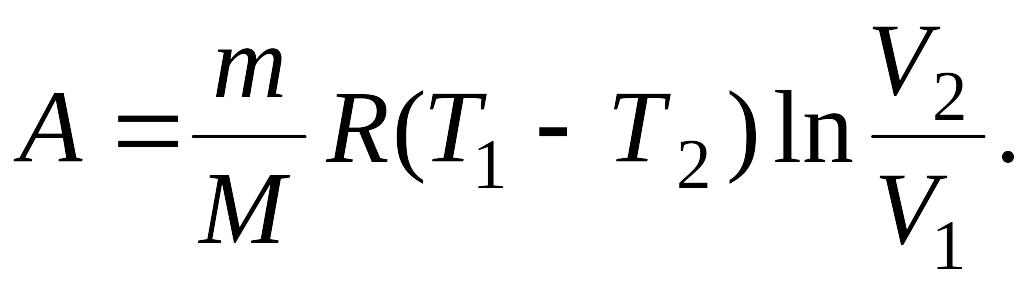(7)
Из
уравнения (6) выразим разность температур
Т2
– Т3,
равную Т1
– Т3,
и подставим в уравнение (7):
.
Произведем вычисления:
.
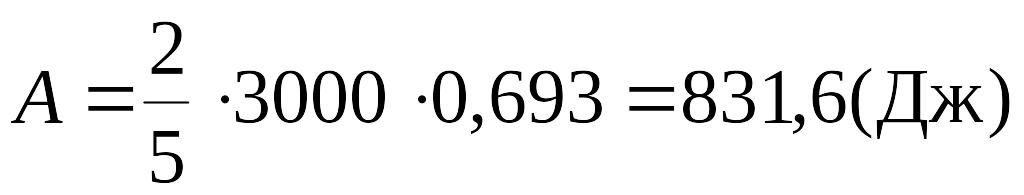Ответ: 831,6 Дж.
Задачи для самостоятельного решения
8.1. Идеальный газ совершает цикл Карно. Температура нагревателя Т1 = 500 К, холодильника Т2 = 300 К. Работа изотермического расширения газа составляет 2 кДж. Определить: 1) термический к.п.д. цикла; 2) количество теплоты, отданное газом при изотермическом сжатии холодильнику.
8.2. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, к.п.д. которого = 0,4, если работа А1 изотермического расширения равна 8 Дж.
8.3. Газ, совершающий цикл Карно, отдал холодильнику 67% теплоты, полученной от нагревателя. Определить температуру Т2 холодильника, если температура нагревателя Т1 = 430 К.
8.4. Во сколько раз увеличится коэффициент полезного действия цикла Карно при повышении температуры нагревателя от Т1 = 380 К до Т1 = 560 К? Температура холодильника Т2 = 280 К.
8.5. Газ, совершающий цикл Карно, получает количество теплоты Q1 = 84 кДж. Какую работу А совершает газ, если температура Т1 нагревателя в три раза выше температуры Т2 холодильника?
8.6. Тепловая машина работает по циклу Карно. Температура нагревателя Т1 = 500 К. Определить к.п.д. цикла и температуру Т2 холодильника, если за счет количества теплоты Q1 = 1 кДж, полученной от нагревателя, машина совершает работу А = 350 Дж.
8.7. Газ, совершающий цикл Карно, отдал холодильнику 76% теплоты, полученной от нагревателя. Определить температуру холодильника Т2, если температура нагревателя Т1 = 400 К.
8.8. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, к.п.д. которого = 0,4, если работа изотермического расширения А1 = 18 Дж.
8.9. Идеальная тепловая машина работает по циклу Карно. Температура нагревателя Т1 = 500 К, температура холодильника Т2 = 250 К. Определить к.п.д. цикла, а также работу А1, совершенную рабочим веществом при изотермическом расширении, если при изотермическом сжатии совершена работа А2 = 70 Дж.
8.10. Идеальная холодильная машина работает по обратному циклу Карно и потребляет мощность 1 кВт. При этом она забирает теплоту от тела с температурой -37 0С и отдает телу с температурой 67 0С. Определить к.п.д. цикла и количество теплоты, отнятое у холодного тела за 1 с.