
- •Примеры решения типовых задач
- •Задачи для самостоятельного решения
- •2. Динамика материальной точки. Законы Ньютона Основные уравнения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Законы сохранения импульса и энергии Основные формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4. Динамика вращательного движения твердого тела Основные формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5. Закон сохранения момента импульса Основные формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Основы мкт идеального газа. Уравнение состояния. Изопроцессы. Закон Дальтона Основные формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Первое начало термодинамики. Адиабатический процесс Основные формулы
- •Решение типовых задач
- •Задачи для самостоятельного решения
- •8. Циклические процессы. Кпд цикла. Цикл Карно Основные формулы
- •Решение типовых задач
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
В закрытом сосуде вместимостью 20 л находятся водород массой 6 г и гелий массой 12 г. Определить давление и молярную массу газовой смеси в сосуде, если температура смеси Т = 300 К.
Определить молярную массу и плотность смеси газов водорода массой m1 = 8 г и кислорода массой m2 = 64 г при температуре Т = 290 К и при давлении 0,1 МПа. Газы считать идеальными.
Баллон вместимостью V = 20 л содержит смесь водорода и азота при температуре 290 К и давлении 1 МПа. Определить массы водорода и азота, если масса смеси равна 150 г.
Два сосуда одинакового объема содержат кислород. В одном сосуде давление р1 = 3 МПа и температура Т1 = 700 К, в другом р2 = 1,5 МПа, Т2 = 200 К. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры Т = 180 К. Определить установившееся в сосудах давление р.
Баллон содержит 80 г кислорода и 320 г аргона. При температуре Т = 300 К давление смеси равняется 1 МПа. Считая газы идеальными, определить объем баллона и молярную массу смеси газов.
В баллоне емкостью V = 15 л находится смесь, содержащая 10 г водорода, 54 г водяного пара и 60 г окиси углерода. Определить молярную массу и давление смеси при температуре t = 27С.
Какое количество кислорода выпустили из баллона объемом V = 10 л, если при этом показания манометра на баллоне изменились от Р1 = 16105 Па до Р2 = 7105 Па, а температура понизилась от t1 = 27С до t2 = 7С?
Азот массой m = 5 г, находящийся в закрытом сосуде объемом V = 4 л при температуре t1 = 20С, нагревается до температуры t2 = 40С. Найти давление газа до и после нагревания.
В баллоне объемом V = 22,4 л находится водород при нормальных условиях. После того, как в баллон ввели некоторое количество гелия, давление в баллоне возросло до р = 0,25 МПа. Определить массу гелия, введенного в баллон, если температура газа при этом не изменилась.
В двух сосудах одинакового объема содержится кислород. В одном сосуде газ находится при давлении p1 = 2 МПа и температуре Т1 = 800 К, а в другом при давлении p2 = 2,5 МПа и температуре Т2 = 200 К. Сосуды соединили между собой трубкой и охладили находящийся в них кислород до температуры Т = 200 К. Определить установившееся в сосудах давление.
Первое начало термодинамики. Адиабатический процесс Основные формулы
Первое начало термодинамики
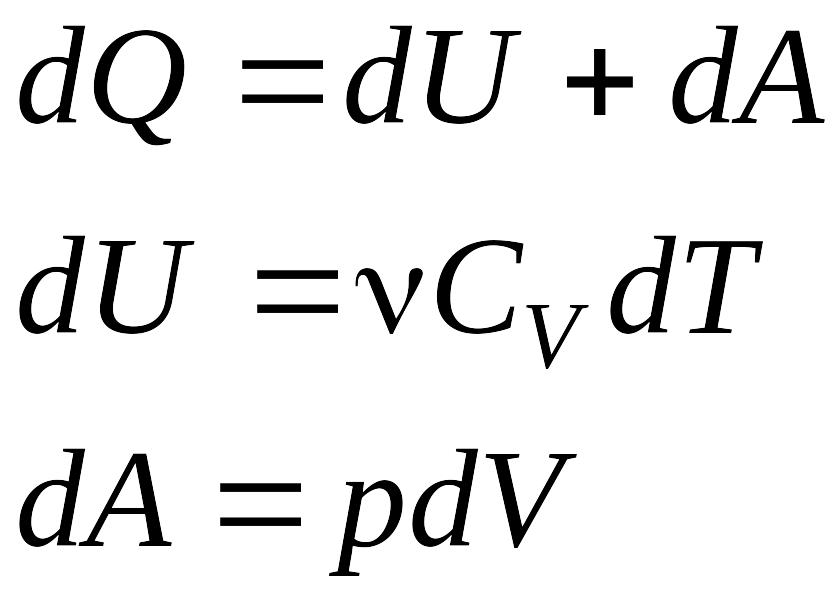
Работа расширения газа при процессе:
Изобарном ![]() ,
,
Изотермическом 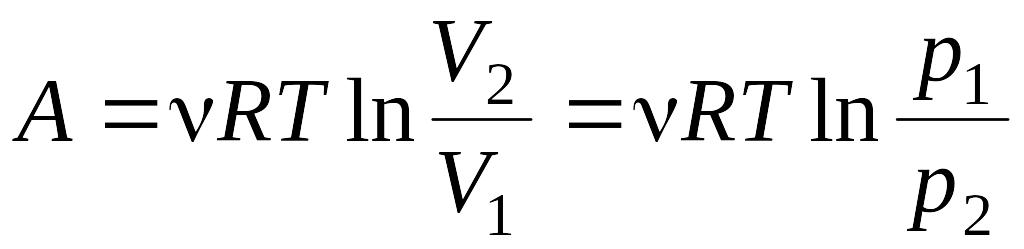 ,
,
Адиабатном
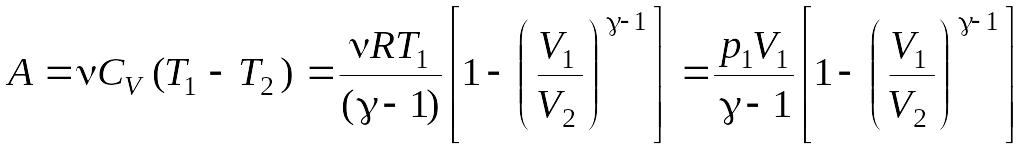 ,
где
,
где
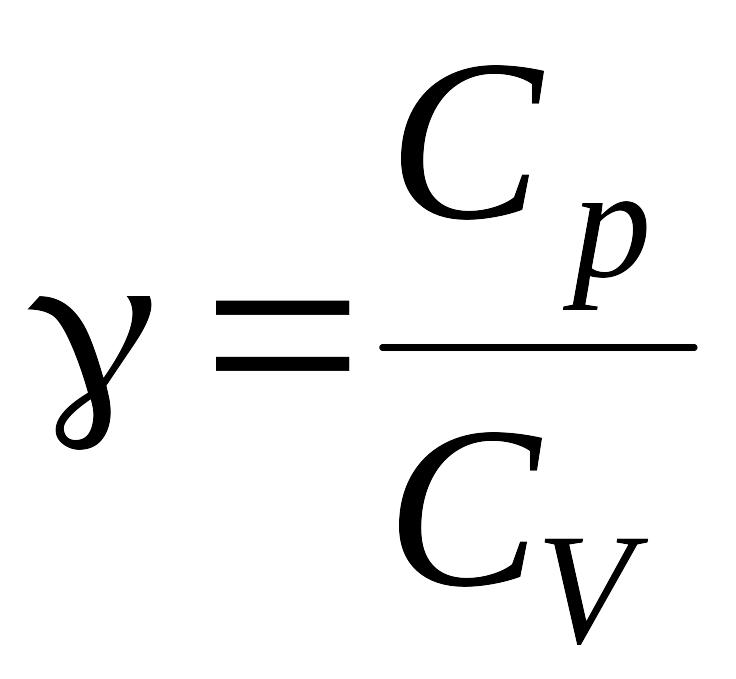 .
.
Уравнение Пуассона (уравнение адиабатного процесса)
![]() ,
,
![]() ,
,
![]() .
.
Решение типовых задач
Задача 19. При адиабатическом сжатии давление воздуха было увеличено от Р1 = 100 кПа до Р2 = 1 МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление Р3 газа в конце процесса.
Р1 =100 кПа=1·105 Па Р2 = 1 МПа =1·106 Па V2 = const = 1,4 Р3 – ?
|
Решение: На PV диаграмме представлен график, соответствующий процессу, указанному в условии задачи.
|
Процесс адиабатического сжатия 1-2 совершается без теплообмена и согласно уравнению Пуассона:
![]()
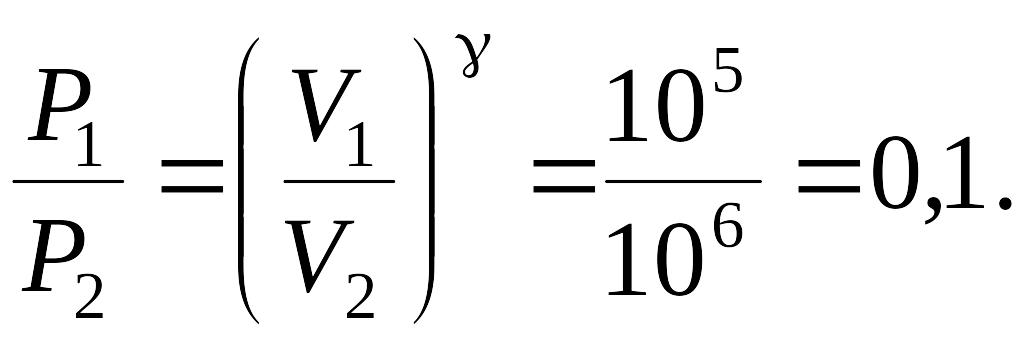 (1)
(1)
Макроскопические параметры P, V, T воздуха в состоянии 1, 2, 3 связаны соотношением:
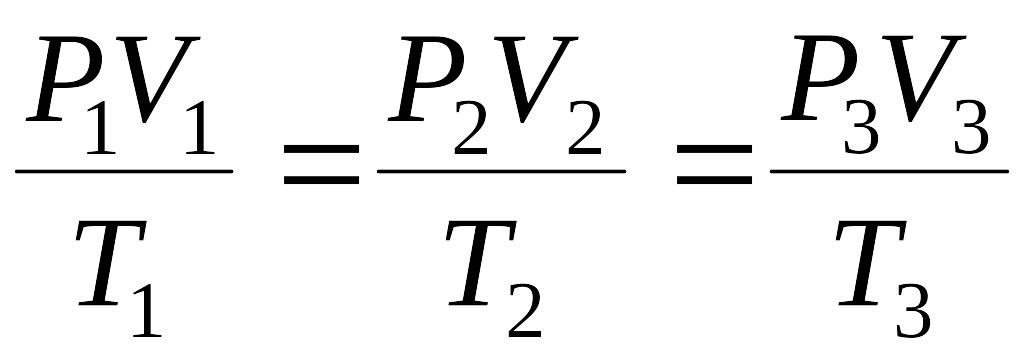 ,
,
откуда P1V1 = P3V3.
По условию задачи V2 = V3. Используя уравнение (1) можно записать
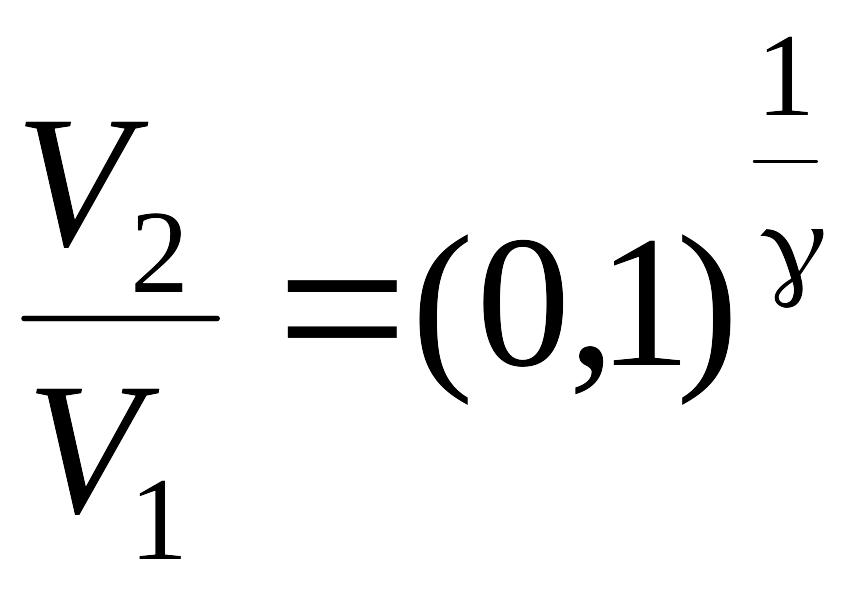 .
.
Тогда
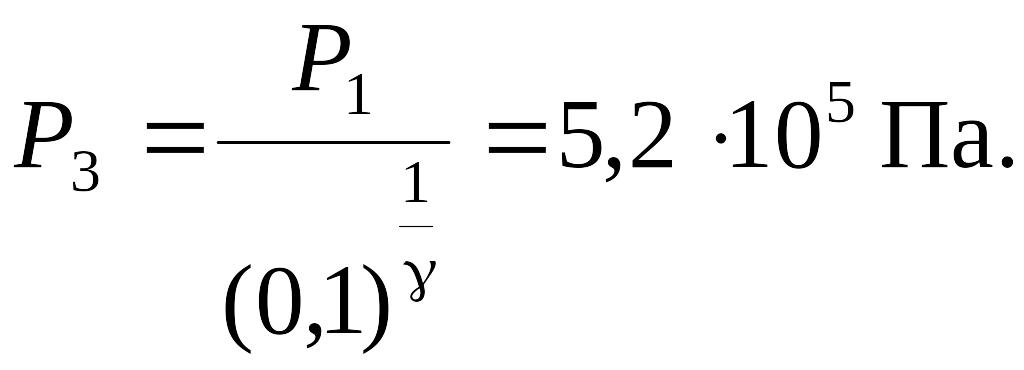
Ответ:
![]()
Задача 20. Определить скорость вылета поршня массой 4 кг из цилиндра при адиабатном расширении кислорода в 40 раз, если начальное давление воздуха 107 Па, а объем 0,3 л.
Дано: Т = 4 кг V2/V1 = 40 p1 = 10 7Па V1 = 0,3 л = 3·10-4 м3 |
Решение: Работа А, совершаемая адиабатически расширяющимся воздухом, в данном случае идет на увеличение кинетической энергии поршня, т. е |
υ - ? |
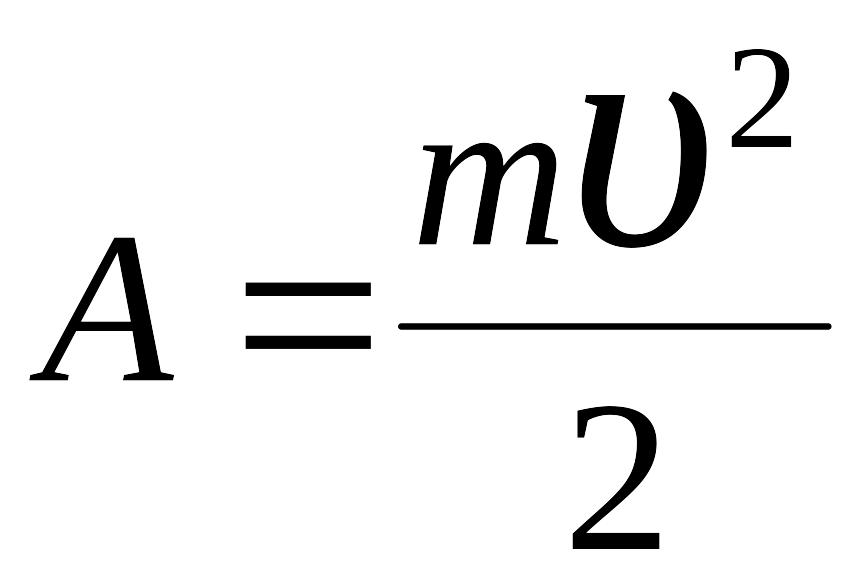 ,
,
где т и υ – масса и скорость поршня.
Для
подсчета работы адиабатически
расширяющегося газа воспользуемся
формулой:
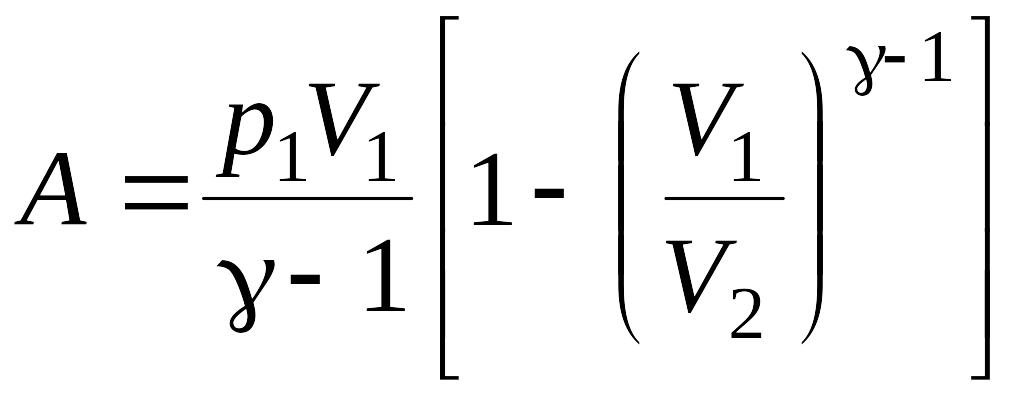 ,
где γ – отношение теплоемкостей газа
при постоянном давлении и постоянном
объеме (для кислорода γ =1,4).
,
где γ – отношение теплоемкостей газа
при постоянном давлении и постоянном
объеме (для кислорода γ =1,4).
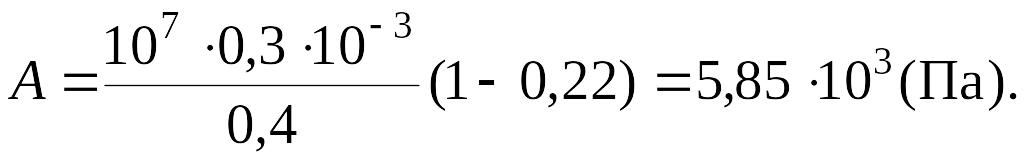 Так как
,
то
Так как
,
то
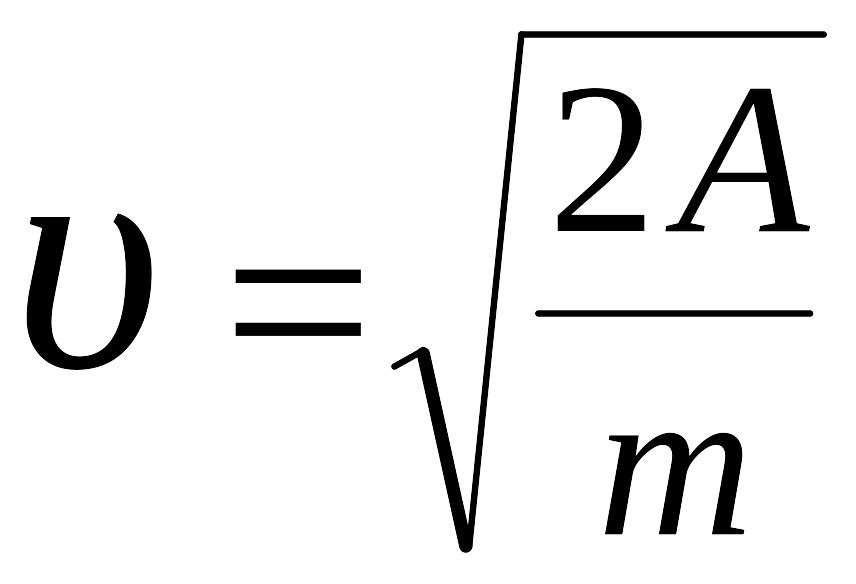 ,
,
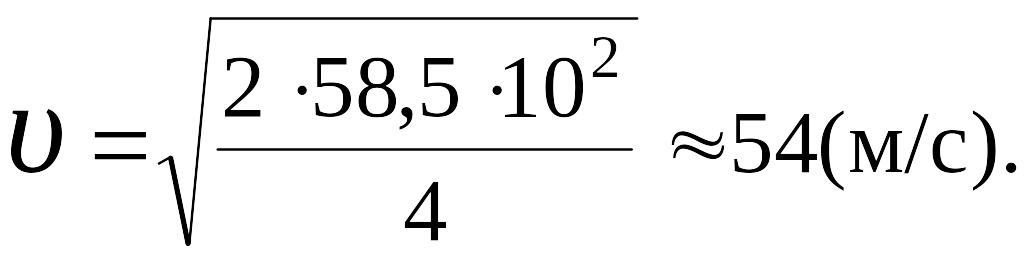
Ответ: 54 м/с.
Задача 21. Определить удельные теплоемкости ср, сv, для смеси 1 кг азота и 1 кг гелия.
Дано: m1= 1 кг М1= 28 кг/кмоль i1 = 5 m2 = 1 кг М2= 4 кг/кмоль газа. i2 = 3 |
Решение:
Удельной теплоемкостью какого – либо газа называется величина, равная количеству теплоты, которое нужно сообщить единице массы тела, чтобы повысить его температуру на 1 градус. При этом величина теплоемкости зависит от условий, при которых происходит нагревание. |
ср - ? сv - ? |
Если
нагревание происходит при постоянном
объеме, то:
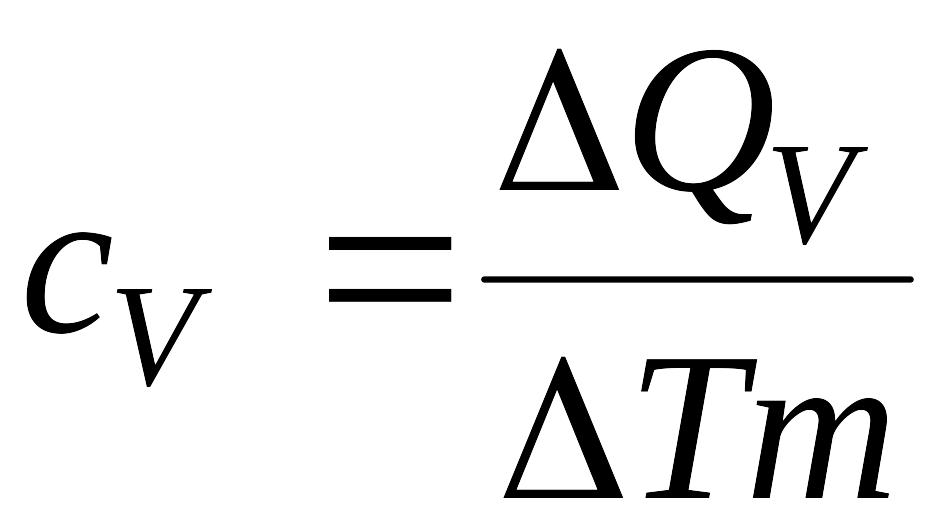 ,
где
,
где
![]() ,
т.е. все сообщаемое количество теплоты
идет на изменение внутренней энергии
системы. Изменение внутренней энергии
смеси газа определяется формулой:
,
т.е. все сообщаемое количество теплоты
идет на изменение внутренней энергии
системы. Изменение внутренней энергии
смеси газа определяется формулой: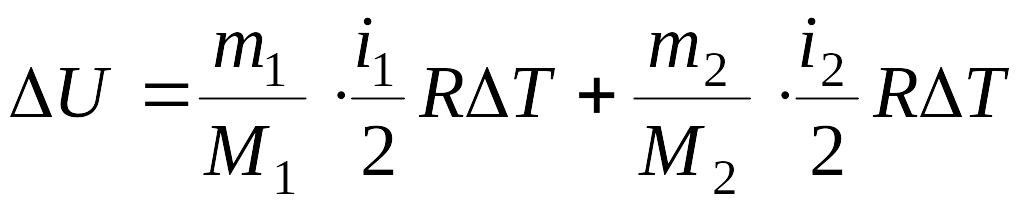 ,
где i1 и i2
– число степеней свободы первого и
второго газов.
,
где i1 и i2
– число степеней свободы первого и
второго газов.
Окончательно
получим:
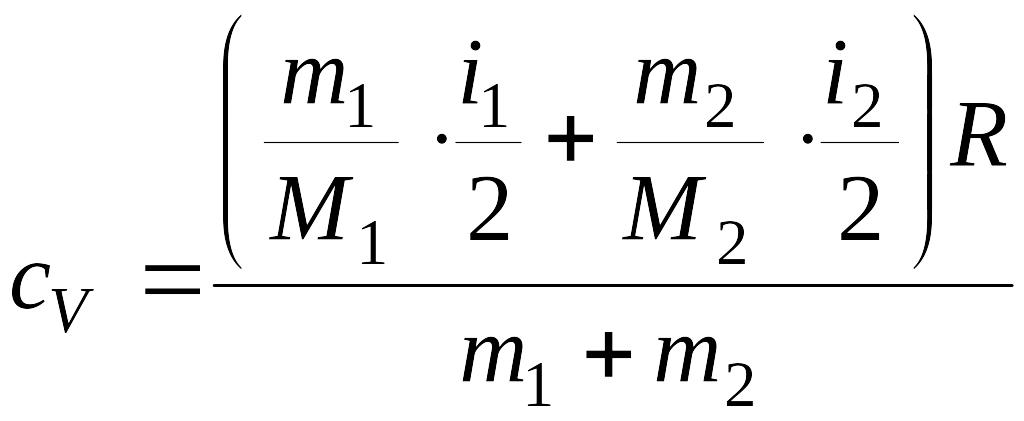 . (1)
. (1)
Если нагревание происходит при постоянном давлении, то
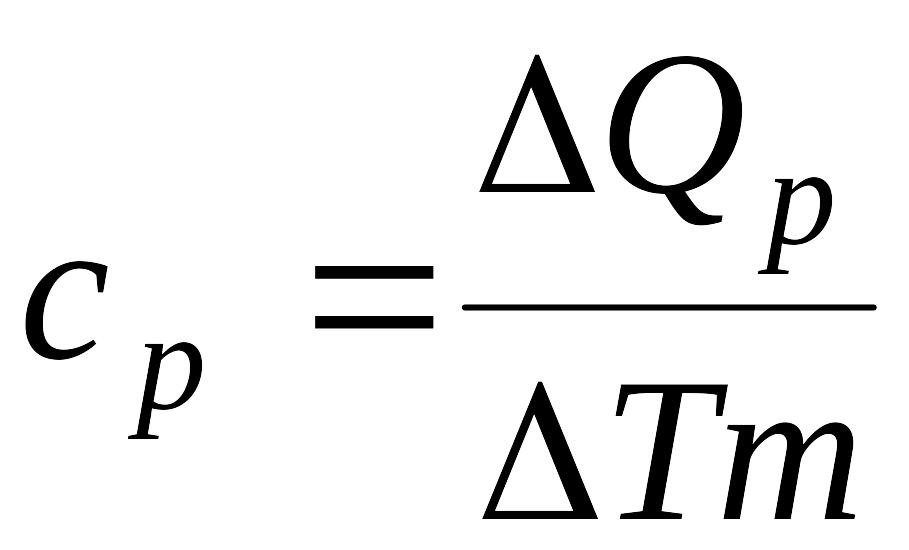 , (2)
, (2)
где
![]() ,
т.е. сообщаемое газу количество теплоты
идет не только на изменение внутренней
энергии, но и на работу по расширению
газа. Работа при изобарическом расширении
для каждого газа равна:
,
т.е. сообщаемое газу количество теплоты
идет не только на изменение внутренней
энергии, но и на работу по расширению
газа. Работа при изобарическом расширении
для каждого газа равна:
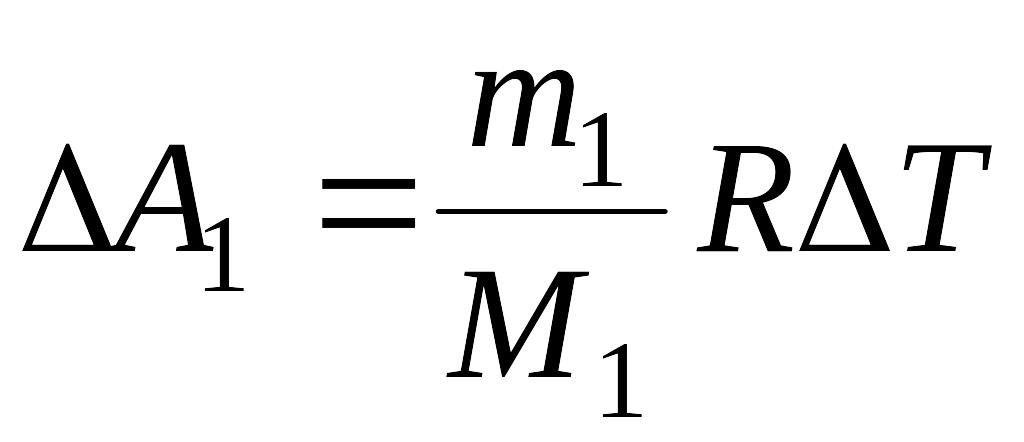 ;
;
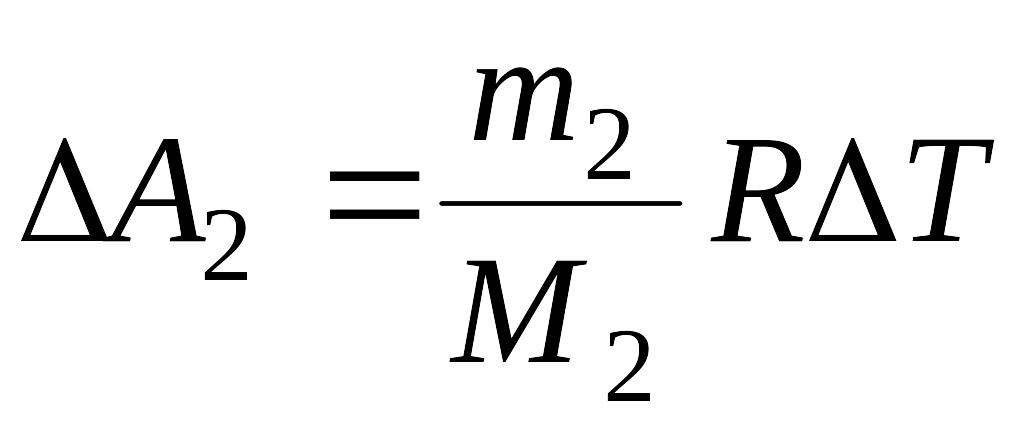 ,
поэтому:
,
поэтому:
 .
.
Подставляя это значение в уравнение (2), получим:
 .
.
Произведем вычисления:
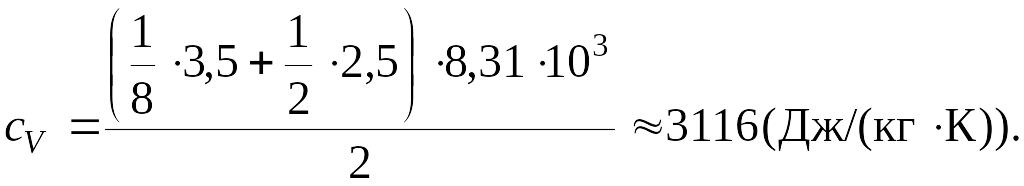
Ответ:
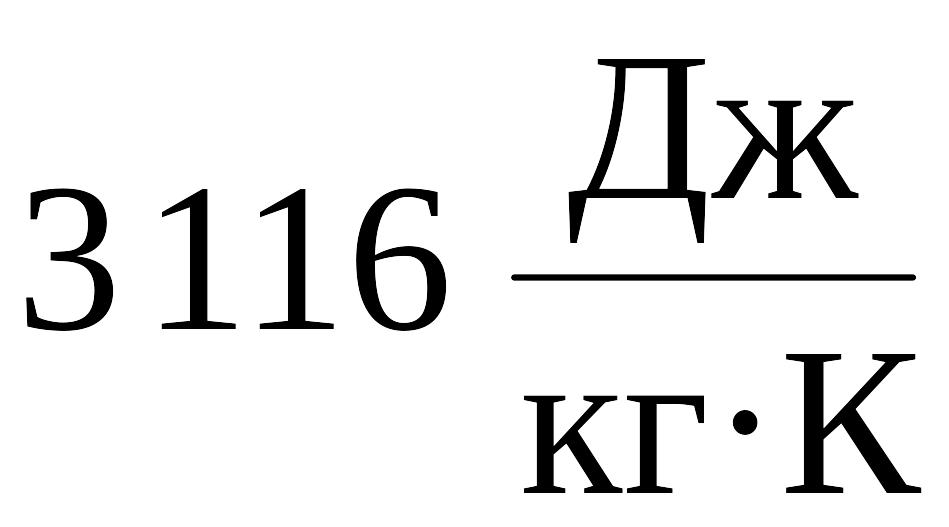 .
.
Задача 22. В цилиндре под поршнем находится водород, который имеет массу 0,02 кг и начальную температуру 27°С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и работу, совершаемую газом. Изобразить процесс графически.
Дано: m = 0,02 кг Т1 = 27°С = 300 К М = 2 кг/кмоль
i = 5 |
Решение: При адиабатном процессе температура и объем газа связаны соотношением:
|
T2 - ? А - ? |
постоянном давлении и постоянном объеме. Для водорода γ = 1,4.
Отсюда выражение для конечной температуры Т2 будет:
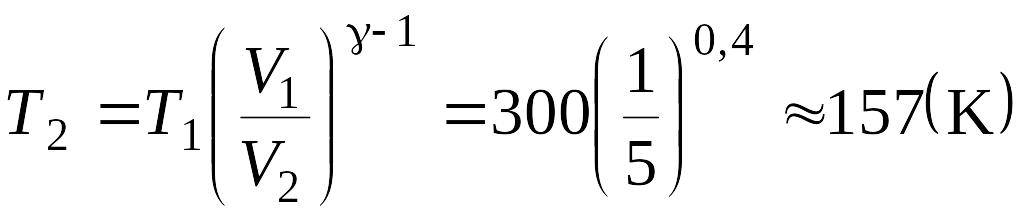 .
.
Работа А1 газа при адиабатическом расширении равна изменению внутренней энергии:
![]() .
.

Работа
А2 газа при изотермическом
процессе может быть выражена в виде:
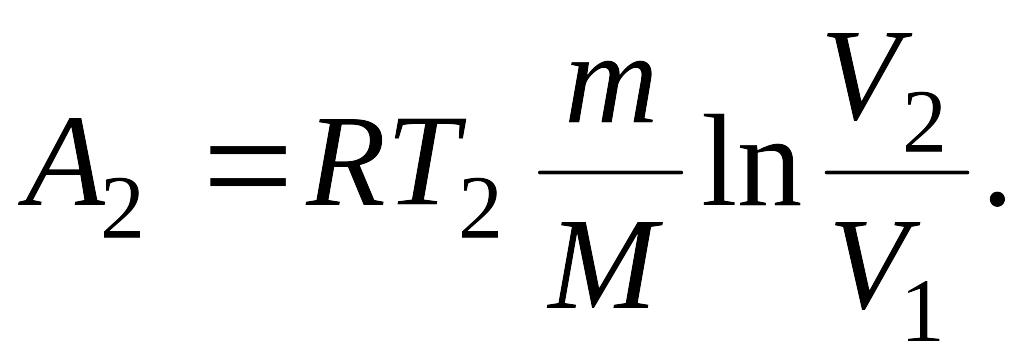
Подставляя известные числовые значения
величин, входящих в правую часть
равенства, и выполняя арифметические
действия, находим:
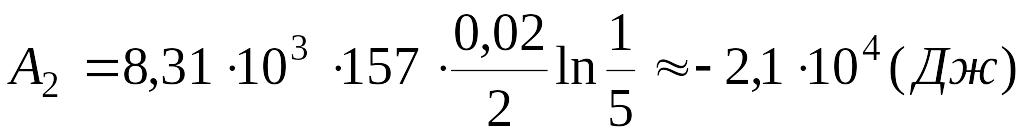 .
.
З нак
«минус» показывает, что при сжатии газа
работа совершается над газом внешними
силами. Полная работа, совершенная газом
при описанных процессах, равна:
нак
«минус» показывает, что при сжатии газа
работа совершается над газом внешними
силами. Полная работа, совершенная газом
при описанных процессах, равна:
![]() .
.
График процесса приведен на рисунке 1.
Ответ: 8,7 · 103 Дж.
Задача 23. Кислород массой m = 2 кг занимает объем V1 = 1 м3 и находится под давлением р1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3 м3, а затем при постоянном объеме до давления р3 = 0,5 МПа. Найти изменение ΔU внутренней энергии газа, совершенную им работу А и количество теплоты Q, переданное газу. Построить график процесса.
Дано: m = 2 кг М = 32 кг/моль V1 = 1 м3 р1 = р2 = 2·105 Мпа V2 = 3 м3 р3 = 5·105 Мпа R = 8,31·10 –3 Дж/(кмоль·К) |
Решение: Изменение внутренней энергии газа выражается формулой:
где i – число степеней свободы молекул газа для двухатомных молекул кислорода (i = 5); М – молярная масса; R – молярная газовая постоянная. |
ΔU - ? А - ? Q - ? |
Начальную и конечную температуры найдем, используя уравнение Менделеева - Клайперона:
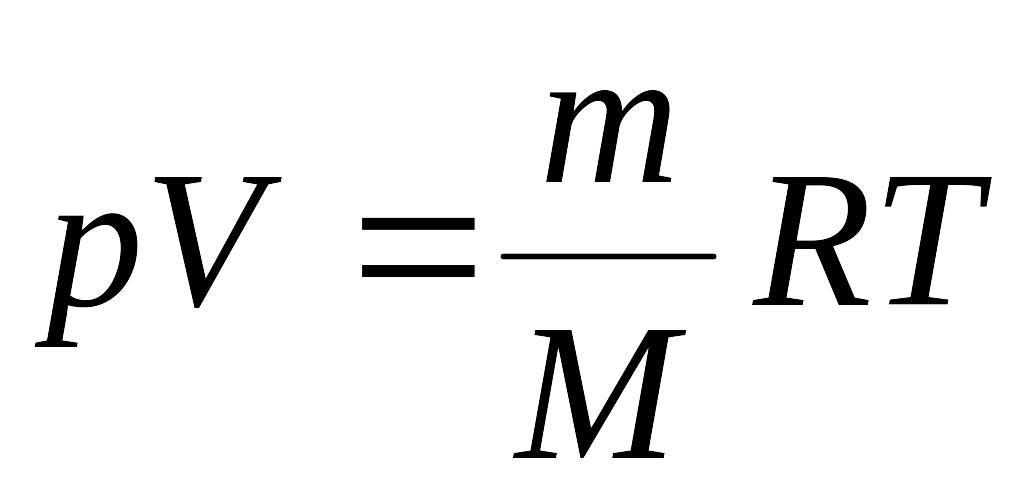 . (2)
. (2)
Решая
его относительно Т,
получим:
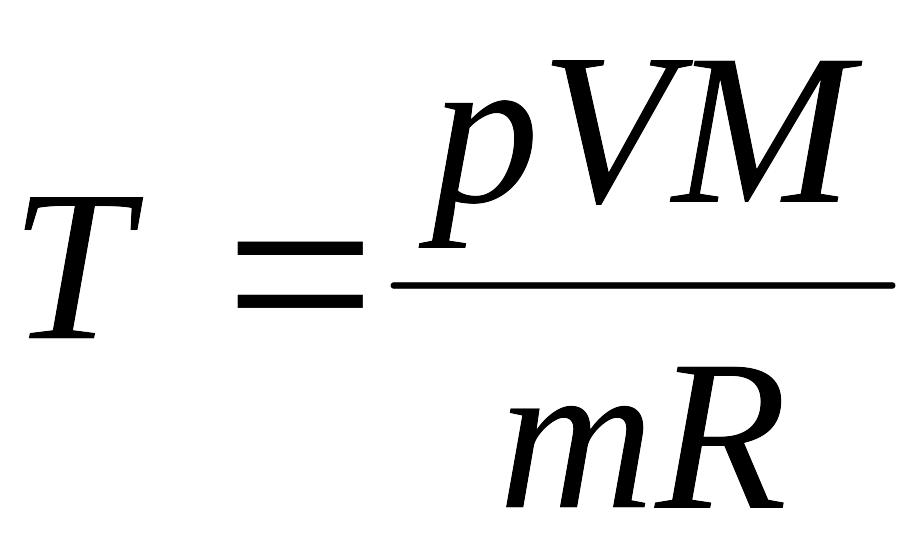 (3)
(3)
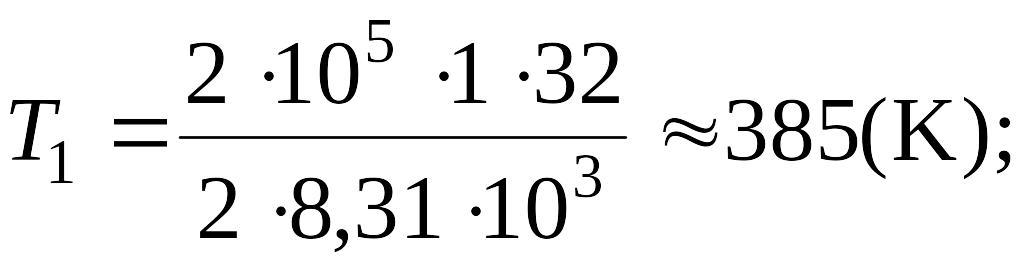
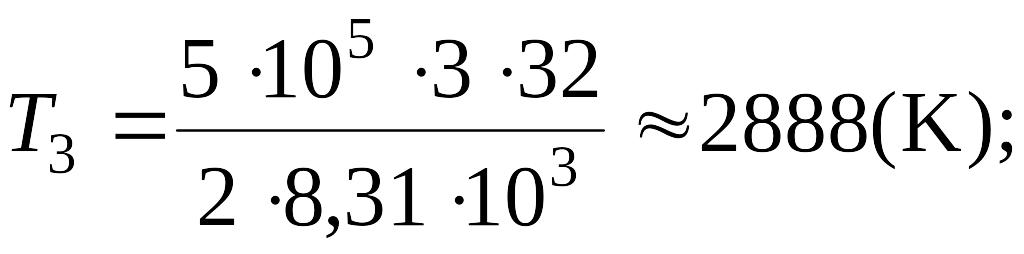
Подставляя в выражение (1) числовые значения входящих в него
величин,
находим:

Работа
расширения газа при постоянном
давлении
выражается формулой:
 .
Подставив числовые значения, получим:
.
Подставив числовые значения, получим:
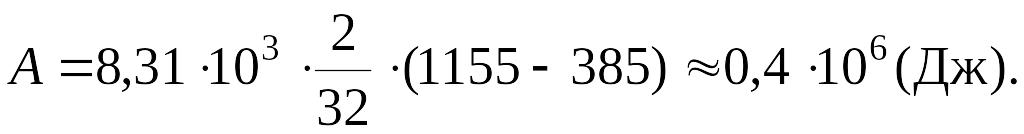
Работа
газа, нагреваемого при постоянном
объеме, равна нулю, т.е. А2
= 0. Следовательно,
полная работа, совершенная газом, равна:
![]() .
Согласно первому началу термодинамики
количество теплоты Q,
переданное газу, равно сумме изменения
внутренней энергии ΔU
и работы А:
.
Согласно первому началу термодинамики
количество теплоты Q,
переданное газу, равно сумме изменения
внутренней энергии ΔU
и работы А:
![]() ,
следовательно:
,
следовательно:
![]() .
.
График процесса приведен на рисунке 2.

Ответ: 3,65 МДж.

 Дано:
Дано: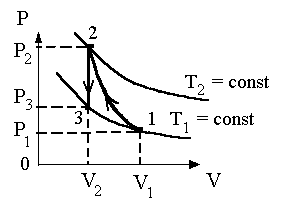
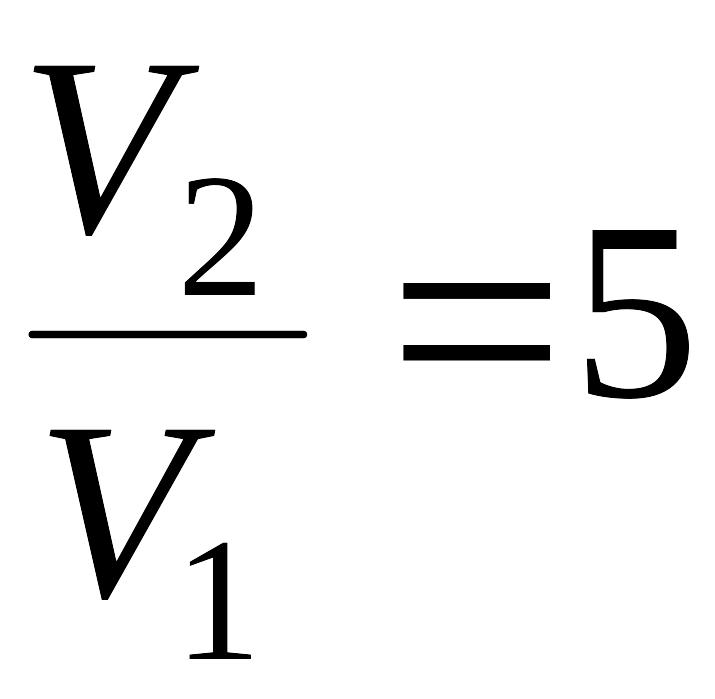
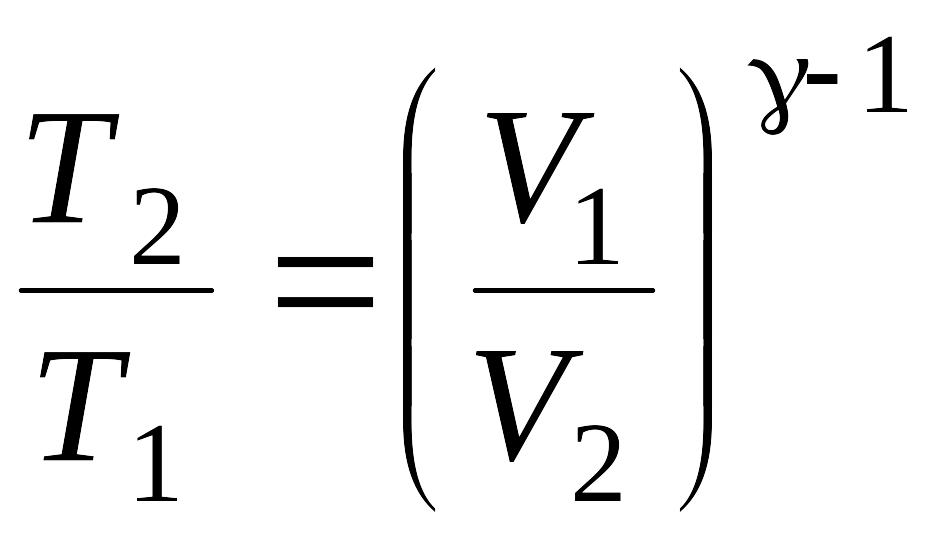 ,
где
,
где
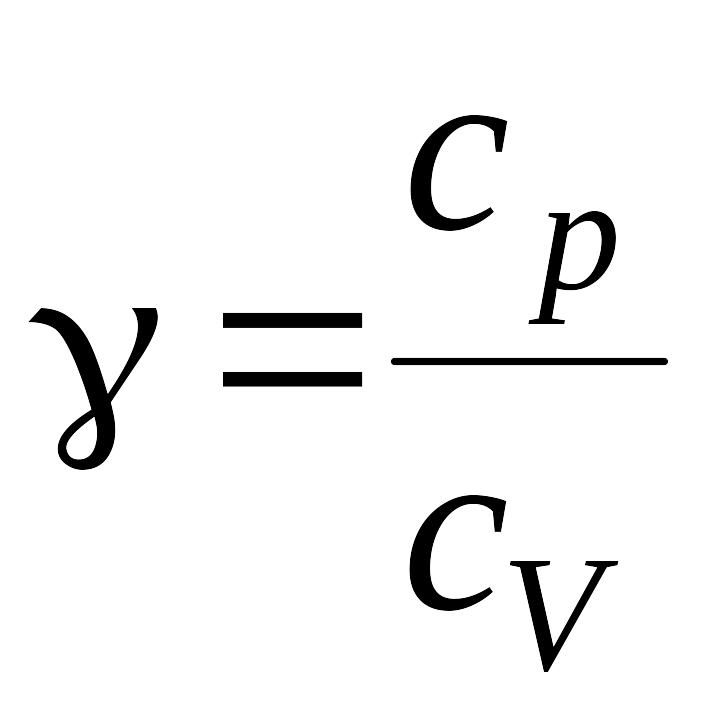 – отношение теплоемкостей газа при
– отношение теплоемкостей газа при
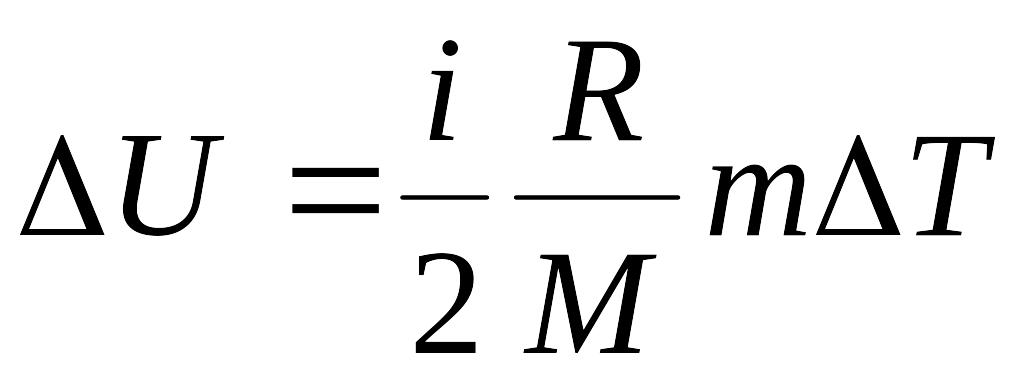 ,
(1)
,
(1)