Контрольная работа №1

Механика.

Молекулярная физика и термодинамика

Номер варианта контрольной работы конкретного студента определяется последней цифрой номера зачетной книжки.

Пример: студенту, имеющему зачетку с номером 20121216, соответствует вариант №6 контрольной работы (этому варианту соответствуют задачи №6 всех тем работы: 1.6, 2.6, 3.6 и т.д.)

1. Кинематика материальной точки

Основные формулы

Средняя скорость тела за промежуток времени Δt определяется отношением перемещения тела Δr к промежутку времени Δt:

где – радиус–вектор начальной точки, – конечной.

Средний модуль скорости тела за промежуток времени Δt есть отношение пути S, пройденного телом за это время, к Δt:

.

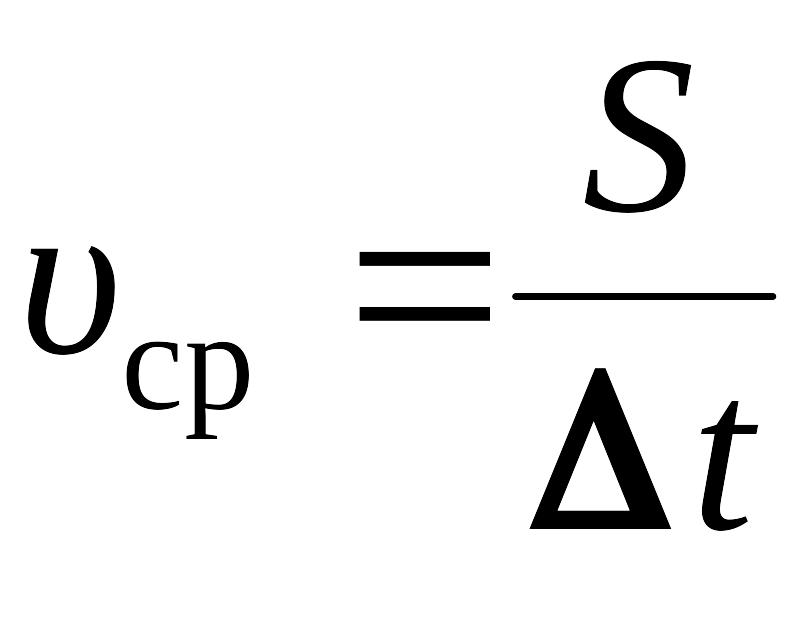Средним ускорением называется отношение изменения скорости ко времени, за которое оно произошло:

.

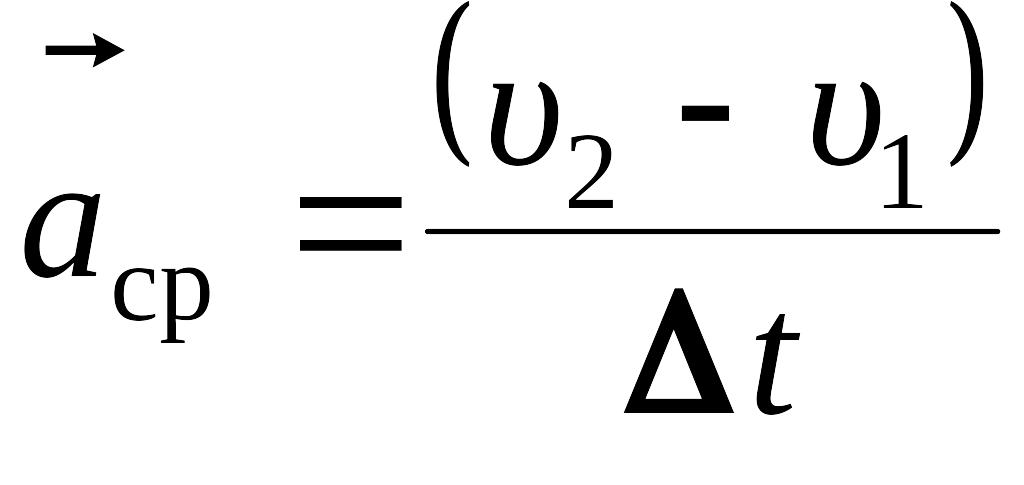Мгновенная скорость равна производной радиус-вектора точки по времени

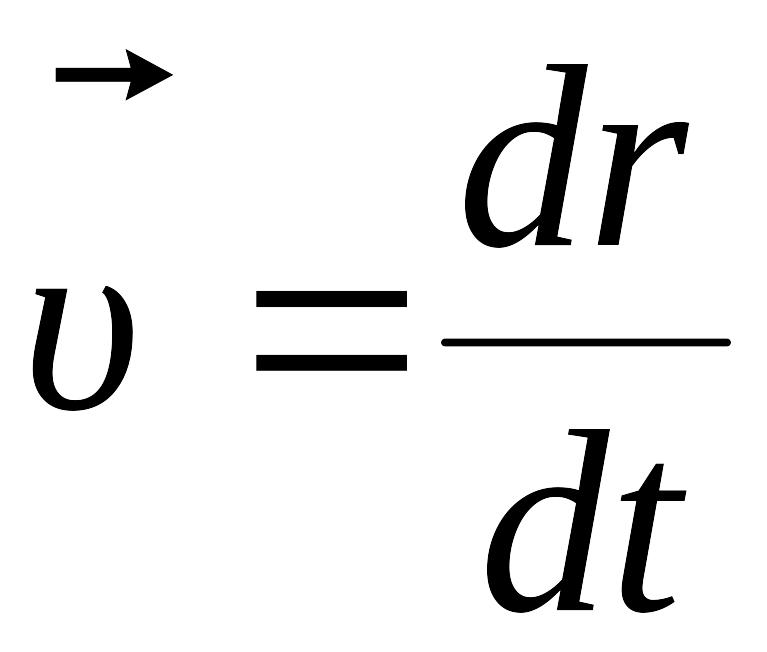
и направлена по касательной к траектории.

Для прямолинейного движения: модуль скорости ,

ускорения .

Кинематические соотношения для прямолинейного равнопеременного движения:

,

,

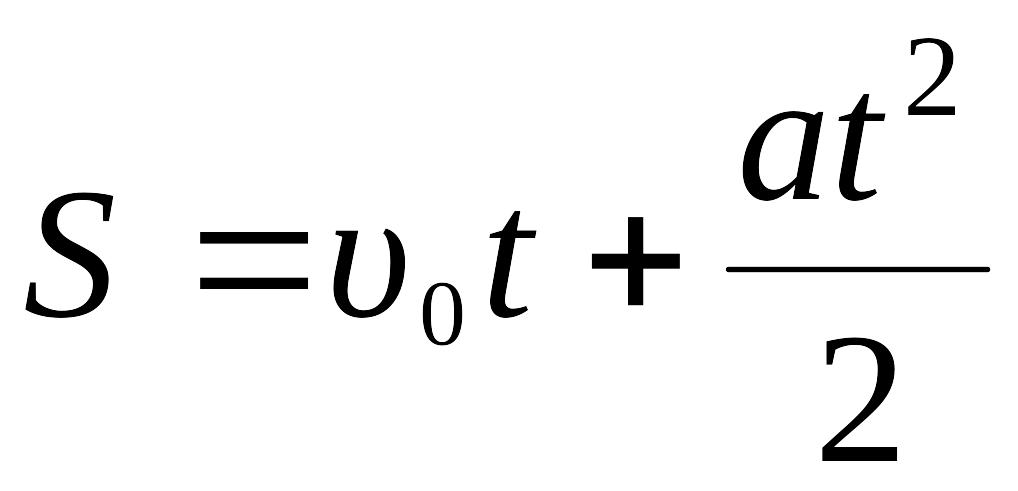где υ₀ скорость тела в момент времени t = 0, a – ускорение тела.

При криволинейном движении полное ускорение тела раскладывается на нормальную и тангенциальную к траектории составляющие: .

Тангенциальная составляющая ускорения определяет изменение модуля скорости: ,

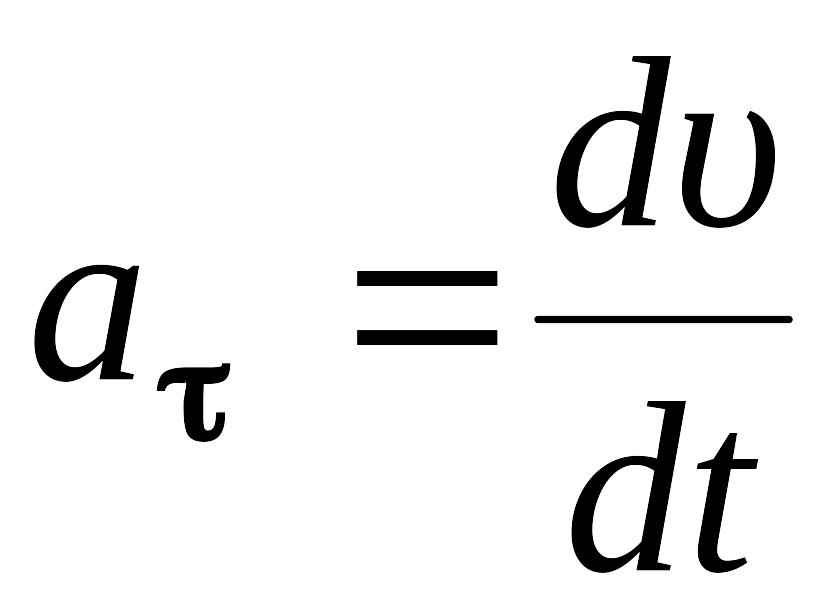нормальная – изменение направления скорости: ,

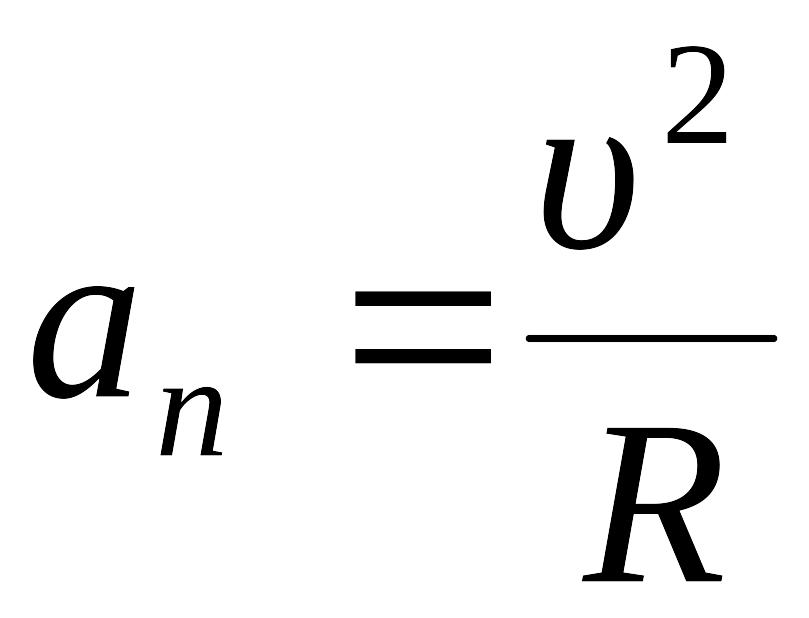где R–радиус кривизны траектории, нормальное ускорение направлено к центру кривизны траектории.

Модуль полного ускорения:

.

При движении по окружности кинематическими характеристиками являются:

– угол поворота φ,

– угловая скорость ω = ,

– угловое ускорение ε = = .

Кинематические уравнения для вращательного равнопеременного движения:

ε t

φ = ω₀ t + ε ,

где ω₀ – угловая скорость в момент времени t=0, e – угловое ускорение.

Линейные и угловые параметры движения связаны соотношением: υ = ω R, a_τ = ε R.

Примеры решения типовых задач

Задача 1.

Тело брошено со скоростью υ₀ = 14,7 , под углом α = 30^о к горизонту. Найти нормальное и тангенциальное ускорения тела через t= 1,25 с после начала движения, а также радиус кривизны траектории в данный момент времени. Сопротивление воздуха не учитывать.

Решение

Полным ускорением является ускорение свободного падения . Оно раскладывается на тангенциальную и нормальную составляющие. Если горизонтальную ось обозначить x, а вертикальную y, то g направленно по оси y, a_τ – по касательной к траектории, а a_n – по нормали к ней. Полная скорость тела направлена по касательной к траектории, её можно разложить на горизонтальную составляющую–υ_x и вертикальную составляющую – υ_y. Треугольники скоростей и ускорений прямоугольные и угол между υ_у и υ такой же, как и между a_τ и g (так как a_τ и υ направлены по касательной к траектории, а υ_y и g – по оси y). Таким образом, чтобы найти a_n и a_τ, нужно определить в данный момент времени υ_x, υ_у, υ.

υ _x = υ₀ cos α = const,

υ _у = - υ₀ sin α + gt

(так как мы выбрали направление оси y вниз),

υ = .

Из подобия треугольников имеем:

= , = ,

отсюда a_τ = g , a_n = g .

Радиус кривизны траектории определяется из условия:

a_n = ,

значит R = = .

Подставив численные значения, получим:

a_τ = 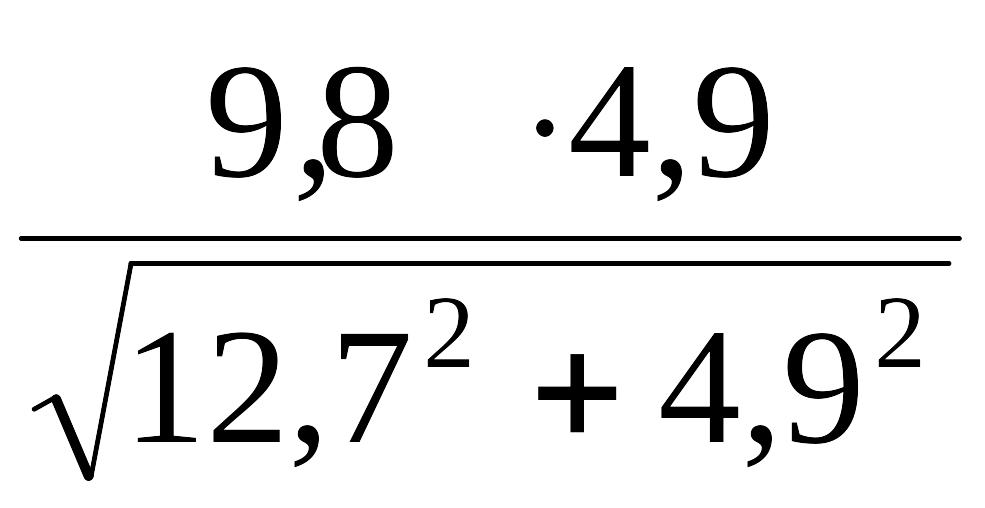= 3,55 ,

a_n = 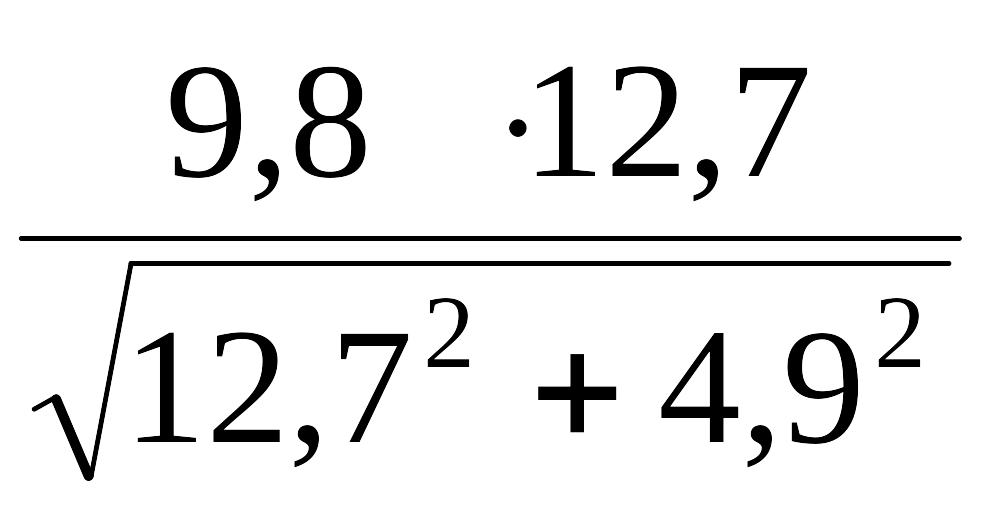= 9,15 ,

R = 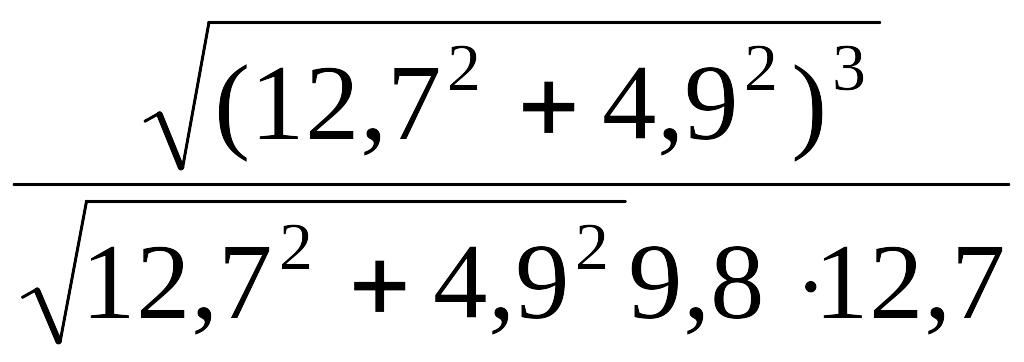= 10 м.

Задача 2

Колесо, вращаясь равнозамедленно, при торможении уменьшило свою скорость за 1 мин с 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов, сделанных им за это время.

Решение

Запишем кинематические соотношения для вращательного движения: ω = ω₀ – ε t, φ = ω₀t – ε .

В условии задана не угловая скорость ω, а частота вращения ν, ω = 2πν, φ = 2πΝ.

Подставляем эти соотношения в уравнения:

2πν = 2πν₀ – ε t.

Отсюда ε = ,

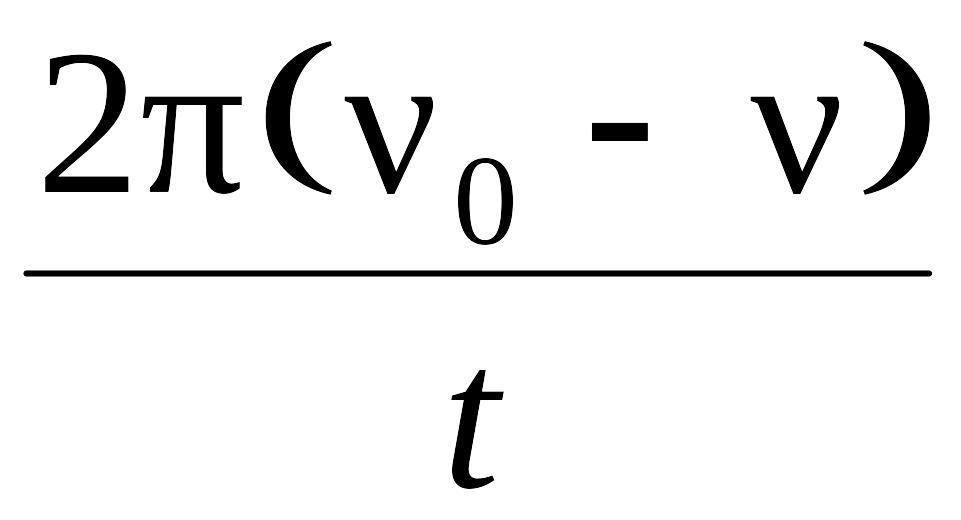2πΝ = 2π ν₀t – ε = 2πν₀t – 2π (ν₀–ν) = 2π (ν₀+ν) ,

или N = (ν₀+ν) .

Подставив числовые значения, найдём:

ε = 750 мин ^-2 = 0,208 с ^-2,

N = 240 оборотов.

Задача 3

Найти угловое ускорение колеса, если известно, что через 2 с после начала равноускоренного движения вектор полного ускорения точки, лежащей на ободе, составляет угол 60^о с направлением линейной скорости этой точки.

Решение

С корость точки направлена по касательной к траектории, т. е. к окружности. По касательной направлено и тангенциальное ускорение. Значит, угол между полным ускорением и тангенциальным ускорением равен углу между ускорением и скоростью.

_­ На чертеже видно, что a_n = a_τ tg α. (1)

Выражаем a_n и a_τ через угловые параметры движения:

a_n = ω²R, a_τ = εR,

и подставляем в (1)

ω²R = ε R tg α. (2)

При нулевой начальной скорости

ω = ε t.

Подставляем в (2):

ε²t² = ε tg α,

ε = = 0,43 с^-2.