1.2. Алгоритм розрахунку
а) Позначають струми у всіх вітках (І1, І2, І3, ..., Іm), вибирають їх напрямок і позначають на схемі стрілками;
б) Складають за першим законом Кірхгофа рівняння для n-1 вузлів;
в) Рівняння, які ще необхідно скласти у кількості m-(n-1), складають за другим законом Кірхгофа, для чого вибирають у колі m-(n-1) взаємно незалежних контурів. Обирають напрямок обходу контурів (за годинниковою стрілкою або проти неї) і відповідно позначають його на схемі.
В результаті отримують систему з m рівнянь. Розв’язання цієї системи дозволяє визначити не тільки числові значення струмів, але і їх дійсний напрямок. Якщо у результаті розв’язку з’явився від’ємний знак для будь-якого струму, то його дійсний напрямок буде протилежним довільно вибраному на початку напрямку.
Таким чином, при розрахунку кіл методом безпосереднього використання законів Кірхгофа складають систему з m+(n-1) рівнянь.
Метод контурних струмів сприяє скороченню числа рівнянь, що вирішуються одночасно з m до m-(n-1):
а) вибирають у схемі взаємно незалежні контури;
б) для вибраних незалежних контурів приймають довільний напрямок контурних струмів;
в) для вибраних контурів складають рівняння за другим законом Кірхгофа відносно контурних струмів.
Після того, як знайдено контурні струми, визначають дійсні струми у вітках. У вітках, що не є суміжними для спільних контурів, знайдений контурний струм буде дорівнювати дійсному струму вітки. У вітках, спільних для суміжних контурів, дійсний струм буде дорівнювати алгебраїчній сумі контурних струмів.
1.3. Приклади розрахунку електричних кіл постійного струму.
П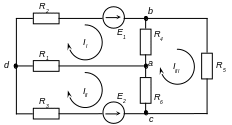
риклад
1.1.
Для електричного кола (рис. 1.1) знайти
струми у всіх вітках методом контурних
струмів і скласти баланс потужності
для цієї схеми, якщо: R1=13
Ом; R2=5
Ом; R3=2
Ом; R4=8
Ом;
R5=11
Ом; R6=15
Ом; Е1=12
В; Е2=16
В.
Рис. 1.1. Електричне коло
Розв’язок. Як видно з рис.1.1, електричне коло складається з трьох контурів. За методом контурних струмів складаємо для цих контурів рівняння падіння напруги з урахуванням того, що напрямки струмів ІІ, ІІІ, ІІІІ співпадають з напрямком руху годинникової стрілки:
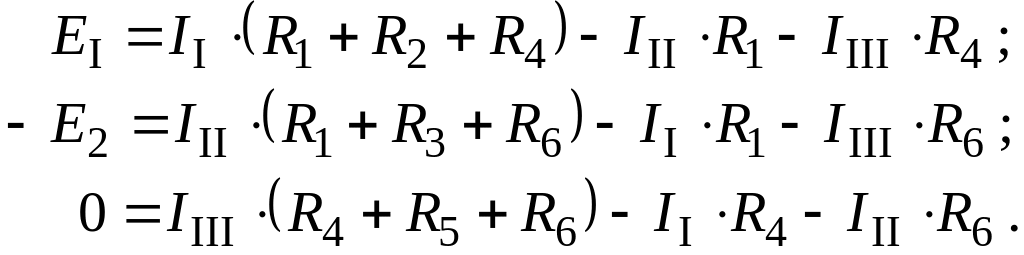(1.1)
Підставимо значення опорів і виконаємо необхідні перетворення:
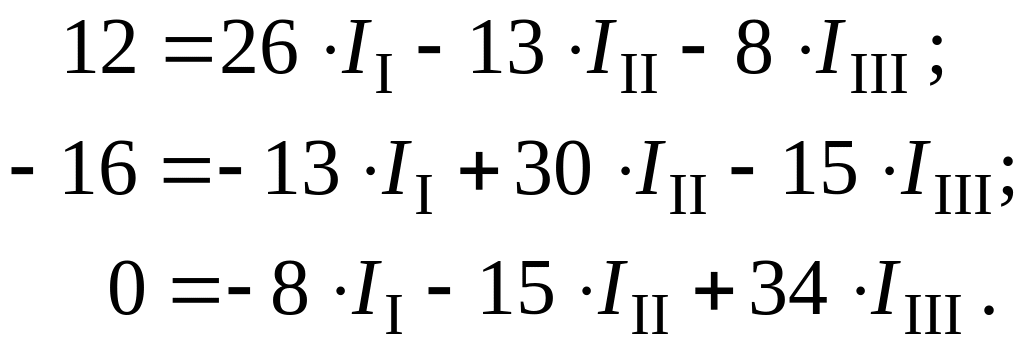(1.2)
З третього рівняння (1.2) визначимо контурний струм ІІІІ і підставимо у перше і друге рівняння (1.2):
;
(1.3)
(1.4)
(1.5)
З рівняння (1.4) визначимо ІІІ і підставимо у (1.5):
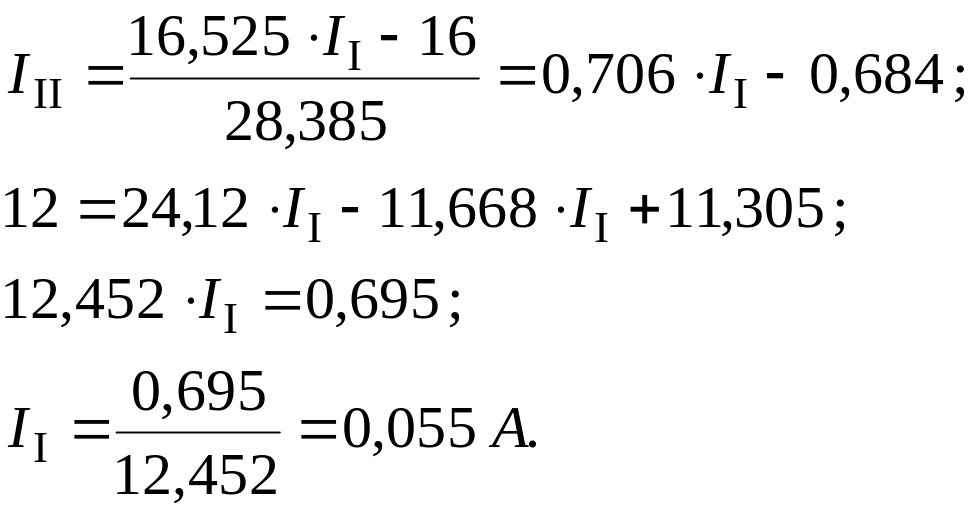(1.6)
Після цього, підставивши значення струму ІІ у (1.6) і значення струмів ІІІ, ІІ у (1.3), визначимо:
На підставі отриманих значень контурних струмів знаходимо струми у вітках електричного кола:
Напрямки струмів у вітках під час розрахунку обираються однаковими.
Розрахунок балансу потужності. Рівняння балансу потужності буде мати вигляд:
,
де n
- номер вітки.
Алгебраїчна сума потужностей всіх джерел енергії (джерел струму і джерел ЕРС або напруги) буде дорівнювати арифметичній сумі потужностей всіх споживачів енергії (резистивних елементів). При цьому потужність джерела необхідно вважати додатньою і записувати в рівнянні із знаком “+”, якщо напрямок струму співпадає з напрямком дії ЕРС. У протилежному випадку цю потужність вважають від’ємною і записують із знаком “–“.
Н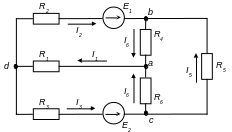
а
рис.1.2 зображено електричне коло з
напрямком струму у вітках і напрямком
ЕРС.
Рис. 1.2. Схема електричного кола
Запишемо для цього кола рівняння балансу потужностей:
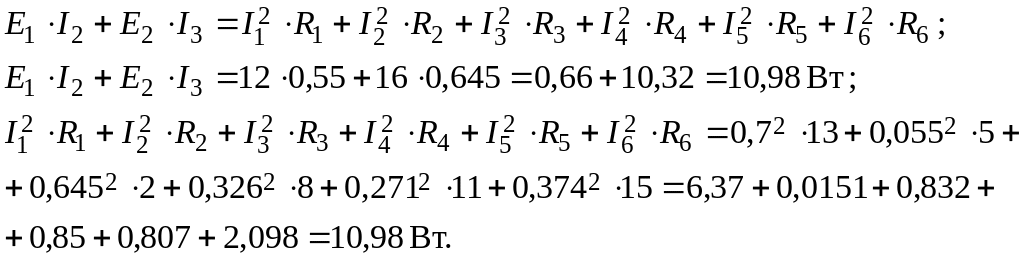
Приклад 1.2. Розглянемо складне електричне коло рис.1.3. Якщо за умовами завдання відомі всі ЕРС і значення опорів споживачів, то необхідно знайти всі струми у вітках електричного кола. Такі задачі розв’язуються за допомогою законів Кірхгофа. В цьому випадку необхідно скласти стільки рівнянь, скільки є невідомих струмів.
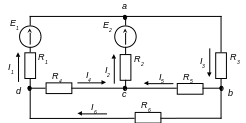
Рис. 1.3. Схема електричного кола
Складемо алгоритм розрахунку:
Якщо коло має послідовні або паралельні зєднання, то його спрощують, замінюючи ці зєднання еквівалентними.
У будь-якому порядку вказують напрямок струмів у вітках. Якщо обраний напрямок струму не співпадає з дійсним, то при розрахунку такі струми будуть із знаком “–“.
Складають n-1 рівнянь за першим законом Кірхгофа (n - число вузлів).
Інші рівняння, яких не вистачає у кількості m-(n-1), де m - число віток, складають за другим законом Кірхгофа. При цьому контур можна обходити як за годинниковою стрілкою, так і проти неї.
За додатні ЕРС і струми приймаються такі, напрямок яких співпадає з напрямком обходу контуру.
Отриману систему рівнянь розв’язують відносно невідомих струмів.
Для електричного кола рис.1.3 складаємо розрахункові рівняння. Довільно вибравши напрямки струмів у вітках кола, складаємо рівняння за першим законом Кірхгофа для а, b, с:
(1.7)
Прийнявши напрямок обходу контурів за годинниковою стрілкою, складаємо рівняння за другим законом Кірхгофа для трьох довільно визначених контурів:
для контуру bасd
(1.8)
для контуру cаdc
(1.9)
для контуру bсdb
(1.10)
Розв’язуючи спільно (1.7) - (1.10), визначаємо струми у вітках електричного кола.
Розв’язок отриманої системи з шести рівнянь - складна операція, тому для розв’язання подібних задач доцільно використовувати метод контурних струмів, який дозволяє зменшити кількість рівнянь. Розглянемо алгоритм розв’язання задачі методом контурних струмів.
Довільно задаємо напрямки контурних струмів у ячейках. Доцільніше вказувати напрямки усіх струмів однаковими, наприклад, за годинниковою стрілкою (рис. 1.4).
Складаємо для кожного контура-ячейки рівняння за другим законом Кірхгофа. Обхід контурів за годинниковою стрілкою:
перший контур
другий контур
третій контур
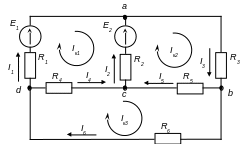
Рис. 1.4. Схема електричного кола
Розв’язуючи спільно рівняння, визначаємо контурні струми. Якщо контурний струм отримуємо із знаком “–“, то це означає, що його напрямок буде протилежним обраному на схемі.
Струми у внутрішніх вітках схеми визначаються як сума або різниця відповідних контурних струмів. В тому випадку, коли контурні струми у вітках співпадають, їх складають, а коли спрямовані назустріч - з більшого віднімають менший.
Струми у зовнішніх вітках кола за своїми значеннями дорівнюють відповідним контурним струмам.
Завдання №1 для самостійної роботи студентів
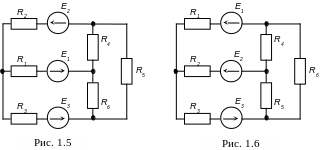
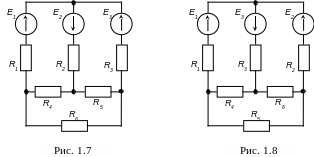
Для електричного кола (рис. 1.5...1.8) по заданим у табл. 1.1 опорам і ЕРС виконати наступне: 1) скласти систему рівнянь, необхідних для визначення струмів за першим і другим законами Кірхгофа; 2) знайти всі струми, користуючись методом контурних струмів; 3) перевірити правильність розв’язання задачі, визначивши всі струми будь-яким іншим методом; 4) скласти рівняння балансу потужностей електричного кола і визначити відповідно значення потужностей джерел і споживачів.
Таблиця 1.1
Дані до розрахунку завдання №1
Номер |
Е1 |
Е2 |
Е3 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
|
Варі-ант |
Рису-нок |
В |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
1.5 |
55 |
25 |
10 |
8 |
4 |
3 |
2 |
5 |
4 |
2 |
1.6 |
40 |
15 |
25 |
4 |
8 |
3 |
5 |
2 |
7 |
3 |
1.7 |
25 |
5 |
35 |
9 |
3 |
2 |
4 |
5 |
5 |
4 |
1.8 |
15 |
25 |
45 |
5 |
2 |
8 |
2 |
2 |
6 |
5 |
1.5 |
20 |
55 |
35 |
4 |
2 |
6 |
3 |
8 |
4 |
6 |
1.6 |
15 |
70 |
30 |
6 |
4 |
3 |
2 |
5 |
3 |
7 |
1.7 |
10 |
60 |
25 |
3 |
5 |
6 |
6 |
3 |
4 |
8 |
1.8 |
20 |
45 |
30 |
4 |
6 |
4 |
4 |
3 |
3 |
9 |
1.5 |
25 |
40 |
15 |
5 |
7 |
2 |
8 |
2 |
3 |
10 |
1.6 |
40 |
65 |
15 |
5 |
10 |
4 |
8 |
10 |
2 |
11 |
1.7 |
35 |
20 |
60 |
9 |
8 |
3 |
6 |
10 |
4 |
12 |
1.8 |
15 |
45 |
70 |
5 |
6 |
6 |
5 |
10 |
5 |
13 |
1.5 |
45 |
100 |
35 |
4 |
4 |
5 |
12 |
6 |
2 |
14 |
1.6 |
25 |
35 |
70 |
3 |
5 |
3 |
5 |
6 |
9 |
15 |
1.7 |
25 |
60 |
44 |
2 |
3 |
8 |
5 |
7 |
8 |
16 |
1.8 |
20 |
40 |
55 |
3 |
2 |
3 |
6 |
8 |
6 |
17 |
1.5 |
75 |
15 |
40 |
6 |
2 |
10 |
4 |
12 |
4 |
18 |
1.6 |
15 |
45 |
60 |
2 |
2 |
4 |
12 |
2 |
3 |
19 |
1.7 |
15 |
30 |
90 |
3 |
2 |
3 |
5 |
4 |
3 |
20 |
1.8 |
35 |
60 |
25 |
4 |
2 |
8 |
11 |
4 |
3 |
21 |
1.5 |
15 |
40 |
35 |
5 |
3 |
4 |
2 |
10 |
3 |
22 |
1.6 |
55 |
25 |
30 |
8 |
3 |
2 |
4 |
2 |
5 |
23 |
1.7 |
35 |
15 |
45 |
3 |
4 |
2 |
3 |
5 |
3 |
24 |
1.8 |
30 |
65 |
10 |
2 |
4 |
2 |
2 |
7 |
3 |
25 |
1.5 |
15 |
30 |
45 |
4 |
5 |
2 |
3 |
6 |
4 |
26 |
1.6 |
30 |
15 |
40 |
2 |
5 |
3 |
2 |
8 |
5 |
Продовження табл. 1.1
Номер |
Е1 |
Е2 |
Е3 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
|
Варі-ант |
Рису-нок |
В |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
27 |
1.7 |
20 |
55 |
20 |
6 |
5 |
3 |
7 |
4 |
5 |
28 |
1.8 |
50 |
10 |
35 |
5 |
6 |
3 |
2 |
4 |
2 |
29 |
1.5 |
40 |
25 |
80 |
3 |
3 |
5 |
4 |
3 |
2 |
30 |
1.6 |
75 |
40 |
30 |
5 |
3 |
4 |
3 |
2 |
10 |
31 |
1.7 |
25 |
45 |
70 |
2 |
4 |
8 |
4 |
10 |
6 |
32 |
1.8 |
55 |
15 |
40 |
8 |
4 |
3 |
2 |
5 |
4 |
33 |
1.5 |
30 |
10 |
25 |
4 |
8 |
3 |
4 |
2 |
7 |
34 |
1.6 |
15 |
55 |
35 |
9 |
3 |
2 |
4 |
3 |
5 |
35 |
1.7 |
15 |
25 |
45 |
5 |
2 |
8 |
2 |
2 |
6 |
36 |
1.8 |
25 |
46 |
30 |
6 |
4 |
3 |
2 |
5 |
3 |
37 |
1.5 |
10 |
60 |
25 |
3 |
5 |
6 |
6 |
3 |
2 |
38 |
1.6 |
60 |
20 |
40 |
4 |
6 |
4 |
5 |
10 |
3 |
39 |
1.7 |
25 |
40 |
60 |
5 |
7 |
2 |
8 |
3 |
10 |
40 |
1.8 |
40 |
75 |
100 |
3 |
10 |
4 |
8 |
5 |
2 |
41 |
1.5 |
45 |
25 |
60 |
9 |
8 |
5 |
6 |
10 |
6 |
42 |
1.6 |
30 |
80 |
45 |
5 |
6 |
7 |
5 |
10 |
4 |
43 |
1.7 |
45 |
65 |
35 |
4 |
5 |
3 |
12 |
6 |
8 |
44 |
1.8 |
15 |
35 |
50 |
3 |
5 |
4 |
5 |
6 |
9 |
45 |
1.5 |
75 |
30 |
45 |
6 |
3 |
8 |
5 |
7 |
5 |
46 |
1.6 |
25 |
40 |
55 |
3 |
2 |
3 |
6 |
8 |
6 |
47 |
1.7 |
75 |
25 |
45 |
6 |
4 |
10 |
3 |
12 |
5 |
48 |
1.8 |
25 |
45 |
60 |
5 |
2 |
4 |
15 |
3 |
4 |
49 |
1.5 |
35 |
20 |
60 |
3 |
2 |
5 |
4 |
5 |
3 |
50 |
1.6 |
30 |
45 |
55 |
4 |
2 |
8 |
10 |
5 |
3 |
51 |
1.7 |
50 |
25 |
15 |
5 |
6 |
4 |
8 |
7 |
4 |
52 |
1.8 |
55 |
35 |
20 |
10 |
5 |
6 |
4 |
3 |
8 |
53 |
1.5 |
15 |
35 |
40 |
8 |
10 |
3 |
5 |
4 |
6 |
Продовження табл. 1.1
Номер |
Е1 |
Е2 |
Е3 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
|
Варі-ант |
Рису-нок |
В |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
54 |
1.6 |
20 |
30 |
45 |
4 |
7 |
5 |
4 |
3 |
2 |
55 |
1.7 |
25 |
30 |
50 |
5 |
6 |
4 |
7 |
2 |
6 |
56 |
1.8 |
30 |
25 |
55 |
10 |
8 |
6 |
4 |
5 |
4 |
57 |
1.5 |
10 |
50 |
35 |
5 |
4 |
3 |
12 |
4 |
2 |
58 |
1.6 |
40 |
15 |
35 |
6 |
3 |
5 |
7 |
6 |
4 |
59 |
1.7 |
45 |
25 |
30 |
3 |
6 |
4 |
5 |
6 |
7 |
60 |
1.8 |
20 |
30 |
60 |
5 |
8 |
10 |
6 |
4 |
2 |
61 |
1.5 |
45 |
20 |
85 |
5 |
6 |
8 |
3 |
4 |
5 |
62 |
1.6 |
100 |
25 |
45 |
15 |
6 |
8 |
4 |
2 |
4 |
63 |
1.7 |
25 |
80 |
15 |
3 |
10 |
7 |
6 |
4 |
5 |
64 |
1.8 |
45 |
35 |
25 |
8 |
7 |
6 |
5 |
2 |
3 |
65 |
1.5 |
75 |
25 |
40 |
6 |
3 |
5 |
4 |
8 |
6 |
66 |
1.6 |
60 |
30 |
20 |
10 |
6 |
5 |
7 |
3 |
2 |
67 |
1.7 |
25 |
35 |
55 |
5 |
6 |
8 |
4 |
2 |
7 |
68 |
1.8 |
10 |
45 |
30 |
2 |
5 |
4 |
10 |
5 |
6 |
69 |
1.5 |
15 |
25 |
10 |
3 |
5 |
2 |
4 |
3 |
5 |
70 |
1.6 |
25 |
20 |
45 |
3 |
2 |
5 |
7 |
3 |
2 |
71 |
1.7 |
50 |
30 |
70 |
6 |
4 |
10 |
6 |
8 |
7 |
72 |
1.8 |
60 |
45 |
50 |
5 |
4 |
3 |
10 |
6 |
8 |
73 |
1.5 |
15 |
10 |
25 |
4 |
2 |
5 |
2 |
3 |
4 |
74 |
1.6 |
40 |
35 |
10 |
4 |
5 |
6 |
7 |
8 |
3 |
75 |
1.7 |
55 |
20 |
35 |
6 |
5 |
7 |
4 |
5 |
3 |
76 |
1.8 |
10 |
25 |
30 |
2 |
4 |
6 |
8 |
10 |
2 |
77 |
1.5 |
40 |
20 |
15 |
8 |
6 |
5 |
4 |
8 |
7 |
78 |
1.6 |
25 |
45 |
15 |
8 |
12 |
7 |
4 |
5 |
6 |
79 |
1.7 |
20 |
45 |
30 |
4 |
3 |
8 |
5 |
6 |
7 |
80 |
1.8 |
25 |
40 |
25 |
5 |
8 |
6 |
10 |
4 |
10 |
Продовження табл. 1.1
Номер |
Е1 |
Е2 |
Е3 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
|
Варі-ант |
Рису-нок |
В |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
81 |
1.5 |
20 |
55 |
35 |
4 |
8 |
6 |
5 |
3 |
4 |
82 |
1.6 |
45 |
70 |
30 |
7 |
10 |
5 |
2 |
4 |
6 |
83 |
1.7 |
15 |
50 |
35 |
3 |
10 |
7 |
4 |
3 |
5 |
84 |
1.8 |
45 |
20 |
70 |
6 |
3 |
8 |
5 |
7 |
2 |
85 |
1.5 |
65 |
20 |
45 |
9 |
7 |
5 |
4 |
3 |
6 |
86 |
1.6 |
60 |
40 |
30 |
10 |
8 |
4 |
5 |
3 |
5 |
87 |
1.7 |
15 |
25 |
45 |
8 |
6 |
3 |
8 |
10 |
2 |
88 |
1.8 |
45 |
15 |
25 |
6 |
7 |
9 |
2 |
5 |
4 |
89 |
1.5 |
25 |
30 |
75 |
3 |
4 |
7 |
4 |
2 |
3 |
90 |
1.6 |
30 |
45 |
10 |
5 |
7 |
8 |
4 |
3 |
6 |
91 |
1.7 |
55 |
10 |
65 |
7 |
3 |
9 |
6 |
5 |
7 |
92 |
1.8 |
15 |
75 |
30 |
3 |
8 |
4 |
6 |
4 |
7 |
93 |
1.5 |
25 |
80 |
40 |
2 |
8 |
5 |
3 |
7 |
6 |
94 |
1.6 |
30 |
55 |
80 |
5 |
10 |
12 |
7 |
8 |
6 |
95 |
1.7 |
95 |
45 |
15 |
11 |
6 |
2 |
5 |
7 |
5 |
96 |
1.8 |
75 |
30 |
40 |
8 |
4 |
6 |
3 |
5 |
7 |
97 |
1.5 |
35 |
35 |
55 |
5 |
3 |
5 |
2 |
4 |
4 |
98 |
1.6 |
40 |
25 |
75 |
6 |
3 |
8 |
5 |
3 |
7 |
99 |
1.7 |
15 |
50 |
35 |
2 |
6 |
3 |
4 |
8 |
5 |
100 |
1.8 |
100 |
50 |
20 |
15 |
5 |
2 |
6 |
7 |
4 |
