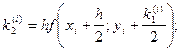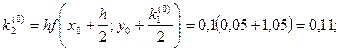Метод Гаусса – Зейделя
Расчетные формулы имеют вид:

т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:
![]()
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.
Расчетные формулы:

k |
x1 |
x2 |
x3 |
точность |
0 |
0 |
0 |
0 |
|
1 |
1.250 |
0.250 |
0.075 |
1.2500 |
2 |
1.106 |
0.321 |
0.132 |
0.1438 |
3 |
1.056 |
0.340 |
0.151 |
0.0500 |
4 |
1.042 |
0.344 |
0.156 |
0.0139 |
5 |
1.039 |
0.346 |
0.157 |
0.0036 |

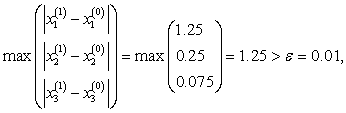


Из
таблицы видно, что нужная точность
достигнута уже на 5–ой итерации вместо
13–ой по методу простой итерации и
значения корней более близки к значениям,
полученным методом обратной матрицы.![]()
6 вопрос: Интерполяция и аппроксимация функции (определение)
Аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию ц(х) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены.
ц(х)- аппроксимирующая функция.
Интерполяция (частный случай аппроксимации)
Если для табличной функции y=f(x), имеющей значение x0 f(x0) требуется построить аппроксимирующюю функцию (x) совпадающую в узлах с xi c заданной, то такой способ называется интерполяцией
7 вопрос: Интерполяционный многочлен Лагранжа (с примером)
|
|
|
|
Интерполяционным многочленом Лагранжа называется многочлен
Этот
многочлен удовлетворяет условиям Узлы
(или полюсы) интерполяции, Интерполяционной формулой Лагранжа называется формула
Формулы (31.1) и (31.2) можно записать так:
Где
Производя
интерполирование функции Отлична от нуля и представляет собой погрешность метода. Эта разность, называемая остаточным членом интерполяции, определяется формулой
В
которой Зависящая
от Пример
31.1. Найти интерполяционный многочлен
Лагранжа, который в точках При Подставляя
в эту формулу заданные значения,
находим
|
8 вопрос: Метод наименьших квадратов ( с примером)
Метод
наименьших квадратов является одним
из наиболее распространенных и наиболее
разработанных вследствие своей простоты
и эффективности методов оценки параметров
линейных эконометрических
моделей. Вместе с тем, при его
применении следует соблюдать определенную
осторожность, поскольку построенные с
его использованием модели могут не
удовлетворять целому ряду требований
к качеству их параметров и, вследствие
этого, недостаточно “хорошо” отображать
закономерности развития процесса
![]() .
.
Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2):
yt = a0 + a1 х1t +...+ an хnt + εt .
Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1 , y2 , ... , yT )' и матрица значений независимых переменных
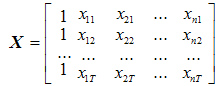
в
которой первый столбец, состоящий из
единиц, соответствует коэффициенту
модели
![]() .
.
Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.
Пример 2.1. Торговое предприятие имеет сеть, состоящую из 12 магазинов, информация о деятельности которых представлена в табл. 2.1.
Руководство предприятия хотело бы знать, как зависит размер годового товарооборота от торговой площади магазина.
Таблица 2.1
Номер магазина |
Годовой товарооборот, млн руб. |
Торговая площадь, тыс. м2 |
1 |
19,76 |
0,24 |
2 |
38,09 |
0,31 |
3 |
40,95 |
0,55 |
4 |
41,08 |
0,48 |
5 |
56,29 |
0,78 |
6 |
68,51 |
0,98 |
7 |
75,01 |
0,94 |
8 |
89,05 |
1,21 |
9 |
91,13 |
1,29 |
10 |
91,26 |
1,12 |
11 |
99,84 |
1,29 |
12 |
108,55 |
1,49 |
Решение
методом наименьших квадратов. Обозначим
—
годовой товарооборот
![]() -го
магазина, млн руб.;
-го
магазина, млн руб.;
![]() —
торговая площадь
-го
магазина, тыс. м2.
—
торговая площадь
-го
магазина, тыс. м2.
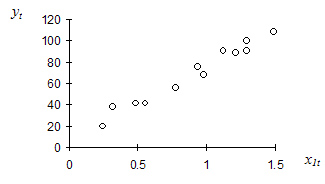
Рис.2.1. Диаграмма рассеяния для примера 2.1
Для определения формы функциональной зависимости между переменными и построим диаграмму рассеяния (рис. 2.1).
На
основании диаграммы рассеяния можно
сделать вывод о позитивной зависимости
годового товарооборота от торговой
площади (т.е. у будет расти с ростом
![]() ).
Наиболее подходящая форма функциональной
связи — линейная.
).
Наиболее подходящая форма функциональной
связи — линейная.
Информация для проведения дальнейших расчетов представлена в табл. 2.2. С помощью метода наименьших квадратов оценим параметры линейной однофакторной эконометрической модели
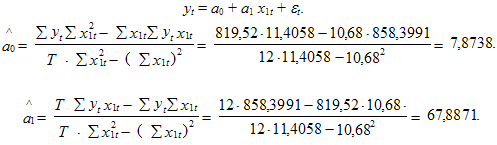
Таблица 2.2
t |
yt |
x1t |
yt2 |
x1t 2 |
x1t yt |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
19,76 |
0,24 |
390,4576 |
0,0576 |
4,7424 |
2 |
38,09 |
0,31 |
1450,8481 |
0,0961 |
11,8079 |
3 |
40,95 |
0,55 |
1676,9025 |
0,3025 |
22,5225 |
4 |
41,08 |
0,48 |
1687,5664 |
0,2304 |
19,7184 |
5 |
56,29 |
0,78 |
3168,5641 |
0,6084 |
43,9062 |
6 |
68,51 |
0,98 |
4693,6201 |
0,9604 |
67,1398 |
7 |
75,01 |
0,94 |
5626,5001 |
0,8836 |
70,5094 |
8 |
89,05 |
1,21 |
7929,9025 |
1,4641 |
107,7505 |
9 |
91,13 |
1,29 |
8304,6769 |
1,6641 |
117,5577 |
10 |
91,26 |
1,12 |
8328,3876 |
1,2544 |
102,2112 |
11 |
99,84 |
1,29 |
9968,0256 |
1,6641 |
128,7936 |
12 |
108,55 |
1,49 |
11783,1025 |
2,2201 |
161,7395 |
S |
819,52 |
10,68 |
65008,554 |
11,4058 |
858,3991 |
Среднее |
68,29 |
0,89 |
|
|
|
Таким
образом,![]()
Cледовательно, при увеличении торговой площади на 1 тыс. м2 при прочих равных условиях среднегодовой товарооборот увеличивается на 67,8871 млн руб.
11 вопрос:
Метод Рунге – Кутта является более точным по сравнению с методом Эйлера. Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора. (См. Формула Тейлора.)
Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге – Кутта учитывает четыре первых члена разложения.
В методе Рунге – Кутта приращения DYi предлагается вычислять по формуле:
Где коэффициенты Ki вычисляются по формулам:
Пример.
Решить методом Рунге – Кутта
дифференциальное уравнение
Для i = 0 вычислим коэффициенты Ki.
Последующие вычисления приводить не будем, а результаты представим в виде таблицы.
Решим этот же пример методом Эйлера. В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения. Однако этот метод дает одновременно и способ нахождения искомой функции в табличной форме.
Применяем
формулу
Производя аналогичные вычисления далее, получаем таблицу значений:
Применим теперь уточненный метод Эйлера.
Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции У на заданном отрезке.
Уравнение
Решение
неоднородного уравнения имеет вид
Общее
решение:
C
учетом начального условия:
Частное
решение:
Для сравнения полученных результатов составим таблицу.
Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001.
|

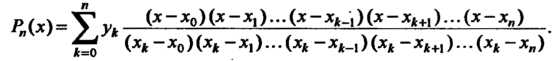 (31.1)
(31.1)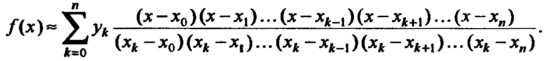 (31.2)
(31.2)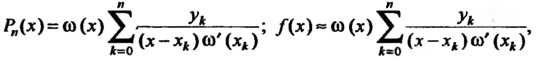
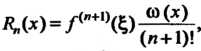

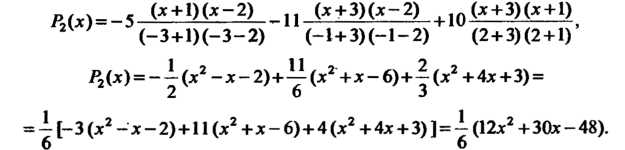 Итак,
Итак,