Тм 7 егж тапсырмасы

АК вектикал білігі (сурет ТМ 7.2.1 –ТМ 7.2.10, кесте ТМ 7)  = 10 с^-1 тұрақты бұрыштық жылдамдықпен айналып тұр. Біліктік А ұшы тесік табанға, ал екінші нүктеге цилиндрлік шарнир арқылы бекітілген (бұл нүкте М 3 кестесінің екінші бағанасында көрсетілген, және де АВ = ВD = DE = ЕК = в). Білікке ұзындығы l₁ = 0,4 м, массасы т₁ = 6 кг ұшына бекітілген 1-ші салмақсыз сырыққа, ұзындығы l₁ = 0,4 м ұшындағы нүктелік массасы т₃ = 6 кг. 3-ші салмақсыз сырық, бірінші сырыққа шарнирлі бекітілген. Білікке массасы т₂ = 10 кг ұзындығы l₂ = 0,6 м біртекті сырық қатты бекітілген. Сырықтардың білікке бекітілген нүктелері кестенің 3 және 4 бағаналарында, ал  бұрышы 5-ші бағанда, β – бұрышы 6-ші бағанада келтірілген.

ТМ 7 мысалы. Тұрақты  бұрыштың жылдамдықпен айналып тұрған АВ білігіне, ұзындығы l, бір ұшы білікке қатты бекітілген екінші ұшына массасы т₁, О₁ D салмақсыз сырығы және ұзындығы l₂, массасы т₂ біртекті О₂ Е – сырығы шарнирге бекітілген. Берілген: в₁ = 0,6 м, в₂ = 0,2 м, в₃ = 0,2 м,  = 60, l₁ = 0,4 м, т₁ = 3 кг, l₂ = 0,33 м, т₂ = 5 кг,  = 5 с^-1.( Сурет ТМ 7.1)

Табу керек: А подшибнигі мен В тесік табан реакцияларын.

Шешуі: АВ білігінен, салмақсыз сырық ОD т₁ жүгімен, шарнир арқылы жалғанған біртекті сырық О₂ Е тұратын механикалық жүйенің реакцияларын табу үшін Даламбер принципін пайдаланамыз. Айналып тұрған білік өсі сәйкестеп, сырықтар Аху координата өсінде жататындай етіп алып, әсер етуші сыртқы күштерді: ауырлық күштері және , тесік табан реакция құраушылары Х_А, У_А және подшипник реакциясын Х_В саламыз.

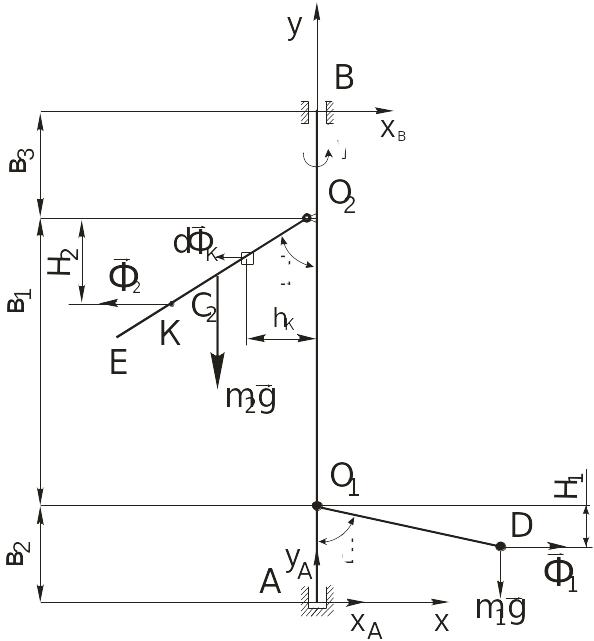
Сурет ТМ 7.1

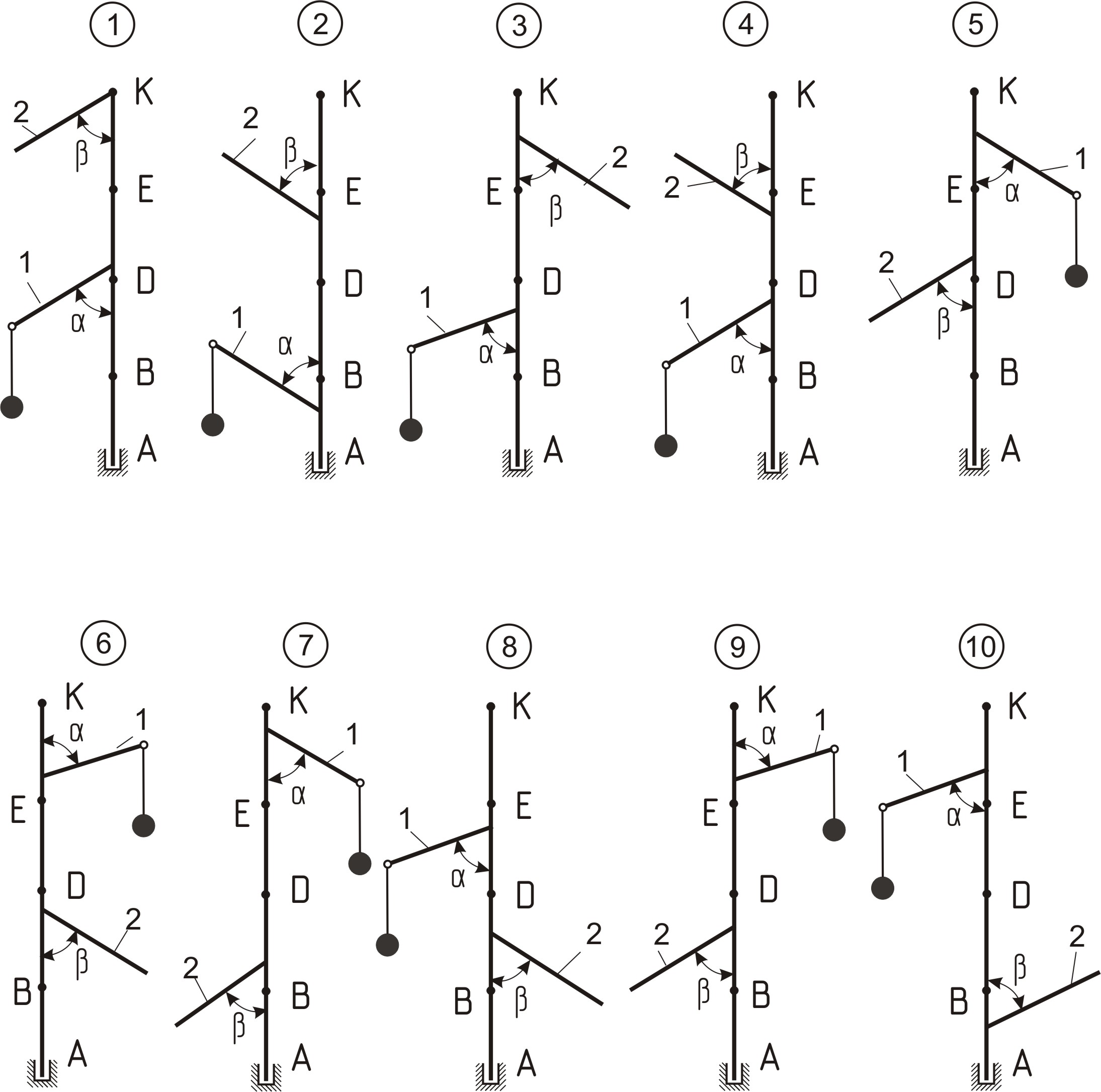
Сурет ТМ 7.2

Кесте ТМ 7

Шарттің нөмірі	Подшипник қойылған нүкте	Сырық 1 бекітілген нүкте	Сырық 2 бекітілген нүкте		βº	Шарт нөмірі	Подшипник қойылған нүкте	Сырық 1 бекітілген нүкте	Сырық 2 бекітілген нүкте		βº
1	2	3	4	5	6	1	2	3	4	5	6
1	В	D	K	30	90	6	D	К	В	30	90
2	D	В	Е	45	75	7	Е	В	К	45	60
3	Е	D	В	60	60	8	К	Е	В	60	45
4	К	D	Е	75	45	9	D	Е	К	75	30
5	В	Е	D	90	30	10	Е	К	D	90	75

Даламбер принципі бойынша бұл күштерге сырықпен жүктің (материальдық нүкте деп) инерциялық күштерін есепке алу керек. Білік бір қалыпты ( = const) айналғандықтан, сырықтың әрбір элементарлық құраушысының нормальдық үдеуі айналу өсіне бағытталған сандық мәні - ға тең, бұндағы h_к – элементарлық құраушының өске дейінгі қашықтығы. Осы себептен инерция күшінің элементарлық құраушысы h_к - пропорциональ W_пк – кері бағытталып, ұшбұрыш заңымен өзгеретін параллель күштер эпюріп береді. Оның тең әсерін -ге алмастырамыз, ал -күш сызығы ұшбырыштың ауырлық центрі арқылы (О₂ нүктесінен қашықтығында) өтеді.

Бізге белгілі кезкелген күш жүйесінің тең әсері, сол жүйеге әсер етуші инерция күштерінің бас векторы, сырық 2 үшін – Ф₂ = т₂ W_С2-ге тең. Бұндағы W_С2 – сырықтың массалар центрінің үдеуі, кезкелген сырық үшін W_С = W_Сп = ² h_С = Сондықтан табамыз.

2-ші сырық О₂ нүктесінде шарнирлі жалғанғандықтан, ол нүктеге қарағанда  т₀ (F_к) = 0; осыдан 2-ші сырық үшін ауытқу бұрышын табамыз.

немесе Ф₂ мәнін есепке алып отырып  бұрышы анықталады.

осы себептен

және де

и

Осылайша жүктің инерциялық күші Ф₁ табамыз, ол айналу өсінен бағытталған, сандық мәні Ф₁ = т₂ ² l₁ sin  = 51,6 Н.

Механикалық жүйеге әсер етуші инерциялық күштер О_ху жазықтығында және тесік табан А мен В подшипнигінің реакциялары, сыртқы ауырлық күштер О_ху жазықтығы екені суретте көрсетілген.

Даламбер принципі бойынша жүйеге түсірілген сыртқы күштер мен инерциялық күштер теңгелген жүйені береді. Сол себептен жазық үшін үш тепе-теңдік теңдеулерін құрамыз:

(1)

(2)

(3) Бұл теңдеуден берілген шамалардың сандық мәні мен табылған шамалардың сандық мәнін қойып; теңдеулер жүйесін шешіп іздеп отырған реакцияларды табамыз:

Есептеу нәтижесі: Х_А = 3,9 Н. У_А = 78,4 Н. Х_В = 68,3 Н.

Мазмұңы
Кіріспе	3
1. ҚАТТЫ ДЕНЕНІҢ ТІРЕК РЕАКЦИЯЛАРЫН ТАБУ	4
1.1 Қатты дене статикасы	4
1.2 Күш моменті мен қос күш	7
1.3 Күш жүйесі	8
1.4 Жазық күш жүйесі	11
1.5 ИМ 1 ЕГЖ тапсырмасы	12
1.6 ИМ 1 мысалы.	14
2 Нүкте кинематикасы.	19
2.1 Нүкте қозғалысының берілу әдістері.	19
2.2. Нүкте жылдамдығы	21
2.3 Нүкте үдеуі	24
2.4 М 2 ЕГЖ тапсырмасы	31
3.Даламбер принципі	36
3.1. Материалдық нүкте мен жүйе үшін Даламбер принципі	36
3.2. Инерция күштерінің бас векторы мен бас моменті	38
3.3 М 3 ЕГЖ тапсырмасы	39
4СОЗЫЛУ – СЫҒЫЛУ	43
4.1 Негізгі түсініктер	43
4.2 ЕГЖ-4 тапсырмасы Статикалық анықталатын жүйелерді баспалдақты сырықты созуға, сығуға есептеу	46
5. Иілгіш жіптерді есептеу	55
5.1 ЕГЖ-5 тапсырмасы	68
6 ҚИМАЛАРДЫҢ ГЕОМЕТРИЯЛЫҚ СИПАТТАМАСЫ	72
6.1 Негізгі түсініктер	72
6.2 Жазық қиманың геометриялық сипатта-маларын анықтау».	75
6.3 Жазық қиманың геометриялық сипаттамасын анықтауға мысал	79
7. БҰРАЛУ	83
7.1. Негізгі түсініктер.	83
7.2 ЕГЖ-5 тапсырмасы М 7. Бұрылғандағы беріктік пен қатандықты есептеу	86
8. ИІЛУ	90
8.1 Негізгі түсініктер	90
8.2 Иілу кезіндегі орын ауыстыруы	92
8.3 8-ЕГЖ тапсырма «Мәткені июге есептеу»	94
9ОРНЫҚТЫЛЫҚ	110
9.1. Негізгі түсініктер	110
9.2. Орнықтылыққа есептеуге мысал	113
9.3 9-ЕГЖ тапсырма «Орнықтылыққа есептеу»	116
0. ЖЕТЕКТІ КИНЕМАТИКАЛЫҚ ЕСЕБІ	119
0.. Электрқозқалтқышты таңдау	121
10.3 ЕГЖ М10 тапсырма. Тісті берілісті есептеу	124
10.4 ЕГЖ М10 Редукторлы берілісті есептеу мысалының шешуі	128
Кинематикалық есептеу	128
Әдебиеттер	132
Қосымшалар	134

Оразбеков Нурдаулет Балтабайұлы

Сәңкібаев Темирхан Ебейсинұлы