Тм 5 егж тапсырмасы

Материалдық нүкте қозғалысының дифференциальдық теңдеуіне интегралдау

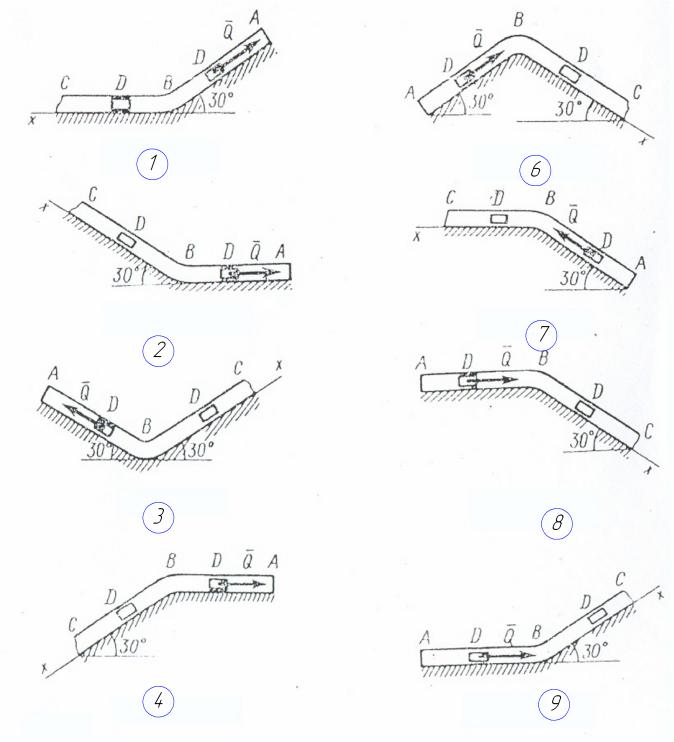
Массасы т – D жүгі А нүктесіне V₀ жылдамдығымен қозғалып вертикаль жазықта жатқан АВС иілген трубасымен қозғалады. Трубаның екі аралығында көлбеу, немесе біреуі горизонталь, ал екіншісі көлбеу аралықтар (ТМ 5.1.1-ТМ 5.1.10 суреті мен ТМ 5 кестесі). АВ аралығындағы трубадағы жүкке оның ауырлық күші мен тұрақты күші әсер етеді (оның бағыты суретте көрсетілген) және ортаның кедергі күші жылдамдығына пропорциональді (қозғалыс бағытына қарсы бағытталған).

Жүк В нүктесінде жылдамдығын сақтап трубаның ВС аралығында, ауырлық күшінен басқа айнымалы күш әсерінен, бұл күштің х өсіндегі проекциясы F_х кестеде берілген, қозғалады.

Жүкті материалдық нүкте деп, АВ = l аралығын немесе бұл аралықты жүріп өткен уақыта t₁ белгілі деп алып, трубаның ВС аралығындағы х = f (t), бұнадығ х = ВD заңдылығын табу керек. Жүкпен труба аралығындағы үйкелісті есепке алмау керек.

ТМ 5 кесте

Шарт нөмірі	т, кг	V0, м/с	Q, H	R, H	l, м	t1, c	Fx, H
1	2,4	12	5	0,8 V2	1,5	–	4 sin (4 t)
2	2	20	6	0,4 V	–	2,5	– 5 cos (4 t)
3	8	10	16	0,5 V2	4	–	6 t2
4	1,8	24	5	0,3 V	–	2	– 2 cos (2 t)
5	6	15	12	0,6 V2	5	–	– 5 sin (2 t)
6	4,5	22	9	0,5 V	–	3	3 t
7	4	12	10	0,8 V2	2,5	–	6 cos (4 t)
8	1,6	18	4	0,4 V	–	2	– 3
9	4,8	10	10	0,2 V2	4	–	4 cos (2 t)
10	3	22	9	0,5 V	–	3	4 sin (2 t)

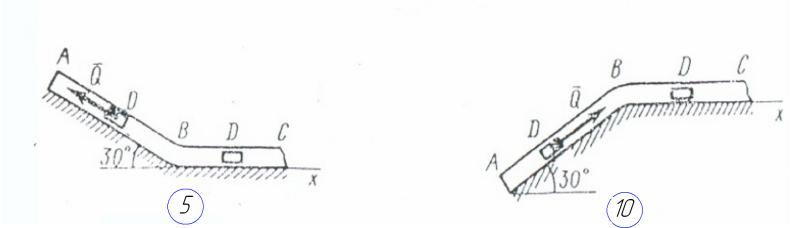Сурет ТМ 5.1

Нұсқау. ТМ 5 есебі – материалдық нүктесінің дифференциалдық теңдеуін интегралдауға арналған (динамиканың екінші есебін шешу). Есептің шешімін екі бөліктен тұрады. Ең алдымен (жүктің) нүктенің АВ аралығындағы дифференциалдық теңдеуін құрып, айнымалары бөлінетін дифференциалдық теңдеуін интегралдып, бастапқы шартты пайдаланып, АВ аралығының қашықтығын, немесе жүріп өтетін уақытын пайдаланып, ВС аралығын жүк қандай жылдамдықпен бастап қозғалатын анықталады. Осыдан кейін ВС аралығындағы жүк қозғалысының дифференциалдық теңдеуін құрып, уақыт t = 0 болғанда жүк В нүктесінде тұр, ал жылдамдығы V_B – ға тең деп алынады. Егер АВ аралығының ұзындығы l белгілі болса, нүкте теңдеуінің қозғалысын айнымалы шаманы жол S деп өрнектеген ыңғайлы

ТМ 5-ші мысал. Вертикаль жазықтықта орналасқан (ТМ 5.2 сурет) АВ брубасының вертикаль аралығында, массасы т D жүгі ауырлық күші мен ортаның кедергісі әсерінен қозғалады; А нүктесі мен В нүктесіндегі аралық l-ге тең, А нүктесіндегі жылдамдық V_А = V₀ – ге тең. Трубаның ВС көлбеу аралығында жүкке ауырлық күші мен F = F (t) (өлшем бірлігі Н) айнымалы күш әсерінен қозғалады.

Берілгені: т = 2 кг, R = μ V², бұндағы μ = 0,4 кг/м, V₀ = 5 м/с, l = 2,5 м, F_х = 16 sin (4 t).

Табу керек: х = f (t) жүктің ВС аралығындағы қозғалу заңын.

Шешу. 1. АВ аралығындағы жүктің қозғалысын, жүкті материалдық нүкте деп қарастырамыз. Жүкті (аралықтың кезкелген жерінде) орналастырып және әсер етуші күштерді және саламыз. АS өсін жүргізіп, осы ось бойындағы жүктің қозғалысын дифференциалдық теңдеуін құрамыз:

және (1)

Осыдан соң табамыз: Р_S = P = mq, R_S = – μ V²; бұл теңдеудегі айнымалы күштерді қандай айнымалығы байланысты екенін көрсету керек. V_z = V, екенін ескере отырып, табамыз

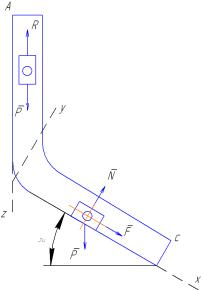
Сурет ТМ 5.2

или (2)

Мынадай қысқаша белгілер еңгізсек:

(3)

бұнда есептеу үшін g ≈ 10 м/с² деп алынған. Осылардан кейін (2) теңдеуді мына түрде жазуға болады

(4)

Теңдеу (4) өзара бөлінетін айнымалар, екі жағын интегралдап, табамыз

или . (5)

Бастапқы шарт бойынша z = 0, V = V₀, осы себептен , (5)-ші теңдіктен табамыз немесе

Осы себептен

и .

Осылар нәтижесінде

. (6)

(6) өрнекте z = l = 2,5 м және к мен п (3) өрнектегі шамалармен алмастырып V_B нүктесіндегі жылдамдықты табамыз В (V₀ = 5 м/с, е = 2,7):

и V_B = 6,4 м/с. (7)

2. енді жүктің ВС аралығындағы қозғалысын қарастырамыз. Тойылған V_B осы аралық үшін бастапқы жылдамдық болып есептеледі (V₀ = V_B). Жүкті (аралықтың кезкелген жерінде) орналастырып әсер етуші күштерді саламыз: ауырлық күші и

В нүктесінен Вх өсін жүргізіп осы өске қарағандағы жүк қозғалысының дифференциалдық теңдеуін жазамыз:

(8)

Бұнда Р_х = Р sin 30º = 0,5 mg, N_х = 0; F_x = 16 sin (4t), осы себептен (8) теңдеу мына түрге келеді

(9)

Теңдіктің екі жағында т = 2 кг бөліп, g ≈ 10м/с² деп алып, бұл теңдеуді мына түрге келтіреміз:

(10)

Теңдеудің (10) екі жағында dt көбейтіп, сосын интегралдан, табамыз

V_x = 5 t – 2 cos (4 t) + C₂. (11)

Уақытты жүк В нүктесінде тұрған сәттен есептеп V₀ = V_В = 6,4 м/с, t = 0. бұл шамаларды (11) өрнекке қойып, табамыз

Бұл табылған С₂ шамасын (11) теңдеуін қойып, табамыз

(12)

Теңдеудің екі жағында dt көбейтіп, сосын интегралдап, табамыз

х = 2,5 t ² – 0,5 sin (4t) + 8,4 t + C₃. (13)

Бізге белгілі t = 0: х = 0, сондықтан С₃ = 0, осы себептерден іздеп отырған жүк қозғалысының теңдеу (13) теңдіктен шығады.

х = 2,5 t ² + 8,4 t – 0,5 sin (4t). (14)

бұнда х – мертмен, t – секундпен өлшенеді.