Тм 3 егж тапсырмасы

М нүктесі Оху жазықтығында қозғалыста (сурет ТМ 3.2.1- ТМ 3.2.10, кесте ТМ 3, нүкте тракториясы суретте шартты түрде салынған). Нүкте қозғалы-сының заңы мына теңдеулер х = f₁ (t), у = f₂ (t), бұнда х және у сантиметр, t – секунтпен берілген.

Нүкте траекториясының теңдеуін табу керек; уақыт t₁ = 1с болған сәттегі нүкте жылдамдығы мен үдеуін, және де нүктенің жанама, нормальдық үдеулерін, уақытқа сәйкес сәтіндегі нүкте траекториясының қисықтық радиусын табу керек.

Заңдылық х = f₁ (t) сурет жазылу арқылы, ал заңдылық у = f₂ (t) ТМ 3 кестесінде (сур. 1-3 үшін 2-ші бағана, сур. 4-7 үшін 3-ші бағана, сур. 8-10 үшін 4-ші бағанада берілген). Сурет реті ТМ 3 кестесінде – ең соңғы санға сәйкес.

Мысал ТМ 3. Оху жазықтығындағы нүктенің қозғалыс заңдары берілген:

(х, у – сантиметрмен, t – секунтпен берілген).

Нүкте траекториясының теңдеуін табу керек; уақыт t₁ = 1 с болғанда нүкте жылдамдығы мен толық, нормальдық және жанама үдеуін, траекториясының көрсетілген сәттегі қисықтық радиусын анықтау қажет.

Шешуі. 1. Нүкте траекториясының теңдеуін табу үшін берілген теңдеулерден уақыттын айырамыз. Уақыт t тригонометриялық функциялардың аргументіне кіріп тұрғандықтан, және де бір аргумент екіншісінен екі есе артық болғандықтан тригонометриялық формуланы пайдаламыз.

cos 2  = 1 – 2 sin²  немесе (1)

берілген қозғалыс теңдеулерінен сәйкес функцияларды тауып (1) теңдікке қойып, табамыз

сондықтан

Сурет ТМ 3.1

Осыдан нүкте мынадай траектория теңдеуін табамыз (параболла, сурет ТМ 3.1):

(2)

2. Уақыт t = 1 с болған сәттегі нүктенің М₁ (х_1, у₁) орнын табамыз:

Нүкте жылдамдығы оның координаталар бойымен проекциялары арқылы анықтаймыз:

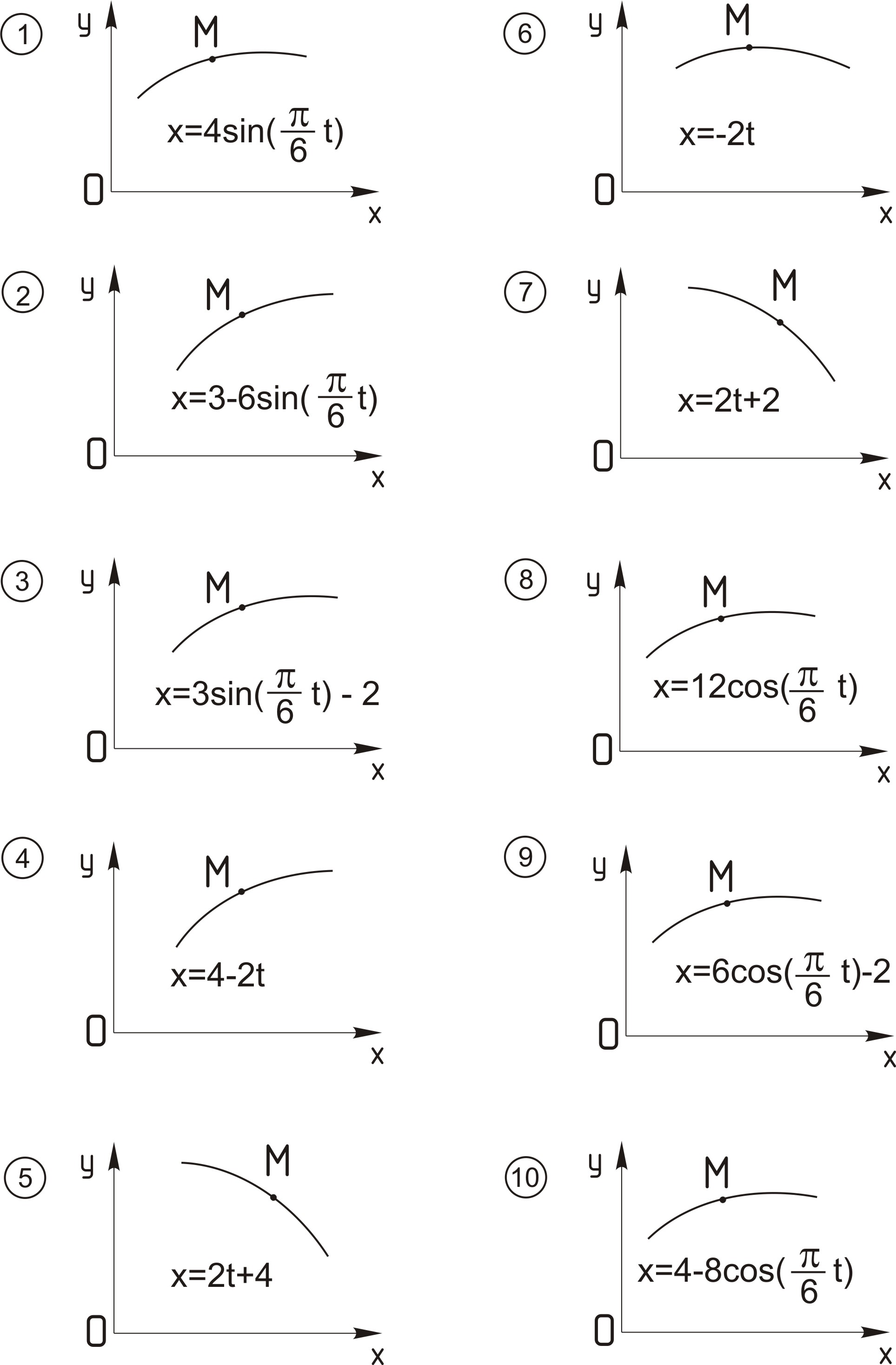
Сурет ТМ 3.2.

ТМ 3 кестесі

Шарт нөмірі	у = f2 (t)
	сур. 1-3	сур. 4-7	сур. 8-10
1	2	3	4
1		(t – 2)2	– 6 cos ( )
2	2 – 6 cos ( )
3		(4 + 2 t)2
4		2 (t +1)2
5
6		3 (t +1)2 – 2
7		(t +1)3
8
9		2 t3
10

уақыт t = 1с.

V_1x = 2,23 см/с, V_1у = 0,72 см/с, V₁ = 2,24 см/с. (3)

3. Нүкте үдеуін де осылайша табамыз:

және уақыт t = 1с болғанда

(4)

4. Теңдікті уақыт бойынша дифференциалдан нүктенің жанама үдеуін табамыз:

осыдан (5)

(5)-ші өрнектің оң жағындағы шамалардың сандық мәні (3) және (4) теңдіктерде берілген. Бұл мәндердің сандық мәнін (5)-ші өрнекке қойсақ, t = 1 с болғанда W_1 = 1,63 см/с².

5. Нүктенің нормальдық былайша анықталады Бұл өрнекке W₁ және W_1, сандық мәндерін қойсақ, t = 1 с, болғанда W_1п = 0,66 см/с² болады.

6. Траекторияның қисықтың радиусы Бұл өрнекке V₁, және W_1п – сандықдың мәндерін қойсақ t = 1 с,  = 8,3 см табамыз. Табылған мәндерде ескере отырып схема түрінде ТМ 3.1 суретін саламыз. Бұнда М₁ С = ₁.