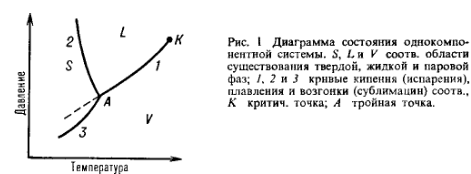
Приложение правила фаз Гиббса к однокомпонентным системам. Диаграммы состояния воды и серы.
В качестве примера рассмотрим однокомпонентную систему – воды. Если имеем одну фазу, например, пар, то в этом случае система имеет две степени свободы, так как состояние газа характеризуется тремя переменными: температурой Т, давлением Р и объемом V, но из них только два являются независимыми, так как уравнение состояния РV = nRТ связывает их с третьей. При равновесии воды с паром и льдом в системе не имеется ни одной степени свободы, так как это состояние строго характеризуется определёнными значениями температуры и давления:
Р = 4,575 мм рт.ст., Т = 0,0076 оС.
Лекция №24
Приложение правила фаз Гиббса к двухкомпонентным системам
Согласно правилу фаз f = n + 2 – k, для системы из двух компонентов f = 0, когда k=4, т.е. число равновесных соприкасающихся фаз не может быть больше 4, а число степеней свободы можем изменить от 0 до 3 (когда k=1, то f = 3). Двухкомпонентная система может быть наглядно представлена или пространственной диаграммой состояния, координатами которой будут температура, давление и состав или сложной ее проекцией на плоскость.
При пространственном изображении диаграммы двухкомпонентной системы пользуются пространственной системой координат. На одной оси откладывают температуру, на другой – давление Р, на третьей – концентрацию С. Существование каждой фазы системы изображается вполне определённым объемом в пространстве координат. Для практических целей часто пользуются диаграммами – состав – свойство. Одну из переменных – давление или температуру – принимают за постоянную величину, и, таким образом, состояние двухкомпонентной системы изображается уже не в пространстве, а на плоскости. Так как одну из переменных величин принимаем за постоянную, то это уменьшает возможное число степеней свободы на единицу. Поэтому уравнение правила фаз будет иметь следующий вид:
f = n + 1 – k
Для изображения диаграммы состав – свойство пользуются прямоугольными системами координат, на оси абсцисс откладывают состав, а на оси ординат – свойство (давление, температуру) 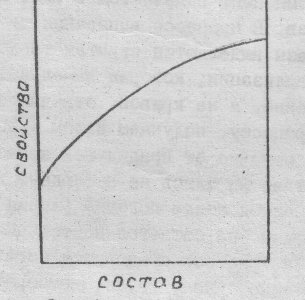(рис.1).
Рис.
1.
Лекция № 3
Свойства растворов и гетерогенных систем
1.Общая характеристика. Концентрация растворов
Растворы имеют огромное значение в медицине:
Химические превращения, протекающие в животных, растительных организмах, осуществляются в растворах
Внутренняя среда организма: кровь, лимфа, слюна, различные тканевые жидкости – растворы
Природная, минеральная, питьевая воды – растворы
Многие лекарственные формы, также – растворы (настойка йода, нашатырный спирт, растворы глюкозы, соляной кислоты и др).
Растворами называются фазы переменного состава.
Растворы – это однородные смеси молекул, атомов или ионов веществ, между которыми имеется физическое, а нередко и химическое взаимодействие.
На химическое взаимодействие указывает гидратная теория Д.И. Менделеева. Доказательством химического взаимодействия в растворах являются тепловые эффекты при растворении и образование гидратированных соединений.
Простые составные части, смешением которых образуются растворы любого возможного состава называют компонентами раствора.
Деление компонентов на растворитель и растворенное вещество является достаточно условным. Растворителем обычно называют компонент, находящийся в избытке по сравнению с другими компонентами, либо это жидкий компонент, если остальные компоненты – газы или твердые вещества. Растворитель обычно называют первым компонентом, а растворенное вещество – вторым, третьим и т.д.
Важнейшей характеристикой раствора является его состав. Состав раствора можно выразить через массовые, oбъeмные, молярные и другие количества компонентов.