Лабораторная работа № 4

4.1. Определение прогибов и углов поворота сечений балки на шарнирных опорах

Цель работы: Проверить формулы для определения прогибов и углов поворота сечений балки по методу Верещагина.

Оборудование и инструменты: Установка СМ-5, штатив, индикатор часового типа 0-10 мм, набор гирь 0.5-1 кг, штангенциркуль, измерительная линейка.

Теоретические предпосылки. Определение перемещений в системах, состоящих из прямолинейных элементов постоянной жесткости, можно значительно упростить путем применения приема вычисления интеграла Мора, называемого способом перемножения эпюр или методом Верещагина. Данный метод заключается в следующем.

Строится грузовая эпюра изгибающих моментов от всех внешних нагрузок, действующих на балку. В точке, прогиб которой определяется, прикладывается единичная сила Р=1 и строится единичная эпюра изгибающих моментов, возникающих в результате ее действия. Для определения прогиба сечения балки применяется формула Верещагина:

∆= ,

где ω_р- площадь грузовой эпюры изгибающих моментов;

_с - ордината единичной эпюры, соответствующая центру тяжести грузовой эпюры;

Е - модуль Юнга материала балки (модуль упругости І рода);

І_ос- осевой момент инерции поперечного сечения балки.

Методика определения угла поворота сечения балки аналогичная описанной, за исключением того, что в сечении угол поворота которого определяется, прикладывается единичный момент = 1.

Применим метод Верещагина для определения прогиба и угла поворота сечения балки, рассматриваемой в данной работе. А именно, определим прогиб точки С и угол поворота D (см. рис. 4.1).

После построения грузовой М и единичных _i эпюр (от действия соответственно единичной силы = 1, приложенной в точке С, и единичного момента = 1, приложенного в точке D), используем формулу (4.1.).

Для определения прогиба точки С она примет вид:

Δс= = ( _с1·ω_р1+ _с2 ω_р2) = (а²+ ). (4.1)

Для определения угла поворота сечения D формула выразится:

Θ_D= = ( _c1·ω_р1+ _с2 ω_р2)= (а²+ ). (4.2)

Таким образом после подстановки в формуле (4.1) и (4.2) значений Е, Р и размеров балки, мы получим величины прогиба Δс и угла поворота Θ_D.

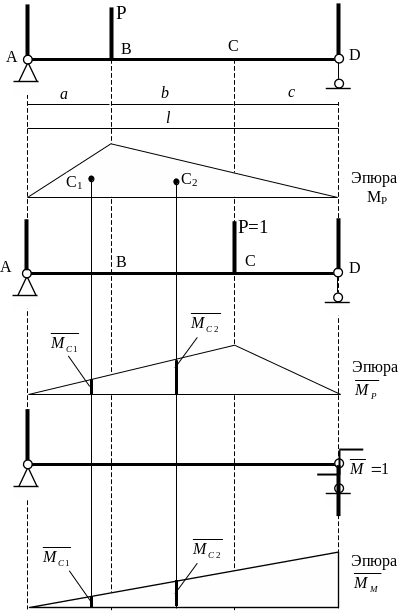
Рис. 4.1

Установка для проведения опыта (рис. 4.2) представляет собой стальную балку 1 прямоугольного поперечного сечения, расположенную на двух опорах. Для нагружения балки в любой точке служит передвижная подвеска 2, на которую кладутся гири. При этом замеры прогибов балки в нужной точке производится индикатором 3, закрепленном на передвижном штативе 4. Для определения углов поворота крайних сечений балки в этих точках предусмотрена возможность измерения поворота сечения с помощью индикатора 5 по схеме, изображенной на рис. 4.3. В результате угол поворота сечения определится из выражения:

tgΘ  Θ = Δ_D^гор / h_D (4.3)

где Δ_D^гор.- показания индикатора 5, мм; h_D= 150 мм.

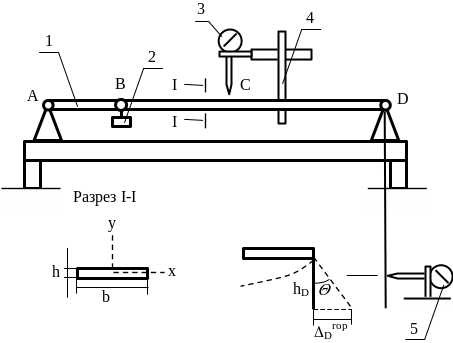
Рис. 4.3

Порядок проведения работы.

1. Измерить необходимые размеры балки: b, h, l, а, b, с.

2. Установить в точке В подвеску с начальным грузом Р_о = 0,5 кг. Показания индикаторов, при этом, выставить на нули.

3. Постепенно добавляя гири, ступенчато увеличивать нагрузку с шагом ΔР=1кг(=10Н).

4. После каждого увеличения нагрузки снимать показания индикаторов и результаты заносить в таблицу.

5. Определить величины прогибов ∆с_і и ∆D_i:

Δc_i=u_i⁽³⁾ – u_i-1⁽³⁾, Δ_Di^гор = u_i⁽⁵⁾ – u_i-1⁽⁵⁾,

где u_i⁽³⁾ , u_i⁽⁵⁾- показания индикаторов 3 и 5 после і - того опыта.

6. Определить средние величины ∆с и D^гор.:

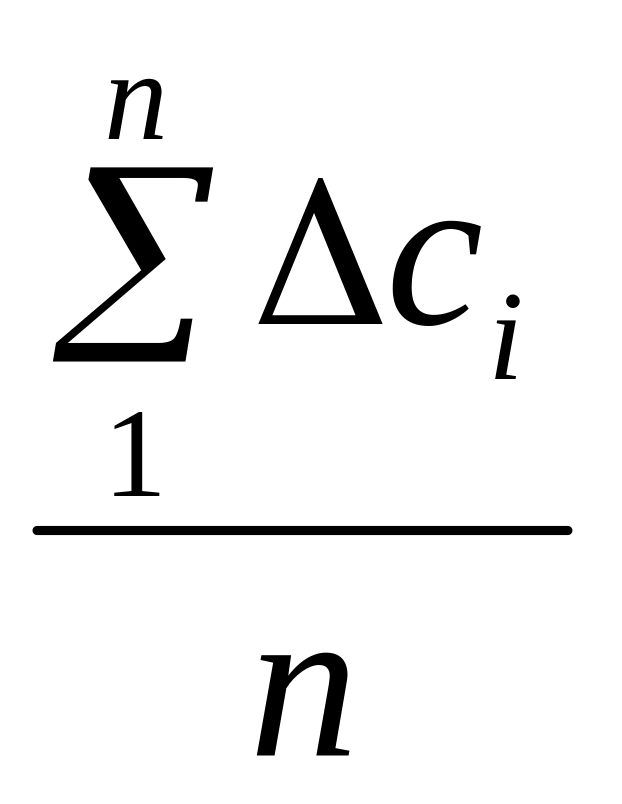с= , D^гор= ,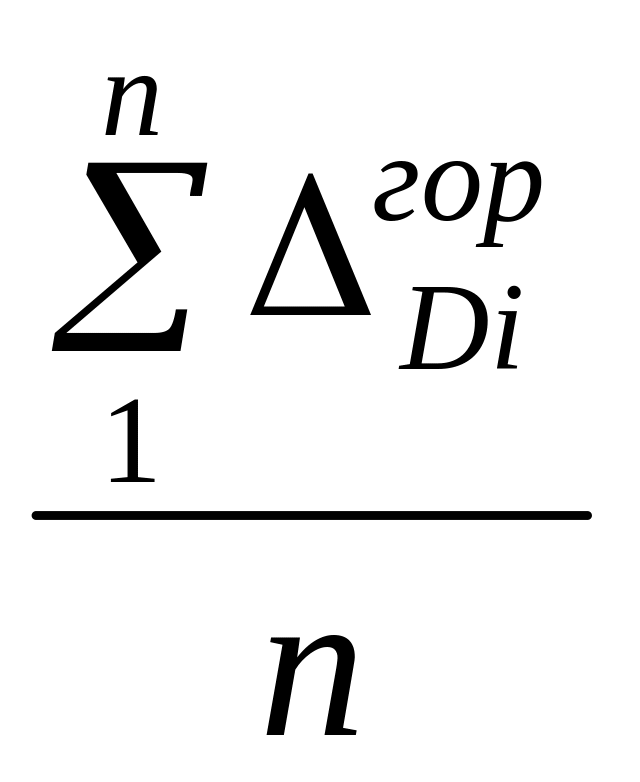

где n - число опытов.

7. Записать опытные величины прогиба сечения и угла поворота сечения D:

Δс_оп= с, Θ_Don=

8. Используя формулы (4.1) и (4.2) определить теоретические значения Δс_т и Θ_Dт при Р = 10Н и сравнить их с опытными.

Содержание отчета.

1. Название и цель работы.

2. Теоретические предпосылки (по желанию).

3. Результаты измерений и вычислений, выполненных согласно раздела 5.

4. Итоговая таблица.

5. Выводы по работе.

Контрольные вопросы.

1. Какие способы определения прогибов при изгибе балки Вы знаете?

2. Каковы пределы применимости формул для определения прогибов и углов поворота сечений при изгибе?

3. Запишите формулу Верещагина.

4 Объясните отличие применения метода Верещагина при определении прогиба, с одной стороны, и угла поворота сечения балки, с другой.

№ опыта	Рi, кг	ΔРi, кг	ui(3), мм	Δсi, мм	ui(5), мм	ΔDiгор, мм
0	0,5	0	0	0	0	0
1	1,5	1
2	2,5	2
3	3,5	3