2.Вимірювальна установка

Для вимірювання абсолютних рівней напруги, струму і потужності на опорі Z збирається схема, зображена на рис. 1.

В якості генератора в роботі використовується будь-який генератор тональної частоти з внутрішнім опором R₀ = 600 Ом, від якого можна отримати струм частотою f = 800 Гц.

Рис.1

Показник рівня (ПР) взагалі має два входи – високоомний і низькоомний (R₀=600 Ом). У цій роботі потрібно використовувати тільки високоомний вхід.

В якості опору використовується набір опорів або магазин опорів, на якому встановлюються наступні опори:

|Z| = 100, 200, 400, 600, 800, 1000 і 1400 Ом.

3.Порядок виконання роботи

1. Ознайомитися з конструкцією і схемами вмикання генератора частоти і ПР.

2. Відградуювати показник і встановити на генераторі f = 800 Гц.

3. Зібрати вимірювальну схему згідно з рис. 1, включивши замість опору Z магазин опорів або набір опорів.

4. Для кожного Z, вказаного в п.2, виміряти ПР абсолютні рівні напруги.

5. Для кожного значення Z визначити абсолютні рівні струму і потужності за формулами (9) і (11), а також значення напруги на опорі Z за формулою (12).

6. Розрахувати, якому струму і якій потужності відповідають отримані значення абсолютних рівнів щодо струму і потужності.

7. За виміряними і обчисленими даними побудувати в одних координатних осях графіки функцій:

4.Склад звіту

У звіті по роботі необхідно представити:

а) схему вимірювальної установки;

б) дані вимірів і всі розрахунки;

в) графіки побудованих залежностей.

Результати вимірів і розрахунків заносяться в таблицю.

№ пп.	Значення |Z|; Ом	PU,		PI,		PS,			U, B	I, A	S, Вт
		Нп	дБ	Нп	дБ	Нп	дБ
1	2	3	4	5	6	7	8	9		10	11

5.Контрольні запитання

1. Що називається відносним рівнем?

2. Що називається абсолютним рівнем?

3. Які величини струму, напруги, опору і потужності прийняті за одиниці нульового рівня?

4. У яких одиницях вимірюються рівні?

5. Яким відношенням зв’язані непер і бел?

Лабораторна робота №2 Дослідження частотних характеристик двоелементних двополюсників

1.Теоретичні відомості

Будь-яке електричне коло, яке розглядають відносно двох зажимів, називається двополюсником. За характером елементів двополюсники поділяються на реактивні, які складаються з індуктивностей і ємностей, і двополюсники з втратами, які включають в себе активні опори. Реактивні двополюсники представляють собою ідеалізовані електричні системи, які наближаються за своїми властивостями до фізично реалізуємих кіл з малими втратами. Вони широко використовуються в електричних колах із спеціальними частотними характеристиками, особливо в фільтрах і вирівнювачах.

Частотною характеристикою реактивного двополюсника називають залежність його опору чи провідності від частоти. Частотні характеристики різних двополюсників мають цілий ряд загальних властивостей:

1. Кількість резонансних і антирезонансних частот у реактивних двополюсників на одиницю менше кількости елементів (резонансною називається така частота, при якій опір реактивної схеми дорівнює нулю, антирезонансною – частота, при якій опір наближається до нескінченності).

2. Резонансні і антирезонансні частоти в реактивному двополюснику чередуються.

3. З урахуванням знака реактивний опір двополюсника в діапазоні між найближчими антирезонансними частотами із збільшенням частоти збільшується.

4. При частоті, яка дорівнює нулю, опір реактивного двополюсника може наближатися до нуля (без урахування витрат) або до нескінченності, у залежності від характеру втрат при даній частоті; той же висновок дійсний і для частоти, яка наближається до нескінченності.

5. Якщо при ω = 0; Z(ω) = 0, то в даному реактивному двополюснику першою йде антирезонансна частота; якщо при ω = 0, Z(ω)→∞, то першою йде резонансна частота.

Наведені загальні властивості реактивних двополюсників дозволяють побудувати графіки частотних характеристик конкретних схем.

У даній роботі досліджуються двохелементні реактивні двополюсники – резонансний і антирезонансний контури, схема яких наведена на рис. 1.

Рис.1

У резонансний контур входять послідовно включені індуктивність L₁ і ємність C₁ і він має одну резонансну частоту ω₁, яка визначається наступним чином:

. (1)

Частотна характеристика резонансного контуру може бути визначена за допомогою формули

, (2)

де ω – поточна частота.

Антирезонансний контур складається з паралельно включеної індуктивності L₂ і ємності C₂ і має одну антирезонансну частоту ω₂:

. (3)

Частотна характеристика антирезонансного контуру визначається за допомогою наступної формули:

. (4)

Графіки частотних залежностей двоелементних двополюсників приведені на рис. 2 (а – для резонансного контуру, б – для антирезонансного контуру).

У реальних схемах реактивних двополюсників через втрати в елементах при резонансних і антирезонансних частотах Z(ω) не дорівнює нулю або нескінченності, а мінімально чи максимально відповідно. При цьому для резонансних частот Z(ω) практично дорівнює активним втратам в елементах.

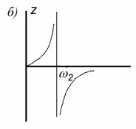
Рис.2