Правила приближенных вычислений

При решении физических задач числовые значения, с которыми приходится иметь дело, большей частью являются приближенными. Задачи с приближенными данными следует решать, учитывая правила приближенных вычислений.

Правила приближенных вычислений состоят в следующем.

1.Учитывать количество значащих цифр, необходимых для соблюдения определенной точности вычислений. Значащими называют все цифры, кроме нуля, а также нуль в двух случаях: а) когда он стоит между значащими цифрами; б) когда он стоит в конце числа и известно, что единицы соответствующего разряда в данном числе нет. Например:

1603 – 4 значащих цифры;

1,03 – 3 значащих цифры;

1,00 – 3 значащих цифры;

0,00103 – 3 значащих цифры.

3. Так как с помощью вычислений получить результат более точный, чем исходные данные невозможно, то достаточно производить вычисления с числами, содержащими не более знаков, чем в исходных данных.

4. При сложении или вычитании приближенных чисел, имеющих различную точность, более точное должно быть округлено до точности менее точного. Например:

9.6 + 0.176 = 9.6 + 0,2 = 9.8

100,8 – 0,427 = 100,8 –0.4 = 100.4

5. При умножении и делении следует в полученном результате сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством значащих цифр. Например:

0.637  0.023 = 0.0132 но не 0.0132496;

6. : 3 = 2 но не 2.107.

7. При возведении в квадрат или куб нужно сохранять столько значащих цифр, сколько их имеет возводимое в степень число. Например:

1.25² = 1.56, но не 1.5625;

1.01³ = 1.03, но не 1.030301 .

8. При извлечении квадратного и кубического корней в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число. Например:

10^1/2 = 3.1, но не 3.162 ;

10^1/3 = 2.1, но не 2.154.

9. При вычислении сложных выражений соблюдаются правила в зависимости от вида производимых действий.

10. Когда число мало отличается от единицы, можно пользоваться ниже приведенными приближенными формулами.

Если a, b , c малы по сравнению с единицей (меньше 0.1), то:

(1a) (1b) (1c) = 1  a  b  c ;

(1a)^1/2 = 1 a/2 ; (1a)ⁿ = 1 n  a;

1/ (1a)ⁿ = 1  n  a;

е^а = 1+a; ln(1a) =a – a²/2;

Если угол меньше 5⁰ и выражен в радианах, то в первом приближении можно принять sin   tg  ; cos  1.

Соблюдая эти правила, студент сэкономит время на вычислениях при решении физических задач.

Методические указания

Основные законы и формулы механики

Скорость мгновенная v = dх/dt

Угловая скорость мгновенная  = d/dt

Ускорение :

мгновенное а = dv/dt = d²х/dt²

тангенциальное а_ = dv/dt

нормальное а_n = v²/r

полное a =  а_ ² + а_²

Угловое ускорение мгновенное  = d/dt = d²/dt²

Cвязь между линейными и угловыми s = r ; v = r ;

величинами, характеризующими движение а_ =  r ; а_n = ² r .

точки по окружности .

Второй закон Ньютона для поступательного d P/dt =  F_i

движения i

Второй закон Ньютона для поступательного m a =  F_i

движения тела с m =const i

Количество движения материальной точки P = mv

массы m, движущейся со скоростью v

Потенциальная энергия:

упругодеформированного тела (работа Е_пот = А = k х²/2 ;

упругой силы)

гравитационного взаимодействия двух тел Е_пот = -G m₁m₂/r ;

тела в однородном поле тяготения Е_пот = mgh .

Кинетическая энергия поступательного Е_кин = mv²/2 = P²/2m

движения тела

Момент инерции материальной точки J = mr²

массой m на расстоянии r от оси вращения

Моменты инерции некоторых тел массы m

относительно оси вращения проходящей

через центр тяжести:

полого цилиндра (колеса) радиуса R J = m R² ;

сплошного цилиндра (диска) радиуса R J = mR²/2 ;

шара радиуса R J = 0.4 mR² ;

стержня длиной l, если ось  стержню J = ml²/12 ;

тела относительно произвольной оси (тео- J = J₀ + md² .

рема Штейнера)

Момент силы относительно оси вращения М = [ r F ]

Момент количества движения L = J

Основное уравнение динамики вращательного M = d L/dt = d(J)/dt

движения твердого тела

то же для J = const M = J d/dt = J

Закон сохранения момента количества  J_i_i = const

движения

Кинетическая энергия вращающегося тела Е_вращ = J²/2

Закон сохранения энергии Е_пот +Е_кин +Е_вращ=const

Работа при повороте на угол d dА = Md

Основные законы и и формулы электростатики и постоянного тока.

Закон Кулона F = q₁ q₂ / 4₀ r²

Напряженность электрического поля Е = F/q₁

Напряженность поля точечного заряда q₂ Е = q₂ / 4₀ r²

Теорема Остроградского – Гаусса  Е_ndS = ( q_i )/ ₀

Cвязь между потенциалом  и напряженностью Е = -grad 

поля

Сила тока I = dq/dt

Заряд, прошедший по проводнику q =  I(t) dt

Закон Ома для замкнутой цепи I = / (R + r)

Закон Джоуля –Ленца для пост. Тока Q = I²R t

То же для тока, зависящего от времени Q =  I²(t)Rdt

Сопротивление однородного проводника R =  l /S

Полная мощность , выделяющаяся в цепи P = I  = ²/ (R + r )

Основные законы и формулы электромагнетизма

Закон Ампера dF = BidLsin

Механический момент, действующий на контур M = p_mB sin

с током помещенный в магнитное поле

Магнитный момент контура с током p_m = IS

Cвязь магнитной индукции с напряженностью В = ₀Н

магнитного поля

Магнитная индукция в центре кругового тока В = ₀I/2R

Магнитная индукция поля:

созданного бесконечно длинным B = ₀I/2R

проводникомс током на расстoянии R

созданного отрезком проводника с током B = ₀I(cоs₁ –cos)/4d

на расстоянии d

беконечно длинного соленоида и тороида В =₀ n I

имеющих плотность витков n

Cила Лоренца F = q E + q [v B]

Закон электромагнитной индукции Фарадея Е =- N dФ/dt

Потокосцепление  = NФ

Потокосцепление соленоида  = LI

Электродвижущая сила самоиндукции _s = - L dI/dt

Индуктивность соленоида длиной l L = ₀ n² lS

и сечением S

Объемная плотность энергии

электромагнитного поля

Связь между мгновенными значениями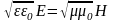

напряженностей электрического Е

и магнитного Н полей электромагнитной волны

Плотность потока электромагнитной энергии

вектор Умова – Пойтинга