
- •Варианты контрольных работ для студентов заочного отделения
- •1. Контрольная работа № 1
- •10. Темы и методические указания для контрольных работ студентов заочной формы обучения Указания о порядке выполнения контрольных работ
- •Правила приближенных вычислений
- •Методические указания
- •Примеры решения задач
Варианты контрольных работ для студентов заочного отделения
1. Контрольная работа № 1
Автомобиль начинает движение при включенном зеленом свете светофора. Зависимость пройденного пути от времени описывается уравнением S = 0,1t2 + 0,03 t3 [м].
Определить: 1) время t после начала движения автомобиля, через которое его ускорение а = 2 м/с2;
2) среднее ускорение < a > автомобиля за этот промежуток времени;
3) мгновенную скорость движения в этот момент времени.
Две материальные точки движутся согласно уравнениям:
X1 = 4 t + 9 t2 – 16 t3 [м];
X2 = 2 t – 4 t2 + 1,2 t3 [м].
Найти: 1) в какой момент времени ускорения этих точек будут одинаковы;
2) скорости точек в этот момент времени;
3) расстояния, пройденные точками за это время.
Автомобиль начинает движение при включенном зеленом свете светофора. Зависимость пройденного пути от времени описывается уравнением: S = 2 t – 3 t2 + 4 t3 [м].
Определить: 1) через сколько времени после начала движения ускорение автомобиля будет равно 1 м/с2;
скорость движения в этот момент времени;
расстояние, пройденное автомобилем за это время.
Движение сидения на карусели радиусом 4 м за первые 2 с движения задано уравнением S = 10 – 2 t + t2 [м].
Найти: 1) тангенциальное ускорение;
нормальное ускорение;
полное ускорение;
пройденное расстояние за это время.
Точка движется по окружности радиусом 2 см. Зависимость пути от времени задается уравнением X = 0,1 t3 [м].
Найти: 1) нормальное ускорение;
тангенциальное ускорение точки;
полное ускорение точки в момент времени 2 с после начала движения.
Движение сиденья на карусели радиусом 4 м задается уравнением: S = 8 – 2 t2 [м].
Найти: 1) момент времени, при котором нормальное ускорение сиденья будет равно 9 м/с2;
скорость в этот момент времени:
тангенциальное и полное ускорения в этот момент времени.
При растяжении алюминиевого стержня диаметром 3,88 мм и длиной 2,1 м он получил относительное удлинение 0,032. Модуль Юнга для алюминия Е = 69 ГПа.
Найти: 1) силу, приложенную к стержню;
2) работу, совершенную силой при растяжении стержня.
Человек, массой 82 кг, стоящий на краю горизонтальной платформы массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 мин -1, переходит к ее центру. Считая платформу круглым однородным диском, а человека точечной массой, определить, с какой частотой будет тогда вращаться платформа.
После удара молотком по алюминиевой заклепке длиной 2,2 см и диаметром 5 мм она получила относительное сжатие 0,02. Модуль Юнга для алюминия Е = 69 ГПа.
Найти: 1) силу, приложенную к заклепке;
работу, совершенную силой при сжатии заклепки.
Тяжелый камень брошен вверх с высоты 10 м под углом 450 к горизонту с начальной скоростью 5 м/с.
Найти: 1) общую продолжительность полета камня до соприкосновения с землей;
максимальную высоту подъема камня;
дальность полета камня.
Тело брошено параллельно поверхности земли со скоростью 10 м/с с высоты 12 м. Пренебрегая сопротивлением воздуха
Определить: 1) продолжительность полета тела до касания с землей;
дальность полета тела.
На земле стоит бочка с водой, в боковой поверхности которой имеется отверстие. Поперечное сечение отверстия значительно меньше поперечного сечения самой бочки. Отверстие расположено на расстоянии 64см ниже уровня воды, который поддерживается постоянным, и на расстоянии 25 см от дна бочки. При расчете вязкостью воды и сопротивлением воздуха пренебречь.
Найти: на каком расстоянии по горизонтали от бочки падает на поверхность струя воды, вытекающая из отверстия.
Определить собственную длину и массу стержня в неподвижной системе координат, если в движущейся системе со скоростью 240000 км/с его длина составляет 1,8 м, масса 240 кг, а угол между ним и направлением движения равен 450.
Длина ракеты, движущейся со скоростью 260000 км/с равна 186,3 м, а ее масса – 580000 тонн.
Определить длину ракеты и ее массу на земле до старта и полную энергию при движении.
Две ракеты, движущиеся со скоростями близкими к скорости света (о,8 с и 0,85 с) под углом друг к другу 600 имеют одинаковую массу 600000 тонн.
Определить массы ракет относительно неподвижной системы координат.
В сосуд, наполненный глицерином плотностью 1,2 г/см3 и вязкостью 1,6 Па с падает металлический шарик диаметром 1 мм (плотность стали 7,8 г/см3).
Найти время, за которое шарик достигнет дна сосуда, если высота уровня глицерина в нем 45 см.
В сосуд, наполненный отстоявшимся бензином (плотностью 0,75 г/см3) и водой (плотностью 1 г/см3) брошен стеклянный шарик диаметром 3 мм (плотность стекла 2,7 г/см3). Высота столба жидкости бензина 10 см, а воды 5 см, а отношение вязкостей 0,6.
Найти время падения шарика на дно сосуда.
Определить индукцию магнитного поля в центре проволочной квадратной рамки со стороной квадрата 15 см, если по рамке течет ток 5 А.
В катушке длиной 0,5 М и диаметром 5 см, число витков равно 1500 ток равномерно увеличивается на 0,2 А за секунду. На катушку надето кольцо из медной проволоки (удельное сопротивление меди 17 нОм*м) площадью сечения 3 мм2. Определить силу тока в кольце.
Кольцо радиусом 5 см из тонкой проволоки несет равномерно распределенный заряд 10 нКл. Определить потенциал электростатического поля в центре кольца.
Кольцо радиусом 5 см из тонкой проволоки несет равномерно распределенный заряд 10 нКл. Определить потенциал электростатического поля на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца.
На металлической сфере радиусом 15 см находится заряд Q = 2 нКл. Определите напряженность Е электростатического поля: 1) на расстоянии
r1 = 10 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии r2 = 20 см от центра сферы.
Поле создано двумя равномерно заряженными концентрическими сферами радиусами R1 = см и R2 = 8 см. Заряды сфер соответственно равны Q1 = 2 нКл и Q2 = - 1 нКл. Определите напряженность электростатического поля в точках, лежащих от центра сфер на расстояниях: 1) r1 = 3 см; 2) r2 = 6 см; 3) r3 = 10 см.
Электростатическое поле создается положительно заряженной с постоянной поверхностной плоскостью q = 10 нКл/м2 бесконечной плоскостью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния r1 = 2 см до r2 = 1 см ?
Сила тока в проводнике сопротивлением R =100 Ом равномерно убывает от I0 = 10 до I= 0 за время τ = 30 с. Определите выделившееся за это время в проводнике количество теплоты.
Сила тока в проводнике сопротивлением R =120 Ом равномерно возрастает от I0 = 0 до Iмакс= 5 А за время τ = 15 с. Определите выделившееся за это время в проводнике количество теплоты.
В плоский конденсатор, расстояние между пластинами которого 5 мм, вдвигают стеклянную платину с диэлектрической проницаемостью ε = 7 с постоянной скоростью 50 мм/с. Ширина пластины 4,5 мм, ЭДС батареи 220 В. Определите силу тока в цепи батареи, подключенной к конденсатору.
Два источника тока с ЭДС 2 В и 1,5 В и внутренними сопротивлениями r1 = 0,5 Ом и r2 = 0,4 Ом включены параллельно сопротивлению R =2 Ом. Определить силу тока через это сопротивление.
Тонкое кольцо массой 10 г и радиусом 8 см несет заряд, равномерно распределенный с линейной плотностью 10 нКл/м. Кольцо равномерно вращается с частотой 15 с-1 относительно оси, перпендикулярной плоскости кольца и проходящей через ее центр. Определить магнитный момент pm кругового тока, создаваемого кольцом.
Тонкое кольцо массой 10 г и радиусом 8 см несет заряд, равномерно распределенный с линейной плотностью 10 нКл/м. Кольцо равномерно вращается с частотой 15 с-1 относительно оси, перпендикулярной плоскости кольца и проходящей через ее центр. Определить отношение магнитного момента pm к моменту импульса кольца.
Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного провода, в точке, равноудаленной от концов отрезка и находящейся на расстоянии 4 см от его середины. Длина отрезка провода 20 см, а сила тока в проводе 10 А.
Определить магнитную индукцию В поля в центре проволочной квадратной рамки со стороной 15 см, если по рамке течет ток 5 А.
Мост Уитстона имеет значения сопротивлений R1 = 60 Ом, R2 = 40 Ом, R3 = R4 = 20 Ом, сопротивление гальванометра, RG = 100 Ом. Напряжение источника тока составляет 2 В. Определить силу тока, протекающего через гальванометр. Сопротивлением источника тока пренебречь.
Вольтметр, включенный в сеть последовательно с сопротивлением R1, показал напряжение 180 В, а при включении последовательно с сопротивлением R2 = 2R1 показал 168 В. Определить сопротивление R1 и напряжение в сети, если сопротивление вольтметра 1000 Ом.
К пластинам плоского воздушного конденсатора приложена разность потенциалов 500 в. Площадь пластин 200 см2, расстояние между ними 1,5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли парафин (ε = 2). Определить разность потенциалов между пластинами после внесения диэлектрика.
К пластинам плоского воздушного конденсатора приложена разность потенциалов 500 в. Площадь пластин 200 см2, расстояние между ними 1,5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли парафин (ε = 2). Определить емкости конденсаторов до и после внесения диэлектрика.
Трансформатор с коэффициентом трансформации 0,15 понижает напряжение с 220 В до 6 В. При этом сила тока во вторичной обмотке равна 6 А. Пренебрегая потерями энергии в первичной обмотке, определить сопротивление вторичной обмотки трансформатора.
Автотрансформатор, понижающий напряжение с 6 кВ до 220 В, содержит в первичной обмотке 2000 витков. Сопротивление вторичной обмотки 12 Ом. Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке трансформатора.
Катушку индуктивностью 0,6 Гн подключают к источнику тока. Определить сопротивление катушки, если за время 3 с сила тока через катушку достигает 70% предельного значения.
Электрическая схема состоит из параллельно соединенных трех сопротивлений, последовательно соединенного с ними амперметра. Амперметр показывает ток 1,5 А. Сила тока через сопротивление R1 равно 0,5 А. Сопротивления R2 = 2 Ом, R3 = 6 Ом. Определить сопротивление R1 , силу тока через сопротивление R2 и R3 .
В контуре АВСD э.д.с. ε1 = 2,0 В, ε2 = 1,8 В, резисторы R1 = 40 Ом, R2 =15 Ом и R3 = 10 Ом. Найти токи во всех участках цепи.
ε2 R1
R3
D C
|
|
|
|
Определить магнитный поток сквозь площадь поперечного сечения катушки (без сердечника), имеющей на каждом сантиметре длины n=8 витков. Радиус соленоида r =2см, сила тока в нём I=2А.
Два элемента имеют э.д.с. ε1=2В и ε2=4В, резистор R1=0,5 Ом.
Падение потенциала на резисторе R2 равно U2=1В. Найти показания Амперметра. |
|



А N D
R1 R3
R2
B ε1 M I2 C
|
Катушка длиной l=20см и диаметром D=3см имеет N=400 витков.
По катушке идёт ток I=2А. Найти индуктивность L катушки и магнитный поток Ф = LI, пронизывающий площадь её поперечного сечения.

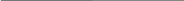


 A
B
A
B


 ε1
ε1


 R2
R2

 А
ε2
А
ε2


