3.3. Примеры статических и астатических систем

Как уже отмечалось, статизм автоматических систем определяется их внутренней структурой, поэтому попробуем разобраться в причинах, вызывающих эти свойства, и сделаем это на примерах систем стабилизации. В качестве объектов регулирования в этих системах использованы машины постоянного тока независимого возбуждения.

3.3.1. Автоматические системы стабилизации напряжения

1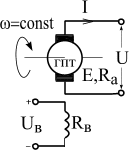 . Объект регулирования (рис.3.2). Объектом регулирования является генератор постоянного тока, для которого справедливо уравнение

,

где – активное сопротивление цепи якоря. Зависимость называется внешней характеристикой генератора и является одной из его статических характеристик. Согласно (3.4) статизм этой характеристики больше нуля

. Рис.3.2

Это означает, что по внешней характеристике генератор относится к устройствам статического типа.

2. Система стабилизации напряжения «статическая» (рис.3.3). Система имеет управляющее устройство, состоящее из источника регулируемого эталонного напряжения , усилителя, измерительного устройства в виде потенциометра R и цепи обратной отрицательной связи.

Когда под действием какого либо фактора изменяется выходное напряжение U, изменяется и величина ошибки регулирования . Пусть, например, произошло уменьшение U, тогда при отрицательной ОС рассогласование (ошибка) увеличится, и в системе произойдут следующие изменения: увеличится ток возбуждения , следовательно, увеличится э.д.с. якоря, и увеличится напряжение на зажимах генератора.

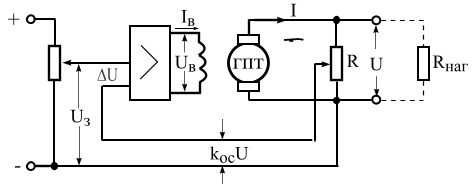
Рис. 3.3

Количественную оценку процесса регулирования сделаем с помощью математической модели системы, которая представляется следующей группой уравнений:

уравнение замыкания системы

(3.5)

уравнение усилителя с коэффициентом усиления

(3.6)

уравнение цепи обмотки возбуждения с сопротивлением

(3.7)

уравнение э.д.с. генератора

(3.8)

уравнение цепи якоря генератора

(3.9)

Совместное решение уравнений (3.5 -3.9) дает все возможные статические характеристики автоматической системы, некоторые из которых рассмотрим ниже.

Статическая ошибка регулирования . Для получения этой характеристики за независимую переменную примем I, за зависимую переменную примем , после исключения остальных переменных получим

.

Ошибка регулирования в установившемся режиме системы определится уравнением

(3.10)

где – коэффициент усиления разомкнутой системы. Это уравнение показывает, что увеличением коэффициента усиления k ошибку регулирования можно сделать сколь угодно малой, но ее полное исчезновение принципиально невозможно. Этот вывод можно сделать и из принципа действия системы: действительно, напряжение на обмотке возбуждения генератора не может существовать без сигнала рассогласования на входе усилителя, то есть в этой системе ошибка регулирования является фактором, обеспечивающим ее работоспособность.

Статическая внешняя характеристика системы . Решение системы уравнений относительно переменных U и I дает уравнение

(3.11)

где – напряжение системы в режиме холостого хода,

, .

Статизм системы. Этот параметр системы определяется согласно (3.3) с использованием внешней характеристики (3.11)

(3.12)

Статизм внешней характеристики системы. Подставляя в (3.4) значения напряжения системы по (3.11) при холостом ходе и при номинальной нагрузке , получим

. (3.13)

3. Система стабилизации напряжения «астатическая» (рис.3.4). Принципиальным отличием данной системы от предыдущей является использование в цепи управления исполнительного двигателя ИД, который и создает астатизм. Когда в системе рассогласования нет и напряжение на исполнительном двигателе равно нулю, движок потенциометра П неподвижен. Но при любом изменении напряжения генератора появляется рассогласование , которое заставляет исполнительный двигатель ИД вращаться. При правильном включении цепи обратной связи (это должна быть отрицательная ОС) движок потенциометра будет перемещаться в сторону, уменьшающую рассогласование. Вращение двигателя прекратится при исчезновении напряжения на его якоре, то есть при

Рис.3.4