7.2. Косвенные методы оценки качества регулирования

Метод распределения корней. Этот метод дает возможность приближенно оценить характер переходного процесса по расположению корней относительно мнимой оси. В основу метода положена идея оценки переходного процесса по тому корню характеристического уравнения, который ближе других расположен к мнимой оси. Этот корень может быть как вещественным , так и комплексно сопряженным .

Известно, что для системы с характеристическим уравнение n-го порядка

затухание переходного процесса определяется уравнением

,

в котором последней будет затухать составляющая с минимальной вещественной частью корня. Тогда, если отбросить влияние остальных корней, то порядок дифференциального уравнения системы снизится до первого порядка, если наименьший корень вещественный или до второго при минимальном комплексном корне.

Пусть самый опасный корень системы имеет вещественную часть , тогда потребовав, чтобы регулируемая величина за время регулирования уменьшилась в m раз, можно написать

.

После логарифмирования получим

.

Метод интегральных оценок. Если прямые показатели качества регулирования характеризуют отдельные его стороны, то интегральная оценка характеризует качество регулирования одним показателем. Но сложный динамический процесс не всегда удается однозначно характеризовать одним параметром, поэтому вводится понятие нескольких видов интегральных оценок.

Все виды интегральных оценок основаны на анализе ошибки регулирования

(7.2)

и любая интегральная оценка представляет собой интеграл от некоторой функции, связанной с этой ошибкой

. (7.3)

Простейшей интегральной оценкой является интеграл от мгновенного значения ошибки, то есть

. (7.4)

Э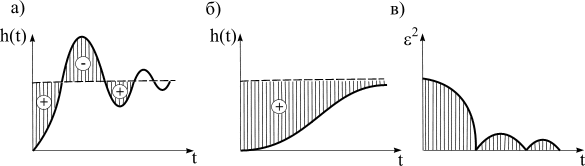 тот интеграл определяет заштрихованную площадь на рис. 7.3,а,б которая называется площадью регулирования. Однако такая оценка может применяться только для систем без перерегулирования, когда ошибка не меняет своего знака (рис. 7.3,б).

Рис. 7.3

Большее практическое значение имеет квадратичная интегральная оценка

, (7.5)

которая не зависит от знака ошибки. Интеграл определяет заштрихованную площадь на рис. 7.3,в, которую называют квадратичной площадью регулирования. Величина интеграла будет тем меньше, чем меньше сумма заштрихованных площадей, то есть чем ближе переходный процесс к ступенчатому изменению регулируемой величины. Но при таком переходном процессе получается большая скорость процесса при подходе регулируемой величины к новому установившемуся значению, что вызывает большое перерегулирование. Поэтому при оценке по интегралу сильно колебательный процесс иногда может оказаться лучше, чем апериодический, а это не всегда правильно.

Квадратичную интегральную оценку можно улучшить, если учесть не только ошибку, но и скорость ее изменения. Такая оценка дается интегралом

. (7.6)

В практике используются и более сложные интегральные оценки, в которых учитывается не только ошибка, но и ее первая, вторая и более высокие производные.

Ч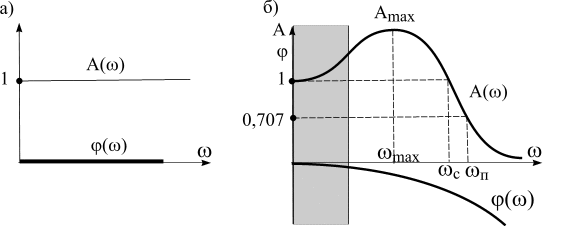 астотные методы. Рассмотрим сначала идеальную систему, в которой все элементы безынерционны. В такой системе выходной сигнал в любой момент времени точно копирует входной, и передаточная функция такой системы . Это означает, что амплитудно-частотная и фазо-частотная характеристики соответственно равны А() =1; () = 0. Они изображены на рис. 7.4,а.

Рис. 7.4

Но все реальные системы инерционны, и поэтому их частотные характеристики обычно имеют вид, приведенный на рис. 7.4,б. В реальных системах условия, близкие к идеальным, соблюдаются лишь на небольшом участке малых частот (он заштрихован на рис. 7.4,б). На резонансной частоте амплитуда имеет максимум , а при дальнейшем увеличении частоты резко падает. Это происходит потому, что система, вследствие своей инерционности, не успевает реагировать на колебания. Фаза выходного сигнала все более и более отстает от фазы входного сигнала, что отмечается уходом фазо-частотной характеристики в область отрицательных значений.

Для описания АФЧХ вводят следующие понятия:

Показатель колебательности - . Чем больше этот показатель, тем более колебательным является переходный процесс. При малых М система “вялая” и имеет большое время регулирования, а при больших М увеличивается перерегулирование, и система приближается к границе устойчивости. Обычно принимают

Частота резонанса частота, при которой амплитуда вынужденных колебаний достигает максимального значения.

Частота среза системы вычисляется на уровне . Она определяет диапазон частот вынужденных колебаний, которые пропускаются системой без ослабления. С увеличением увеличивается быстродействие системы, и увеличивается спектр входного сигнала, который система передает без искажений.

Полоса пропускания системы - вычисляется на уровне . С увеличением возрастает быстродействие системы.

Таким образом, М, , являются косвенными показателями качества переходного процесса, и эти параметры часто служат исходными данными при проектировании автоматических систем.