6.3. Методы определения устойчивости

Для того, чтобы система была устойчивой, должны выполняться определенные условия, которые называются условиями устойчивости. Все условия устойчивости разделяются на необходимые и достаточные.

Н е о б х о д и м о е условие устойчивости. Если это условие соблюдено система может быть как устойчивой, так и неустойчивой если же условие не соблюдается, то система наверняка неустойчива, и продолжение исследований на устойчивость теряет смысл. Хотя это условие не дает ответа на вопрос “устойчива система или нет”, оно позволяет на начальном этапе работ исключить заведомо непригодные варианты. Поэтому при исследовании устойчивости сначала проверяют соблюдение необходимого условия. Необходимым условием устойчивости системы является положительность всех коэффициентов ее характеристического уравнения. При этом равенство нулю хотя бы одного коэффициента также является нарушением необходимого условия.

Например, для системы с характеристическим уравнением

необходимое условие удовлетворяется, и исследование ее на устойчивость должно быть продолжено. А вот системы с характеристическими уравнениями

,

заведомо неустойчивы, так как в первой системе один коэффициент равен нулю, а во второй имеется отрицательный коэффициент.

Д о с т а т о ч н о е условие устойчивости. Это условие дает однозначный ответ на вопрос об устойчивости системы, если известны значения всех корней.

Достаточным условием устойчивости системы является отрицательное значение вещественной части всех корней ее характеристического уравнения.

Но, к сожалению, вычисление корней уравнений высоких степеней настолько сложно, что для исследования устойчивости предпочитают использовать специальные методы косвенных оценок. Эти методы позволяют оценить устойчивость системы по коэффициентам ее характеристического уравнения без вычисления корней. Такие оценки носят название “критерии устойчивости”.

6.4. Критерии устойчивости

Все критерии устойчивости делятся на алгебраические и частотные. Если для работы с алгебраическими критериями необходимо иметь, по крайней мере, характеристическое уравнение системы, то при использовании частотных критериев не обязательно иметь даже характеристическое уравнение, так как устойчивость может быть определена по экспериментальным характеристикам. Это свойство частотных критериев широко используется в практике работы со сложными системами, такими, например, как энергетические системы, когда построение математической модели затруднено. К алгебраическим критериям относятся критерии Гурвица и Рауса, к частотным - критерии Найквиста и Михайлова.

Критерий Гурвица. Проверка устойчивости по Гурвицу сводится к вычислению n определителей, которые составляются по следующему правилу:

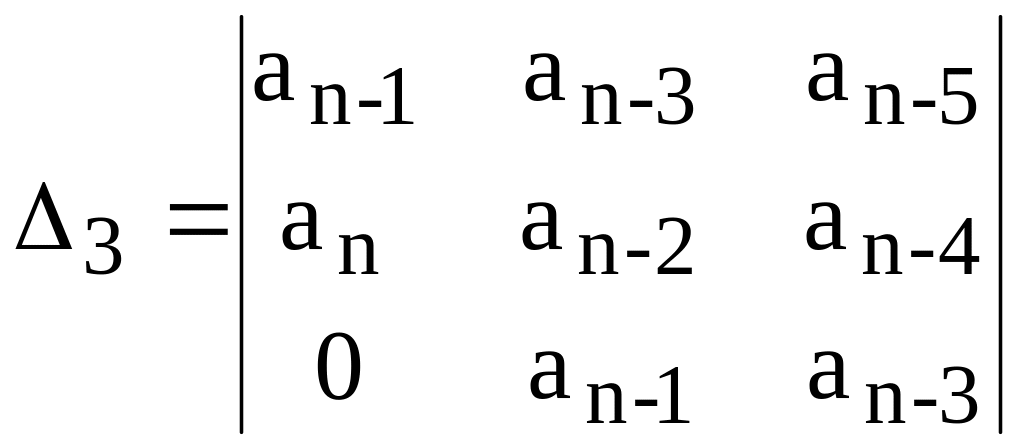; ; ; . . . (6.7)

По этому критерию система будет устойчивой, если все определители положительные.

Критерий Михайлова. Если в характеристическом уравнении системы заменим оператор p на j, получим функцию комплексного переменного

, 6.8)

которая в комплексной плоскости определяет вектор

. (6.9)

Этот вектор имеет следующее свойство. При изменении  от 0 до этот вектор будет поворачиваться около начала координат против часовой стрелки, меняя одновременно и свою длину. При этом конец вектора описывает кривую со следующими свойствами: кривая начинается на вещественной оси при в точке с координатой и заканчивается в n-ом квадранте при , если отчет квадрантов вести против часовой стрелки. Этот вектор называют годографом Михайлова.

Согласно этому критерию линейная система n-го порядка будет устойчива, если годограф Михайлова охватывает начало координат и последовательно проходит n квадрантов, а в последнем квадранте уходит в бесконечность. Если годограф проходит через 0, то система находится на границе устойчивости.

Н

а)

б)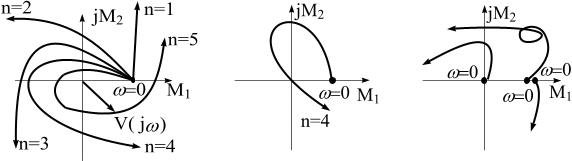

а рис. 6.3,а изображены годографы устойчивых систем с характеристическими уравнениями до пятой степени включительно. А на рис. 6.3,б приведены годографы неустойчивых систем.

К

Рис. 6.3

ритерий Найквиста. Этот критерий позволяет определить устойчивость системы по ее амплитудно-фазовым характеристикам, которые могут быть заданы как в аналитической форме, так и в виде опытных кривых. Особенностью критерия является то, что оценка устойчивости системы делается по характеристикам ее разомкнутого состояния. Это оказывается возможным благодаря однозначной зависимости между передаточной функцией разомкнутой системы и характеристическим уравнением этой системы в замкнутом состоянии.

Исследуемая система размыкается в любой точке, и аналитически или экспериментально определяется ее АФХ. Эта характеристика представляется комплексным уравнением . Устойчивость замкнутой системы определяется так:

1. если разомкнутая система устойчива или нейтральна, то для устойчивости замкнутой системы необходимо и достаточно, чтобы характеристика не охватывала точку с координатами (-1, j0);

2. если разомкнутая система имеет m корней с положительной вещественной частью, то замкнутая система будет устойчивой только в том случае, если характеристика охватывает точку (-1, j0) в положительном направлении 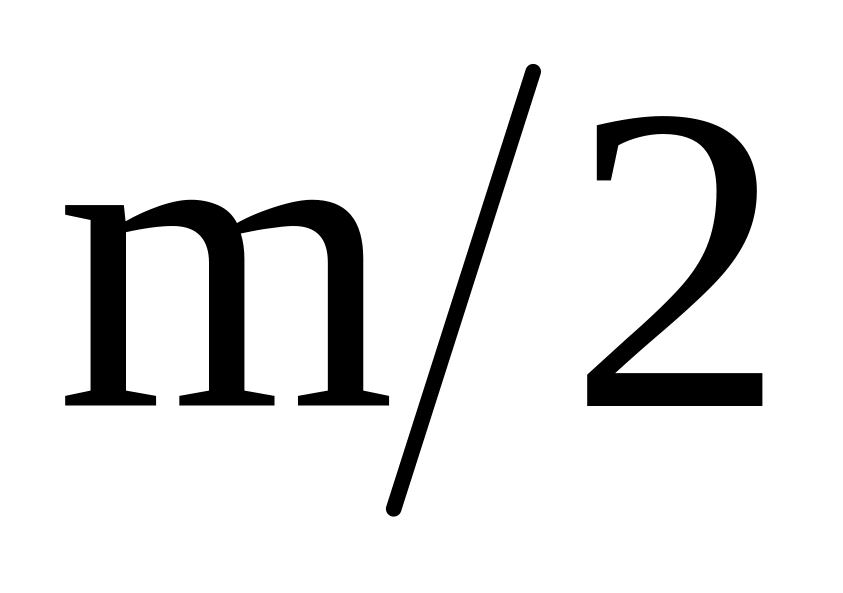раз.

Ф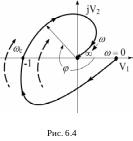 изическое объяснение этих условий можно дать с помощью рис. 6.4. Пусть при некоторой частоте система, находится на границе устойчивости. Это означает, что АФХ разомкнутой системы при этой частоте проходит через точку (-1, j0). Это означает также, что на данной частоте амплитуда выходного сигнала равна амплитуде входного сигнала, и они находятся в противофазе. Значит в замкнутой системе сигнал с выхода по цепи отрицательной обратной связи поступит на вход и будет точно равен по амплитуде и фазе входному сигналу. Если такую систему отключить от входного сигнала, ее состояние не изменится. В системе установятся незатухающие колебания, которые будут поддерживаться не за счет источника входного сигнала (он теперь отключен), а за счет энергии самой системы.

Если АФХ при частоте пересекает вещественную ось слева от точки (-1, j0), то есть охватывает эту точку, то амплитуда выходного сигнала на данной частоте больше входного и находится в противофазе. При замыкании системы амплитуда выходных колебаний будет возрастать, то есть система будет неустойчивой.

Если АФХ при частоте пересекает вещественную ось справа от точки

(-1, j0), то есть не охватывает ее, то амплитуда выходного сигнала на данной частоте меньше входного и находится в противофазе. В этом случае при замыкании системы амплитуда выходных колебаний будет затухать, то есть система будет устойчивой.