Глава 6 устойчивость автоматических систем
6.1. Понятие устойчивости
Под устойчивостью понимают способность системы самостоятельно приходить к установившемуся состоянию после приложения воздействия, которое вывело ее из состояния равновесия.
В качестве примера, иллюстрирующего устойчивость системы, может служить шарик на поверхности, движение которого тормозится трением (рис. 6.1).
Рис.6.1
Система называется устойчивой “в большом”, если она остается устойчивой при любых по величине начальных отклонениях ее координат. Иллюстрация такой устойчивости дана на рис. 6.1, а.
Система называется устойчивой “в малом”, если она устойчива только при ограниченных начальных отклонениях ее координат. Этому случаю соответствует рис. 6.1, б. Понятно, что система будет устойчива, пока начальные отклонения шарика находятся в пределах участка 1-2.
Система называется нейтральной, если она после снятия возмущающего воздействия хотя и приходит в состояние равновесия, но последнее может наступить при произвольном значении выходной координаты системы. Пример такой системы приведен на рис. 6.1, в.
Примером неустойчивой системы служит шарик на выпуклой поверхности (рис. 6.1, г). Малейшее отклонение шарика в любую сторону приведет к его скатыванию вниз.
Всегда ли за исходное состояние системы, устойчивость которой оценивается, берут состояние покоя? Нет, не всегда. В общем случае можно говорить об устойчивости движения вообще, то есть об устойчивости любого перемещения массы или энергии. Например, можно оценивать устойчивость движения спутника как его способность возвращаться на исходную орбиту после прекращения действия сил, отклонивших его от заданной орбиту. Точно так же оценивается устойчивость энергосистемы, параметры которой изменились при появлении в ней короткого замыкания, но должны восстановиться после его ликвидации.
Итак, мы рассмотрели качественную оценку понятия устойчивости, но существует также и количественная оценка устойчивости: устойчивость можно описать математически.
6.2. Устойчивость линейных систем
Свободное движение линейной системы описывается однородным дифференциальным уравнением
.
(6.1)
Решение этого уравнения представляется суммой экспонент
,
(6.2)
где
– корни
характеристического уравнения
.
(6.3)
В
Рис. 6.2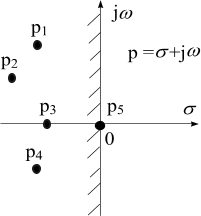
устойчивой системе величина xсв(t)
с течением времени должна стремиться
к нулю. Но это возможно только в том
случае, если все корни характеристического
уравнения будут либо отрицательные
действительные величины, либо комплексные
величины с отрицательной действительной
частью. Это означает, что для устойчивой
системы все корни должны располагаться
слева от мнимой оси комплексной плоскости
(рис.6.2). Превращение устойчивой системы
в неустойчивую произойдет в том случае,
если хотя бы один корень перейдет из
левой полуплоскости в правую. Границей
перехода является мнимая ось, которую
называют также границей
устойчивости системы.
Система может попасть на границу устойчивости несколькими путями .
1. Система имеет один нулевой корень. Если один корень характеристического уравнения будет лежать в начале координат, а все остальные корни – в левой полуплоскости, то такая система будет нейтральной. Действительно, в этом случае уравнение (6.2) станет таким
,
(6.4)
то есть после снятия возмущения состояние равновесия наступит, но оно наступит с неопределенной выходной координатой. Следует заметить, что при появлении уже второго нулевого корня система теряет устойчивость, так как решением (6.2) становится функция
.
(6.5)
2. Система имеет пару чисто мнимых
корней. Это означает, что корни попали
на мнимую ось (
)
и слагаемое, определяемое ими в (6.2),
представляет собой незатухающее
колебание с постоянной амплитудой
.
(6.6)
Такая граница устойчивости называется колебательной.
3. Система имеет бесконечный корень. Если в первых двух случаях корни попадали из левой полуплоскости в правую, пересекая мнимую ось, то в этом случае корень попадает в правую полуплоскость через бесконечность. Этот случай в практике встречается редко, и в дальнейшем нами рассматриваться не будет.